Добавлен: 09.01.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
(СПбГУТ)
Факультет Информационных систем и технологий
Кафедра Безопасности информационных систем
Отчет
По предмету «Алгоритмы и структуры данных»
о практической работе №2:
«Понятие рекурсии. Рекурсивные функции»
Выполнил студент гр. ИСТ-022:
Волков Кирилл
 // //
// //оценка
Проверил: Бородянский Ю.М.
 // //
// //Подпись
Задача работы
Изучить понятия рекурсии, рекурсивные функции в программировании, научиться применять рекурсивные методы в решении задач на языке С++, разработать программу по вычислению суммы кубов цифр числа и доказать, что, независимо от входного числа, результат работы программы сводится к числу 153. Приобрести навыки и умения анализа алгоритма и всего кода разработанной программы в Big-O-нотации.
Ход работы
Суть разработанного алгоритма: на входе даётся число, далее проверяется условие кратности трём, затем в случае «true», вызывается рекурсивная функция с вычислением суммы кубов цифр полученного числа, до тех пор, пока число не будет равно 153.
Блок-схема
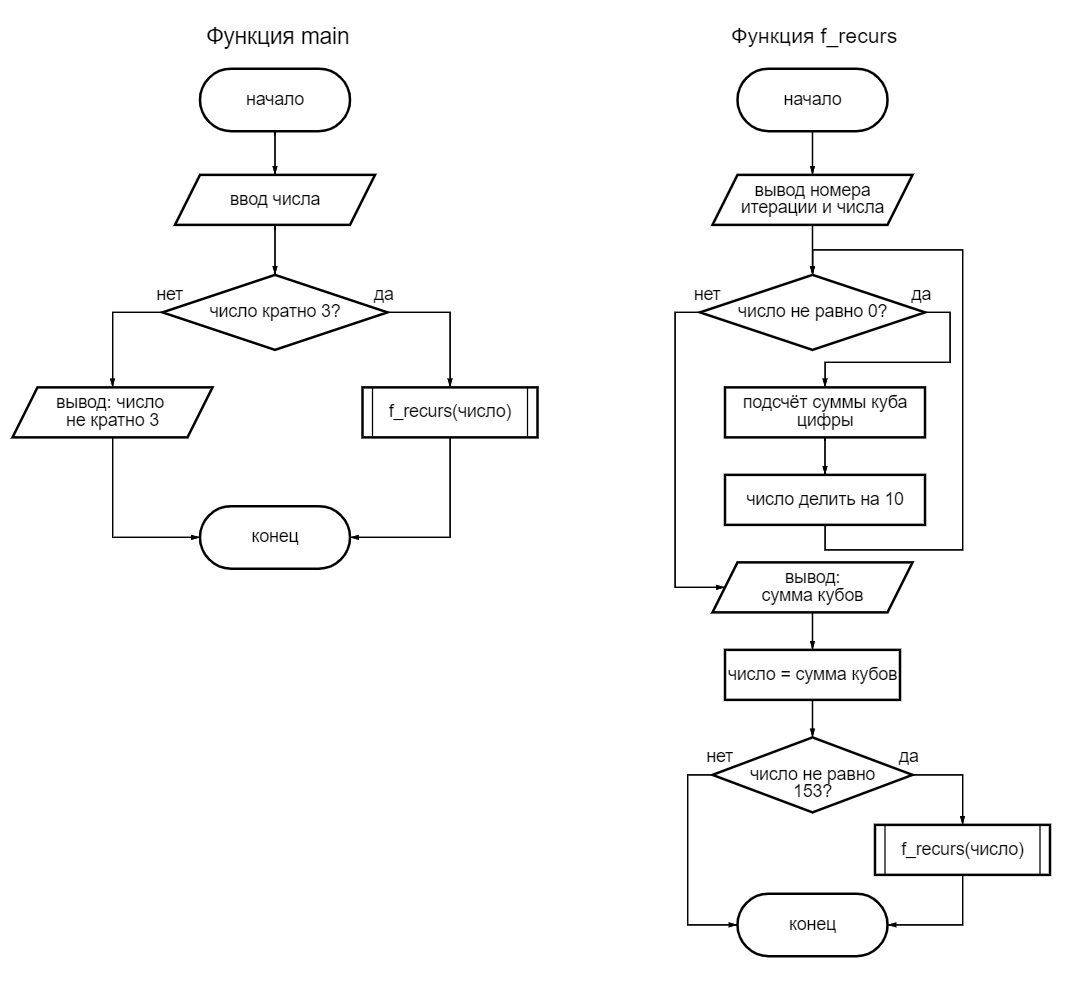
Рассчет сложности Big-O

Ответ: общая сумма сложности двух функций O(1) + O(n^2) = O(n^2)
Рекурсивная триада:
Параметр: число( numb )
База рекурсии: 1305
Декомпозиция: два цикла while
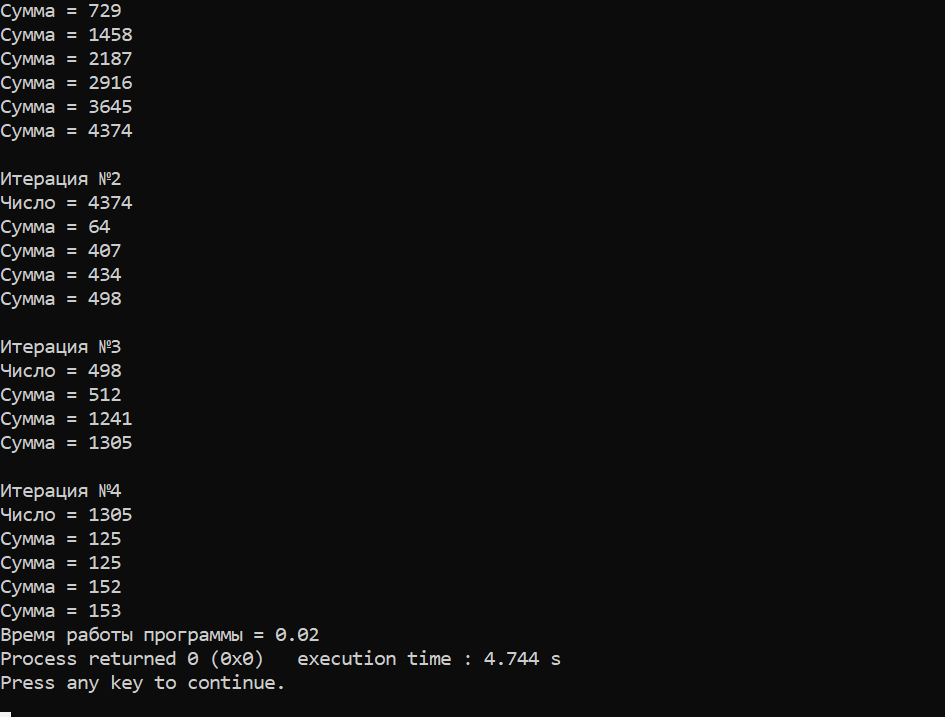
Результат работы программы
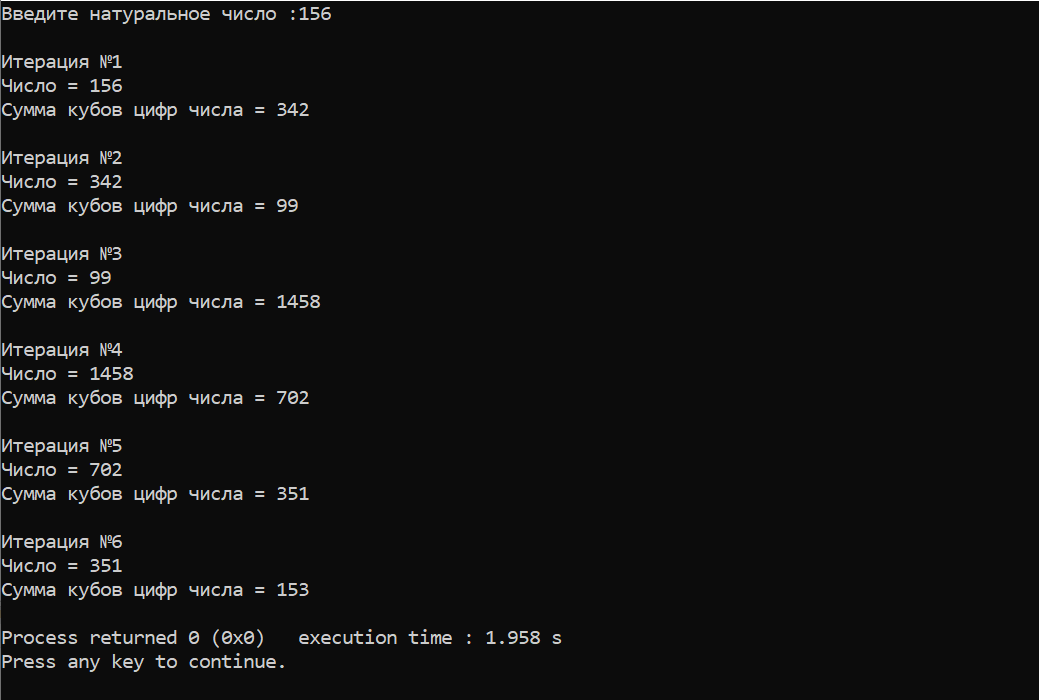
Время работы с рекурсией
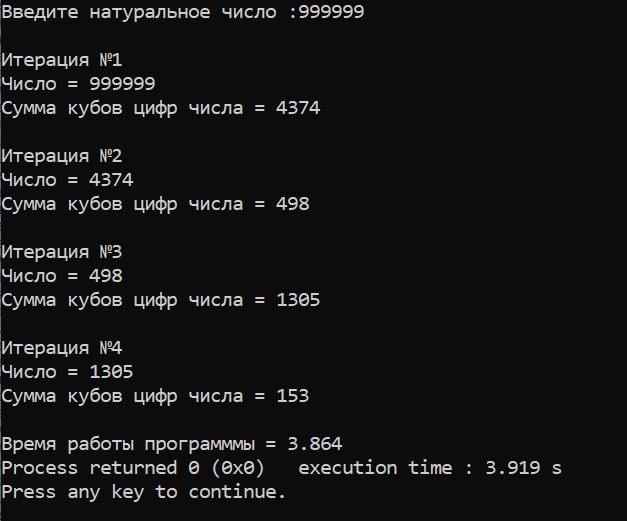
Время работы линейного алгоритма
Вывод
В результате работы была разработана программа, которая вычисляет сумму цифр куба числа, а затем повторяет вычисление с полученной суммой, и доказывает, что любое число при таком алгоритме сводится к 153.
На практике были применены знания о рекурсивных функциях.
В результате вычислений разных чисел, не была выявлено конкретной зависимости количества итераций от числа. В большинстве случаев – чем больше число, тем больше итераций.
Была проведена работа по анализу программного кода и была вычислена сложность в нотации Big-O.
Код программы смотрите в приложении 1
Приложение 1
#include
#include
#include
using namespace std;
int count_ = 0;
int f_recurs(int numb){
int cube=0;
count_ += 1;
cout<<"\nИтерация №"<
while (numb != 0){
cube += (numb%10) * (numb%10) * (numb%10);
numb = numb / 10;
}
cout<<"\nСумма кубов цифр числа = "<
numb = cube;
if ( numb != 153)
f_recurs(numb);
return 0;
}
int main()
{
SetConsoleOutputCP(1251);
SetConsoleCP(1251);
int numb;
cout<<"Введите натуральное число :";
cin>>numb;
if(numb%3==0)
{
f_recurs(numb);
}
else
cout<<"Число не кратно трём";
return 0;
}


г. Санкт-Петербург
2021