Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования «Рязанский государственный радиотехнический университет имени В.Ф. Уткина»Кафедра «Вычислительная и прикладная математика»Отчет по лабораторной работе № 2Изучение методов рационального кодирования сообщенийпо дисциплине: «Теоретические основы информационных процессов»Выполнил:студент группы 143Ярошенко А.М.Проверил:доц. каф. ВПМФилатов И.Ю.Рязань 2023Цель работы: выполнить программное моделирование алгоритма поиска кодовых комбинаций и алгоритма кодирования методами Шеннона-Фано и Хаффмана.Задание (вариант №23): смоделировать дискретный источник сообщений нормального распределения при M(x) = 0, σ = 1 и определить по распределению вероятности алфавитов (цифры 0-9, кириллица и латиница, 1000 символов юникода).Листингпрограммы:from math import sqrt, pi, ceil, logimport numpy as npfrom random import randomfrom operator import itemgetterclass Node:def __init__(self, prob, symbol, left=None, right=None):self.prob = probself.symbol = symbolself.left = leftself.right = rightself.code = ''codes = dict()def calculate_codes(node: Node, val=''):newVal = val + str(node.code)if node.left:calculate_codes(node.left, newVal)if node.right:calculate_codes(node.right, newVal)if not node.left and not node.right:codes[node.symbol] = newValreturn codesdef huffman_encoding(seq: dict()):nodes = [Node(seq[symbol], symbol) for symbol in seq.keys()]while len(nodes) > 1:nodes = sorted(nodes, key=lambda x: x.prob)right, left = nodes[0], nodes[1]left.code, right.code = 0, 1newNode = Node(left.prob + right.prob, left.symbol + right.symbol, left, right)nodes.remove(left)nodes.remove(right)nodes.append(newNode)huffman_dict = calculate_codes(nodes[0])return huffman_dictdef shannon_fano_encoding(seq: dict(), code=""):left, right = {}, {}if len(seq) == 1:dict_contained_symbols_and_codes_shannon_fano[seq.popitem()[0]] = codereturnif sum(seq.values()) == 0:counter = 0for k, v in sorted(seq.items(), key=itemgetter(1), reverse=True):if counter < len(seq) / 2:left[k] = velse:right[k] = vcounter += 1else:for k, v in sorted(seq.items(), key=itemgetter(1), reverse=True): if sum(left.values()) < sum(seq.values()) / 2:left[k] = velse:right[k] = vshannon_fano_encoding(left, code + "0")shannon_fano_encoding(right, code + "1")def r():r = 0for _ in range(12):r += random()return r - 6

---

def random_value(n):return [SIGMA * r() + MX for _ in range(n)]def probabilities(array):delta = (np.max(array) - np.min(array)) / INTERVALresult = []iter = np.min(array)while abs(iter - np.max(array)) > EPS:result.append(len(array[(array >= iter) & (array < iter + delta)]) / N)iter += deltareturn resultdef encode_string(string, data: dict()):return [data[char] for char in string]def print_dict(data: dict(), string):file = open(string, "w", encoding="utf-8")for k, v in data.items():file.writelines(str(k) + " " + str(v) + "\n")file.close()#Параметры для закона нормального распределенияK = sqrt(8 / pi)MX = 0SIGMA = 1EPS = 1e-4N = 100_0000#Цифры# list_symbols = [str(i) for i in range(10)]#Символы из Юникода# list_symbols = [chr(i) for i in range(32, 1200 + 1)]#Алфавитalphabet = "abcdefghijklmnopqrtsuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ"list_symbols = [i for i in alphabet]#Количество разбиенийINTERVAL = len(list_symbols)#Сопоставляем символы с их вероятностями распределёнными по нормальному законуprob = probabilities(np.array(random_value(N)))#Словарь кодов по Хаффмануdict_contained_symbols_and_codes_huffman = huffman_encoding(dict(zip(list_symbols, prob)))dict_contained_symbols_and_codes_shannon_fano = {}#print(dict(zip(symbols, prob)))shannon_fano_encoding(dict(zip(list_symbols, prob)))print_dict(dict(zip(list_symbols, prob)), "probabilities.txt")print_dict(dict_contained_symbols_and_codes_huffman, "huffman.txt")print_dict(dict_contained_symbols_and_codes_shannon_fano, "shannon-fano.txt")print('Результаты кодировки символов, вероятности которых распределены по нормальному закону')print(f"Длина кодировки.Прямое кодировании: {ceil(log(len(list_symbols), 2))}")print(f"Средняя длина кодовой последовательности по Хаффману: {len(''.join(dict_contained_symbols_and_codes_huffman.values())) / len(list_symbols):.2f}")print(f"Средняя длина кодовой последовательности по Шеннону-Фано: {len(''.join(dict_contained_symbols_and_codes_shannon_fano.values())) / len(list_symbols):.2f}")st = ''while (st!='exit'):st = input("Введите строку, которую хотите закодировать: ")print(f"Длина исходной строки: {len(st) * 8} бит")encoded_string_huffman = ''.join(map(str, encode_string(st, dict_contained_symbols_and_codes_huffman)))encoded_string_shannon_fano = ''.join(map(str, encode_string(st, dict_contained_symbols_and_codes_shannon_fano)))print(f"Кодовая последовательность, полученная при кодировании по Хаффману: {encoded_string_huffman}")print(f"Длина строки: {len(encoded_string_huffman)} бит")print(f"Кодовая последовательность, полученная при кодировании по Шеннону-Фано: {encoded_string_shannon_fano}")print(f"Длина строки: {len(encoded_string_shannon_fano)} бит") Результат работы программы:Рассмотрим длины кодовых последовательностей символов алфавита, состоящего из цифр 0-9, распределённых по нормальному закону (рисунок 1):

---

Рисунок 1 – длины последовательностейРаспределение вероятностей представлена в таблице 1.Таблица 1 – распределение вероятностей

0	0.000276
1	0.005329
2	0.042434
3	0.158443
4	0.297179
5	0.294982
6	0.155158
7	0.041089
8	0.004891
9	0.000219

Кодовые последовательности, полученные методом кодирования Хаффмана в соответствии с нормальным законом распределения представлены в таблице 2.Таблица 2 – кодовые последовательности, полученные методом Хаффмана.

0	10101010
1	101011
2	1011
3	11
4	00
5	01
6	100
7	10100
8	1010100
9	10101011

Кодовые последовательности, полученные методом кодирования Шеннона - Фано в соответствии с нормальным законом распределения представлены в таблице 3.Таблица 3 - Кодовые последовательности, полученные методом Шеннона - Фано

0	11110
1	11100
2	1100
3	100
4	00
5	01
6	101
7	1101
8	11101
9	11111

---

Метод Хаффмана эффективен при кодировке символов с высокой вероятностью, т.к. для них средняя длина кодировки значительно меньше средней длины маловероятных символов. Метод Шеннона-Фано напротив эффективней метода Хаффмана в кодировке символов с низкой вероятностью, т.к. средняя длина кодировки распределяется для них более линейно.Закодируем последовательность ‘3455543435553’ (рисунок 2).Рисунок 2 – кодирование последовательности ‘3455543435553’Заметим, что длина кодовой последовательности по Хаффману короче, чем по Шеннону-Фано, что подтверждает вышесказанное, метод Хаффмана эффективен при кодировании высоковероятных символов.Закодируем последовательность ‘39012930121009’ (рисунок 3).Рисунок 3 – кодирование последовательности ‘39012930121009’Заметим, что длина кодовой последовательности по Шеннону-Фано значительно короче кодовой последовательности по Хаффману, что подтверждает вышесказанное, метод Шеннона-Фано значительно эффективнее при кодировании символов с низкой вероятностью.Рассмотрим принцип, по которому цифры 1-9 были закодированы методом Шеннона-Фано, используя вероятности из таблицы 1. 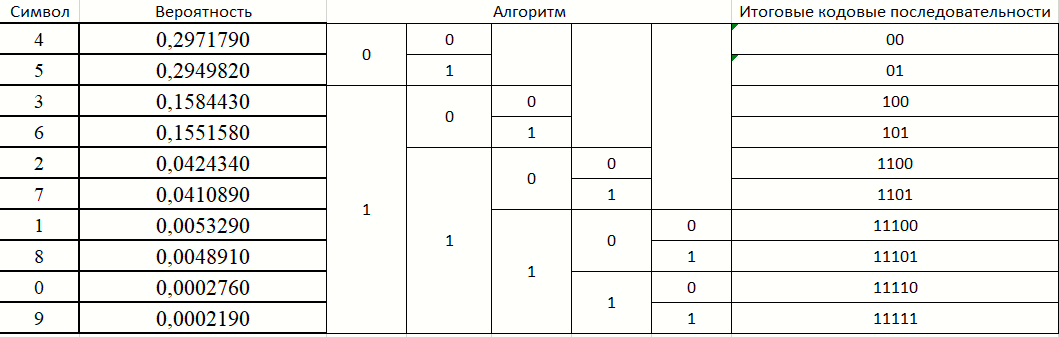(рисунок 3)Рисунок 4 – Кодирование алфавита методом Шеннона-ФаноРассмотрим принцип, по которому цифры 1-9 были закодированы методом Хаффмана, используя вероятности из таблицы 1. 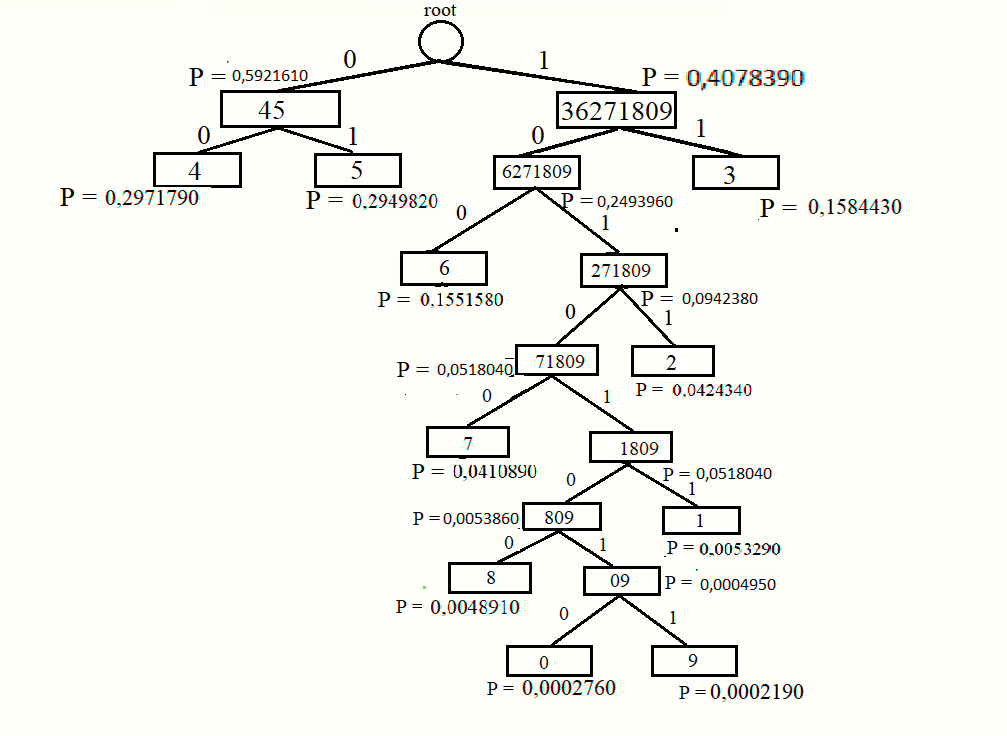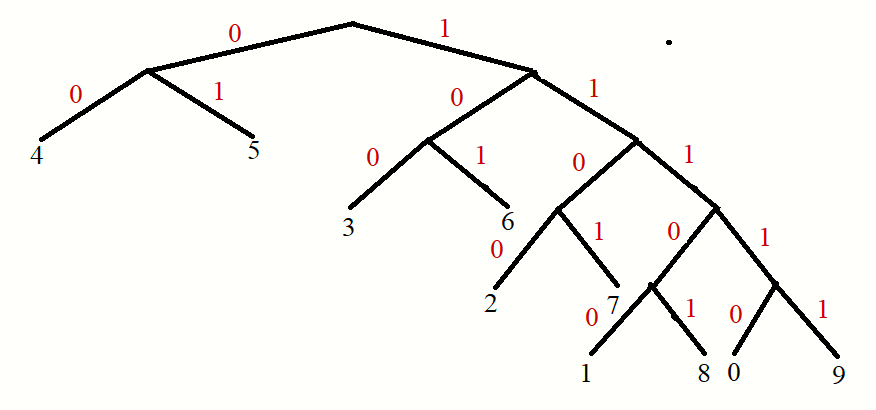(рисунок 4)Рисунок 5 – Кодирование алфавита методом ХаффманаРассмотрим принцип кодирования методом Шеннона-Фано в виде бинарного дерева (рисунок 5):Рисунок 5 – Бинарное дерево по Шеннону-ФаноРассмотрим кодирование символов алфавита (рисунок 6).

---

Рисунок 6 – длины последовательностейПолученные вероятности, распределённые по нормальному закону представлены в таблице 4.Таблица 4 – распределение вероятностей

W 0.02213 X 0.02323 Y 0.024127 Z 0.025078 а 0.025909 б 0.026715 в 0.026982 г 0.028007 д 0.028076 е 0.028461 ё 0.028526 ж 0.02846 з 0.028508 и 0.028178

й 0.027743 к 0.026839 л 0.026364 м 0.025398 н 0.024386 о 0.023522 п 0.02245 р 0.021173 с 0.02014 т 0.018789 у 0.017556 ф 0.016565 х 0.015163 ц 0.014001

ч 0.012668 ш 0.011554 щ 0.010394 ъ 0.009399 ы 0.008411 ь 0.00746 э 0.006688 ю 0.005661 я 0.005116 А 0.00439 Б 0.003909 В 0.003335 Г 0.002818 Д 0.002273

Е 0.002018 Ё 0.001691 Ж 0.001314 З 0.001176 И 0.000922 Й 0.000747 К 0.000617 Л 0.000501 М 0.000397 Н 0.000305 О 0.000252 П 0.000176 Р 0.000146 С 9.8e-05

Т 0.000103 У 6.6e-05 Ф 3.2e-05 Х 3.8e-05 Ц 2.4e-05 Ч 2.1e-05 Ш 1.2e-05 Щ 9e-06 Ъ 3e-06 Ы 2e-06 Ь 6e-06 Э 4e-06 Ю 1e-06 Я 0.0

Кодовые последовательности, полученные методами Шеннона-Фано и Хаффмана представлены в таблице 5.Таблица 5

Хаффман			Шеннон - Фано
Ё 0000000000 z 0000000001 D 000000001 t 000000010000 С 00000001000100 j 0000000100010100 f 00000001000101010 Ь 000000010001010110 a 0000000100010101110 Ы 0000000100010101111 k 000000010001011 p 0000000100011 v 00000001001 Й 00000001010 П 0000000101100 m 00000001011010 Ч 0000000101101100 h 00000001011011010 Щ 00000001011011011 Х 000000010110111 Н 000000010111 Г 000000011 ш 0000001 о 000001 X 000010 N 0000110 ю 00001110 H 00001111 п 000100 W 000101 р 000110 V 000111 щ 0010000 C 001000100 Ж 0010001010 y 0010001011 я 00100011 с 001001 U 001010 M 0010110 G 00101110 К 00101111000 u 00101111001 З 0010111101 B 001011111 т 001100 T 001101 ъ 0011100 L 0011101 у 001111 S 010000 Д 010001000 x 0100010010 r 010001001100 Р 0100010011010 e 01000100110110000 g 01000100110110001 i 0100010011011001 Ф 010001001101101	У 01000100110111 Л 01000100111 А 01000101 ы 0100011 ф 010010 K 0100110 F 01001110 Е 010011110 A 010011111 R 010100 х 010101 Б 01011000 E 01011001 ь 0101101 Q 010111 ё 01100 з 01101 е 01110 ж 01111 и 10000 д 10001 J 1001000 О 100100100000 q 100100100001 s 10010010001 И 1001001001 w 1001001010 o 1001001011000 l 10010010110010 Э 100100101100110000 c 1001001011001100010 Ю 10010010110011000110 Я 100100101100110001110 b 100100101100110001111 Ъ 100100101100110010 d 100100101100110011 Ш 1001001011001101 Ц 100100101100111 Т 1001001011010 n 1001001011011 М 10010010111 В 10010011 ц 100101 г 10011 й 10100 в 10101 к 10110 б 10111 P 110000 э 1100010 I 1100011 л 11001 а 11010 м 11011 ч 111000 O 111001 Z 11101 н 11110 Y 11111	ё 000000 з 000001 е 00001 ж 00010 и 00011 д 00100 г 00101 й 00110 в 00111 к 010000 б 010001 л 01001 а 01010 м 01011 Z 011000 н 011001 Y 01101 о 01110 X 01111 п 100000 W 100001 р 100010 V 100011 с 100100 U 100101 т 10011 T 101000 у 101001 S 101010 ф 101011 R 101100 х 101101 Q 10111 ц 1100000 P 1100001 ч 110001 O 110010 ш 110011 N 1101000 щ 1101001 M 110101 ъ 1101100 L 1101101 ы 110111 K 1110000 ь 1110001 J 1110010 э 1110011 I 11101000 ю 11101001 H 1110101 я 1110110 G 1110111 А 11110000 F 11110001 Б 11110010 E 11110011 В 11110100 D 11110101		Г 11110110 C 11110111 B 111110000 Д 111110001 Е 11111001 A 111110100 Ё 111110101 z 111110110 Ж 111110111 y 1111110000 З 1111110001 x 111111001 И 1111110100 w 1111110101 v 1111110110 Й 1111110111 К 11111110000 u 11111110001 Л 1111111001 s 11111110100 М 11111110101 t 1111111011 Н 111111110000 r 111111110001 О 11111111001 q 11111111010 p 11111111011 П 1111111110000 Р 1111111110001 o 111111111001 Т 111111111010 n 111111111011 С 1111111111000 m 1111111111001 У 1111111111010 l 1111111111011 k 11111111111000 Х 11111111111001 Ф 111111111110100 j 111111111110101 Ц 11111111111011 Ч 111111111111000 i 111111111111001 f 111111111111010 Ш 111111111111011 h 1111111111111000 e 1111111111111001 Щ 1111111111111010 g 1111111111111011 Ь 11111111111111000 Э 11111111111111001 a 1111111111111101 d 11111111111111100 Ъ 11111111111111101 c 111111111111111100 Ы 111111111111111101 Ю 111111111111111110 b 1111111111111111110 Я 1111111111111111111

---

Смотрите также файлы

• Введение в курс пожарностроевая и тактикоспециальная подготовка.docx

• Конституционное регулирование создания политических партий.doc

• ВключениеВыключение Насоса.doc

• Современные дети и гаджеты вред и польза.docx

• Порошки.docx