Добавлен: 09.01.2024
Просмотров: 44
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Математическая модель непериодического колебания имеет вид:
Для радиотехники интерес представляют импульсные (одиночные) сигналы. Преобразование Фурье является инструментом спектрального анализа непериодических (импульсных) сигналов (их еще называют сигналами конечной длительности, или финитными, т. е. пространственно ограниченными).
Положим, что некоторая функция U(t) аналитически описывает одиночный импульсный сигнал конечной длительности. Мысленно дополнив его такими же импульсными сигналами. Для того чтобы вне искусственно введенного интервала времени 0 ... Т исходный сигнал был равен нулю, необходимо увеличить период повторения этих импульсов. В пределе, при увеличении длительности периода и Т
, все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность импульсов Uk(t) вновь станет одиночным импульсом U(t). В этом случае выражения (7) и (8) сохраняют смысл. Подставив соотношение (8) в формулу (7), запишем периодическую функцию:
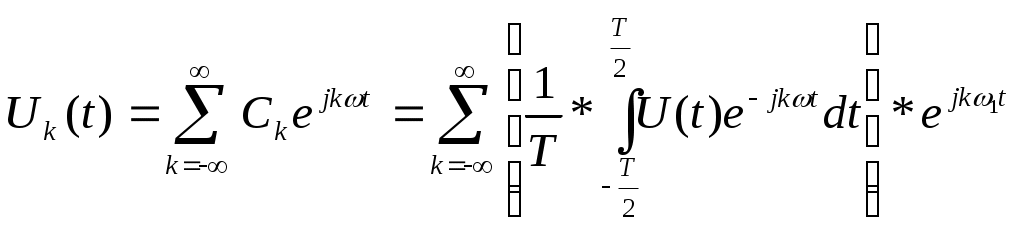(11)Так как период следования импульсов Т= 2π/
1 то:
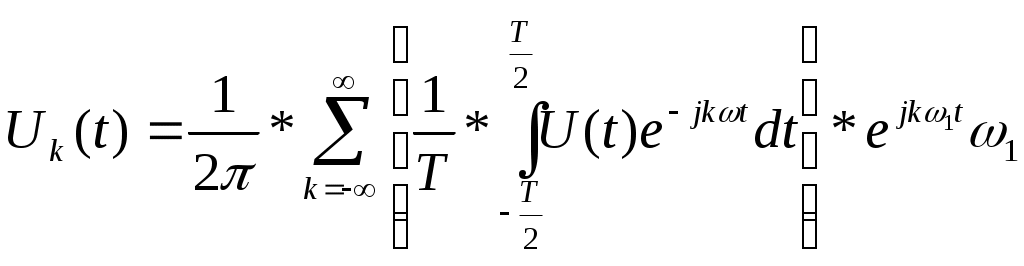(12)В предельном случае, когда Т
, равные расстояния между спектральными линиями уменьшатся настолько, что спектр станет сплошным, а амплитуды отдельных спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов 1 = 2
/Т 
0 и превращается в d , дискретная переменная k 1 - в мгновенную (текущую) частоту
, а сумма трансформируется в интеграл. Периодическая последовательность импульсов Uk(t) станет одиночным импульсом U(t), и выражение (12) запишется в виде:
Интеграл в скобках есть комплексная функция частоты. Обозначив его:
(13)Получим:
(14)Соотношения (13) и (14) носят фундаментальный характер в теории сигналов и определяют соответственно прямое и обратное преобразования Фурье. Они связывают между собой вещественную функцию времени U(t) и комплексную функцию частоты S(
). Если использовать не угловую частоту со, а циклическу f =
/(2π), то формулы прямого (13) и обратного (14) преобразования Фурье становятся еще более симметричными, отличаясь лишь знаком в показателе:
(15)
(16)
прямоугольный импульс временная диграмма
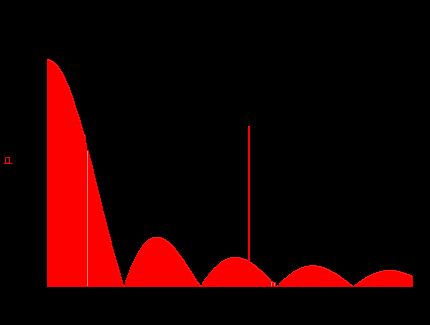
модуль спектральной плотности
Список литературы:
Сергиенко А. Б. Цифровая обработка сигналов: учебное пособие.- 3-изд. – СПб.: БХВ - Петербург, 2011. – 768 с.
Якимов Е. В. Цифровая обработка сигналов: учебное пособие/ Е. В. Якимов, Г. В. Вавилова, И. А. Клубович. – Томск: изд-во Томского политехнического университета, 2008. – 307 с.