Файл: Контрольная работа задание 2 5 вариант ст гр. Гпуд 171бз Мартюченко В. О. Проверил доцент Косякин С. И.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, соответствующий переменной x3, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (5.94 : 0.24, 6.77 : -0.16 , 6.54 : 6.79 , 8.88: 0.58 , 2.93 : 5.35, 0.13:5.27 ) = 0.02
Следовательно, 6-ая строка является ведущей.
Разрешающий элемент равен (5.27) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x10 в план 3 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 3, получена в результате деления всех элементов строки x10 плана 2 на разрешающий элемент РЭ=5.27. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули.
Таким образом, в новом плане 3 заполнены строка x3 и столбец x3. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так:
x1 = 8.84, x2 = 0, x3 = 0.019, x4 = 5.94
F(X) = 0.33*8.84 + 0.27*0 + 0.3*0.019 + 0.25*5.94 = 4.408
Ответ:
1. Найти оптимальный план производства краски каждого вида, который обеспечивает получение максимального дохода
1. F(X) = 0.33*8.84 + 0.27*0 + 0.3*0.019 + 0.25*5.94 = 4.408
2. Определить пределы изменения дефицитных запасов сырья
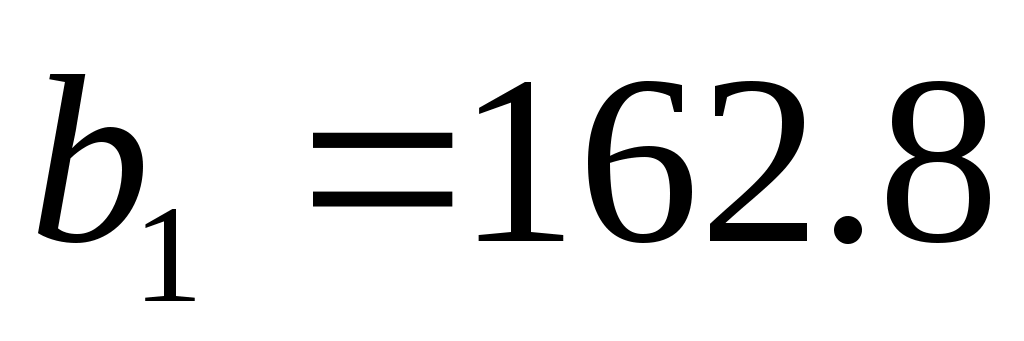
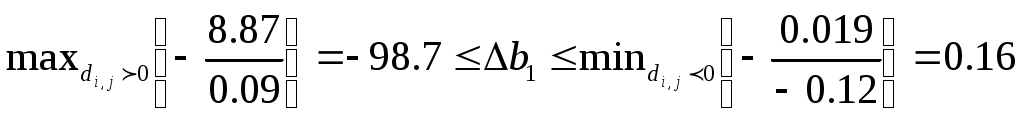
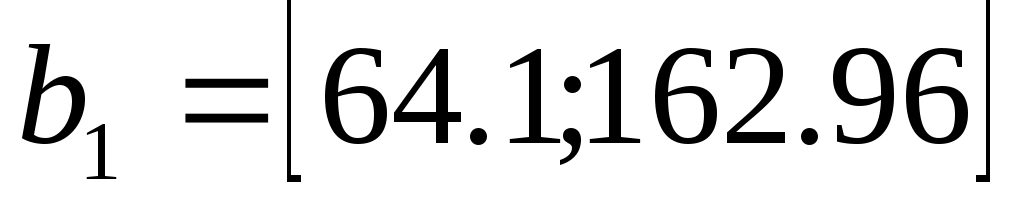
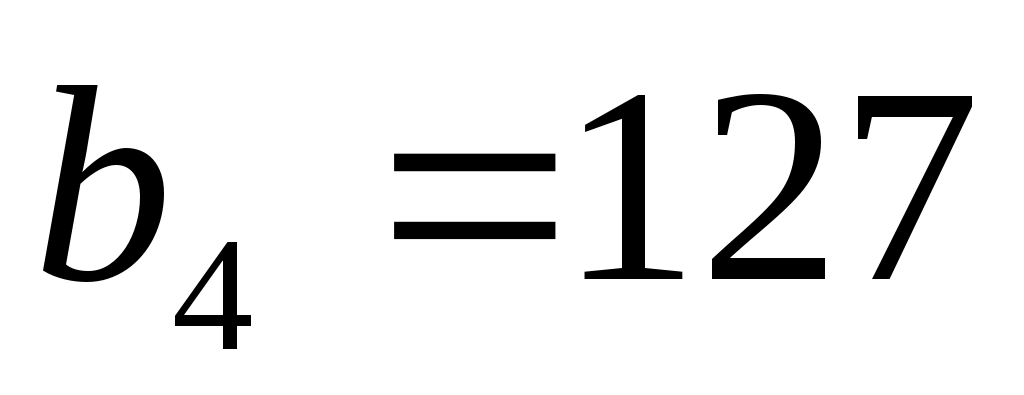
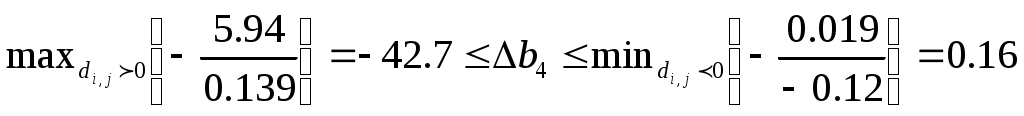
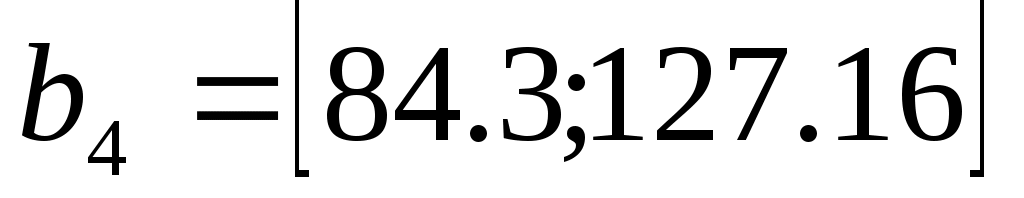
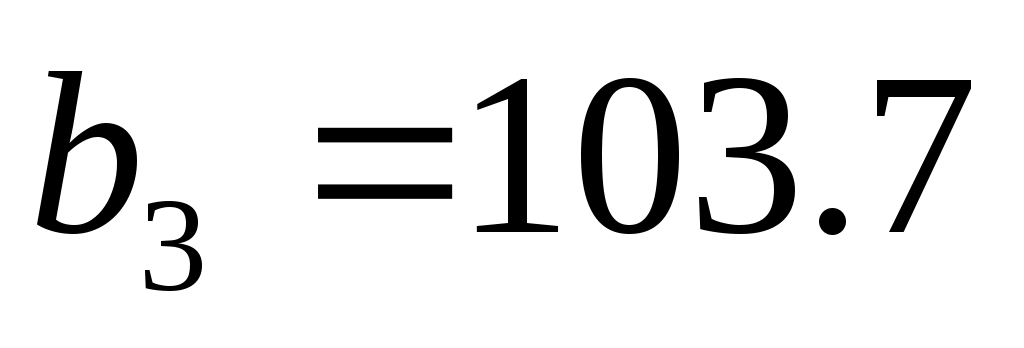
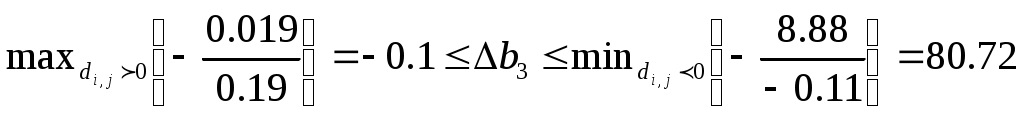
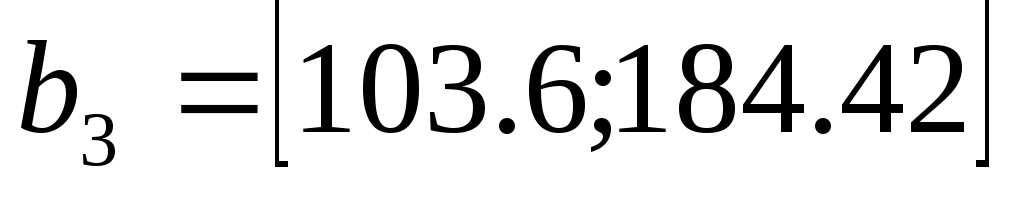
3. Определить неявную стоимость дефицитных видов сырья
Значение 0 в столбце x6 означает, что неявная стоимость 2 вида сырья равна 0.
Значение 0 в столбце x7 означает, что неявная стоимость 3 вида сырья равна 0.
Значение 0 в столбце x9 означает, что неявная стоимость 4 вида сырья равна 0.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (5.94 : 0.24, 6.77 : -0.16 , 6.54 : 6.79 , 8.88: 0.58 , 2.93 : 5.35, 0.13:5.27 ) = 0.02
Следовательно, 6-ая строка является ведущей.
Разрешающий элемент равен (5.27) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | min |
| x4 | 5.95 | 0 | -0.611 | 0.24 | 1 | 0.11 | 0 | 0 | -0.09 | 0 | 0 | 24.75 |
| x6 | 6.77 | 0 | 10.58 | -0.16 | 0 | -1.28 | 1 | 0 | 0.54 | 0 | 0 | - |
| x7 | 6.54 | 0 | 3.76 | 6.79 | 0 | -0.85 | 0 | 1 | 0.18 | 0 | 0 | 0.93 |
| x1 | 8.88 | 1 | 1.24 | 0.58 | 0 | -0.02 | 0 | 0 | 0.09 | 0 | 0 | 15.31 |
| x9 | 2.93 | 0 | -6.15 | 5.35 | 0 | -0.12 | 0 | 0 | -0.81 | 1 | 0 | 0.55 |
| x10 | 0.1 | 0 | 10.54 | 5.27 | 0 | -0.63 | 0 | 0 | 0 | 0 | 1 | 0.02 |
| F(X3) | 4.41 | 0 | -0.012 | -0.049 | 0 | 0.021 | 0 | 0 | 0.0067 | 0 | 0 | |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x10 в план 3 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 3, получена в результате деления всех элементов строки x10 плана 2 на разрешающий элемент РЭ=5.27. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули.
Таким образом, в новом плане 3 заполнены строка x3 и столбец x3. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:
| B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |
| 5.95-(0.13*0.24):5.27 | 0-(0*0.24):5.27 | -0.611-(10.54*0.24):5.27 | 0.24-(5.27*0.24):5.27 | 1-(0*0.24):5.27 | 0.11-(-0.63*0.24):5.27 | 0-(0*0.24):5.27 | 0-(0*0.24):5.27 | -0.09-(0*0.24):5.27 | 0-(0*0.24):5.27 | 0-(1*0.24):5.27 |
| 6.77-(0.13*-0.16):5.27 | 0-(0*-0.16):5.27 | 10.58-(10.54*-0.16):5.27 | -0.16-(5.27*-0.16):5.27 | 0-(0*-0.16):5.27 | -1.28-(-0.63*-0.16):5.27 | 1-(0*-0.16):5.27 | 0-(0*-0.16):5.27 | 0.54-(0*-0.16):5.27 | 0-(0*-0.16):5.27 | 0-(1*-0.16):5.27 |
| 6.54-(0.13*6.79):5.27 | 0-(0*6.79):5.27 | 3.76-(10.54*6.79):5.27 | 6.79-(5.27*6.79):5.27 | 0-(0*6.79):5.27 | -0.85-(-0.63*6.79):5.27 | 0-(0*6.79):5.27 | 1-(0*6.79):5.27 | 0.18-(0*6.79):5.27 | 0-(0*6.79):5.27 | 0-(1*6.79):5.27 |
| 8.88-(0.13*0.58):5.27 | 1-(0*0.58):5.27 | 1.24-(10.54*0.58):5.27 | 0.58-(5.27*0.58):5.27 | 0-(0*0.58):5.27 | -0.02-(-0.63*0.58):5.27 | 0-(0*0.58):5.27 | 0-(0*0.58):5.27 | 0.09-(0*0.58):5.27 | 0-(0*0.58):5.27 | 0-(1*0.58):5.27 |
| 2.93-(0.13*5.35):5.27 | 0-(0*5.35):5.27 | -6.15-(10.54*5.35):5.27 | 5.35-(5.27*5.35):5.27 | 0-(0*5.35):5.27 | -0.12-(-0.63*5.35):5.27 | 0-(0*5.35):5.27 | 0-(0*5.35):5.27 | -0.81-(0*5.35):5.27 | 1-(0*5.35):5.27 | 0-(1*5.35):5.27 |
| 0.1:5.27 | 0 : 5.27 | 10.54 : 5.27 | 5.27 : 5.27 | 0 : 5.27 | -0.63 : 5.27 | 0 : 5.27 | 0 : 5.27 | 0 : 5.27 | 0 : 5.27 | 1 : 5.27 |
| 4.41 | 0-(0*0):5.27 | -0.012-(10.54*-0.049):5.27 | -0.049-(5.27*-0.049):5.27 | 0-(0*-0.049):5.27 | 0.021-(-0.63*-0.049):5.27 | 0-(0*-0.049):5.27 | 0-(0*-0.049):5.27 | 0.0067-(0*-0.049):5.27 | 0-(0*-0.049):5.27 | 0-(1*-0.049):5.27 |
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |
| x4 | 5.94 | 0 | -1.09 | 0 | 1 | 0.139 | 0 | 0 | -0.09 | 0 | -0.046 |
| x6 | 6.77 | 0 | 10.9 | 0 | 0 | -1.26 | 1 | 0 | 0.54 | 0 | 0.03 |
| x7 | 6.37 | 0 | -9.82 | 0 | 0 | -0.04 | 0 | 1 | 0.18 | 0 | -1.29 |
| x1 | 8.87 | 1 | 0.08 | 0 | 0 | 0.05 | 0 | 0 | 0.09 | 0 | -0.11 |
| x9 | 2.8 | 0 | -16.85 | 0 | 0 | 0.52 | 0 | 0 | -0.81 | 1 | -1.015 |
| x3 | 0.13 | 0 | 2 | 1 | 0 | -0.12 | 0 | 0 | 0 | 0 | 0.19 |
| F(X3) | 4.41 | 0 | 0.086 | 0 | 0 | 0.015 | 0 | 0 | 0.0067 | 0 | 0.0093 |
1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |
| x4 | 5.94 | 0 | -1.09 | 0 | 1 | 0.139 | 0 | 0 | -0.09 | 0 | -0.046 |
| x6 | 6.77 | 0 | 10.9 | 0 | 0 | -1.26 | 1 | 0 | 0.54 | 0 | 0.03 |
| x7 | 6.37 | 0 | -9.82 | 0 | 0 | -0.04 | 0 | 1 | 0.18 | 0 | -1.29 |
| x1 | 8.87 | 1 | 0.08 | 0 | 0 | 0.05 | 0 | 0 | 0.09 | 0 | -0.11 |
| x9 | 2.8 | 0 | -16.85 | 0 | 0 | 0.52 | 0 | 0 | -0.81 | 1 | -1.015 |
| x3 | 0.019 | 0 | 2 | 1 | 0 | -0.12 | 0 | 0 | 0 | 0 | 0.19 |
| F(X4) | 4.41 | 0 | 0.086 | 0 | 0 | 0.015 | 0 | 0 | 0.0067 | 0 | 0.0093 |
Оптимальный план можно записать так:
x1 = 8.84, x2 = 0, x3 = 0.019, x4 = 5.94
F(X) = 0.33*8.84 + 0.27*0 + 0.3*0.019 + 0.25*5.94 = 4.408
Ответ:
1. Найти оптимальный план производства краски каждого вида, который обеспечивает получение максимального дохода
1. F(X) = 0.33*8.84 + 0.27*0 + 0.3*0.019 + 0.25*5.94 = 4.408
2. Определить пределы изменения дефицитных запасов сырья
3. Определить неявную стоимость дефицитных видов сырья
Значение 0 в столбце x6 означает, что неявная стоимость 2 вида сырья равна 0.
Значение 0 в столбце x7 означает, что неявная стоимость 3 вида сырья равна 0.
Значение 0 в столбце x9 означает, что неявная стоимость 4 вида сырья равна 0.