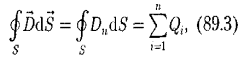(11)

т.е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума Dn = ε₀Е_п (ε=1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность равен

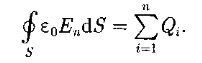(12)

Так как источниками поля Ё в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Ё в самом общем виде можно записать как

(13)

Где соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Ё в диэлектрике, так как она выражает свойства неизвестного поля Ё через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения. [1]
Глава 4. Граничные условия

Рассмотрим связь между векторами Ё и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых ε₁и ε₂) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис. 2. Согласно теореме о циркуляции вектора Е,

---

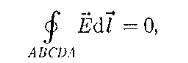
откуда



(знаки интегралов по АВ и СDразные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DAничтожно малы). Поэтому

Eτ1=Eτ2

(14)

Рисунок 2. Замкнутый прямоугольный контур АBCDA

Заменив, согласно (8), проекции вектора Ё проекциями вектора D, деленными на ε₀ε, получим

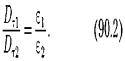(15)

На границе раздела двух диэлектриков (рис. 3) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор Dодинаков. Согласно теореме Гаусса (11), D_µ1ΔS- D_µ2ΔS=0

(нормали п и п' к основаниям цилиндра направлены противоположно). Поэтому

Dµ1= Dµ2	(16)
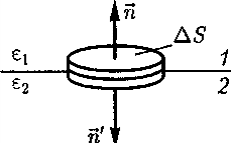Рисунок 3. Прямой цилиндр

Заменив, согласно (8), проекции вектора D проекциями вектора Е, умноженными на ε₀ε, получим

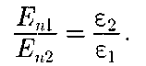(17)

Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора (Еτ)и нормальная составляющая вектора D(D_n)изменяются непрерывно (не претерпевают скачка), а нормальная состав-ляющая вектора (Е_n) и тангенциальная составляющая вектора D(Dτ)претерпевают скачок. [1]

---

Из условий (14)—(17) для составляющих векторов 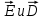следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами α₁ и α₂ (на рис. 4 ε₂>ε1). Согласно (14) и (17), E_τ1=E_τ2 и ε₂E_n2= ε₁E_n1

Разложим векторы Е₁ и Е₂у границы раздела на тангенциальные и нормальные составляющие. Из рис. 4 следует

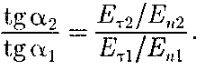
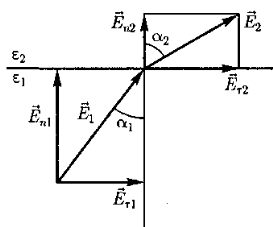Рисунок 4. Связь между углами α1 и α2

Учитывая записанные выше условия, получим закон преломления линий напряженности Е (а значит, и линий смещения D)



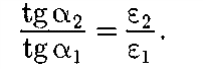
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали. [1]
Заключение

Электрическое поле — особая форма поля, существующая вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде в электромагнитных волнах. Электрическое поле непосредственно невидимо, но может наблюдаться по его действию и с помощью приборов. Основным действием электрического поля является ускорение тел или частиц, обладающих электрическим зарядом.

Электрическое поле можно рассматривать как математическую модель, описывающую значение величины напряженности электрического поля в данной точке пространства.

Электрическое поле является одной из составляющих единого электромагнитного поля и проявлением электромагнитного взаимодействия.
Список литературы

1. 
   Курс физики: учеб. пособие для вузов / Таисия Ивановна Трофимова. — 11-е изд., стер. — М.: Издательский центр «Академия», 2006. — 560 с. (дата обращения 01.03.2022 г.)
   

---

Смотрите также файлы

• Анализ показателей федерального бюджета рф.docx

• Личностно ориентированное обучение.doc

• Практическое задание 1 Основные управленческие характеристики менеджера.docx

• Закон Ома для участка цепи ток в проводнике i равен отношению падения напряжения u на участке цепи к ее электрическому сопротивлению r i u r. (1) Закон Ома для полной цепи.docx

• Кол во.docx