ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 92
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В прошлом веке в итоге исследований в отрасли математики К. Геделя, А. Чёрча, А. Тьюринга, А. А. Маркова, А. М. Колмогорова определился широкий круг процессов, которым присущи следующие свойства:
1) в принципе строго детерминированы, т. е. каждый предыдущий этап полностью определяет следующие;
2) потенциально осуществимы – с той точки зрения, что при длительном протекании без внешних препятствий приводят к фактическому результату;
3) имеют атомарное строение – состоят из совокупности элементарных операций, которых имеется лишь несколько видов;
4) заключаются в преобразовании объектов, которые четко различимы, и поэтому удобны для человеческого восприятия, запоминания и мышления [3].
Для описания и исследования такого рода процессов, которые получили название алгоритмических, возникла теория алгоритмов, как раздел математики.
В этой теории основное ударение делается на понятии принципиальной вычислимости алгоритмов, а форма представления алгоритма особой роли не играет. При этом характерной особенностью алгоритма является выбор минимальных средств для представления и преобразования информации, что диктуется с точки зрения удобства формализации самого понятия алгоритма. Но процедуры конкретных вычислений, записанные с помощью такого рода алгоритмических систем, как правило, настолько громоздкие и сложные для понимания, что в реальной практике не могут быть использованными. Это касается прикладной математики и особенно информатики [21].
Поэтому для практической реализации алгоритмических методов преобразования информации на базе классической теории алгоритмов возникает прикладная теория алгоритмов. При этом применение алгоритмических методов исследования выходит за пределы математики, кибернетики, информатики. Это произошло потому, что «представление посредством алгоритмов позволяет выявить определенные закономерности в поведении сложной системы, взаимосвязь частей, что ее составляют, изучить ее динамические характеристики.
Место формул, не отрицая их, а обобщая, заняли алгоритмы» [1; 14]. То есть речь уже идет не об отдельном изолированном разделе математики или информатики, а об отдельной методологии научного исследования. Понятие алгоритма проникло в отрасли гуманитарных и общественных дисциплин, например, в психологию – для описания психических процессов, в педагогику – для описания и организации процесса обучение и т. др. Но в связи с использованием в «размытых», не сформированных формально областях науки, произошло и определенное «размытие» самого термина «алгоритм». И это понятно – ведь не все реальные процессы строго формальные.
Мир не исчерпывается лишь алгоритмическими формами. Даже в процессах, которые удается так или иначе описать посредством алгоритмов, есть неформализированные компоненты, недопустимые в пределах строгого математического понятия алгоритма. Поэтому применяются так называемые ослабления понятия алгоритма. В самой математике уже встречается понятие ослабления алгоритма (это ослабление реализуется в алгоритме сводимости – предписанию, которое сводит решение задач определенного типа к задачам, которые принимаются за уже решенные) [3].
В отличие от «абсолютных» алгоритмов, операции которых строго формальные, определенные предписания алгоритмического типа допускают правила, которые имеют смысловой характер. Например, если в качестве исполнителя выступает человек, то алгоритмы могут содержать действия, что существенно зависят от человеческого понимания; в силу этого операции, из которых состоят предписания, могут быть, по сути дела, достаточно сложными «блоками» умственных действий – лишь бы исполнитель, например, человек, мог оперировать без осложнений такими «смысловыми блоками».
Таким образом, на данный момент можно выделить три смысловых значения, которые могут интерпретировать понятие алгоритма:
1) как строго определенный математический объект;
2) как термин, используемый в прикладной теории алгоритмов – эмпирическое понятие, но сам алгоритм является строгим формальным предписанием;
3) как термин, используемый в ослабленном, «размытом» значении [25].
С точки зрения обучения алгоритмике в школе наиболее пригодно понятие алгоритма, используемое в прикладной теории алгоритмов. Эмпирическое понятие алгоритма, с одной стороны, является формальным, что отличает его от «размытого», а, с другой стороны, является понятным, простым для применения в сравнении с его математическим толкованием.
Существует множество толкований алгоритма. Например:
1) алгоритм – точное предписание, которое определяет вычислительный процесс, что ведет от варьируемых исходных данных к искомому результату [13];
2) алгоритм – способ (программа) решения вычислительных и других задач, которая точно приписывает, как и в какой последовательности получить результат, который однозначно определяется входными данными [18];
3) алгоритм – система операций (например, вычислений), что применяются по строго определенным правилам, которая после последовательного их выполнения приводит к решению поставленной задачи [15].
Алгоритм может приобретать две формы – идеальную и знаковую (рис. 1). Идеальная форма является отображением ментального образа алгоритма в ментальном пространстве человека, носителем семантического значения алгоритма. Знаковая форма есть своеобразной промежуточной формой, и служит для передачи алгоритма от конструктора алгоритма к его исполнителю, а также для сохранения алгоритма для последующего использования [6].
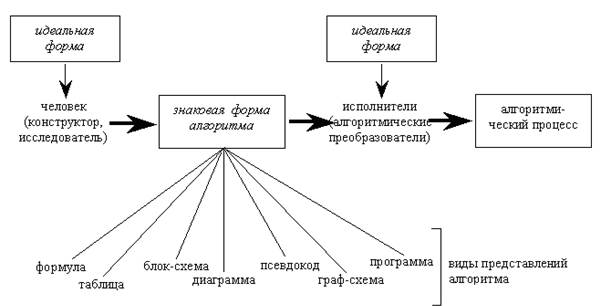
Рис. 1.1. Формы алгоритма
Следовательно, знаковая форма необходима, во-первых, для устранения семантической разницы в интерпретации алгоритма конструктором и исполнителем а, во-вторых, для сохранения или передачи алгоритма для последующего применения.
Понятно, что прежде чем научиться конструировать, составлять алгоритмы, и через них порождать алгоритмические процессы и руководить ими, нужно понять закономерности, которые имеют место в самих этих процессах. Но в большинстве случаев алгоритмический процесс наблюдать невозможно в результате его непосредственной недоступности для человека [19].
Таким образом, знаковая форма является самостоятельным объектом, который реально существует и замещает другой реальный объект – алгоритмический процесс. При этом выполняется условие: алгоритм не совпадает полностью с соответствующим ему алгоритмическим процессом, но исследование алгоритма дает полную информацию о протекании процесса.
Поэтому знаковую форму алгоритма можно назвать моделью алгоритмического процесса. Заметим, что если принять такую точку зрения, то, по отношению к описанию информационной модели, алгоритм выступает в качества метамодели. Признание знаковой формы алгоритма как определенной модели позволяет распространить на нее общие методы работы с моделями, т.е. алгоритмизация является моделированием алгоритмических процессов.
Знаковая форма алгоритма в качестве модели выступает и как продукт, и как средство осуществления теоретической деятельности через наглядно-образные формы. Это позволяет утверждать, что алгоритмы-модели являются своеобразным сочетанием чувственного и рационального в познании. Этот вывод важен, потому что позволяет по-новому взглянуть на дидактическое значение и применение представлений алгоритмов [14].
При правильном выборе алгоритмического представления можно развивать не только теоретическое мышление, но и наглядно-образное. Например, можно с достаточной достоверностью прогнозировать, что применение графическо-символьных представлений алгоритмов будет способствовать обучению алгоритмике детей, в которых преобладает наглядно-образный компонент над аналитическим.
Также особенно нужно отметить, что алгоритмы, как своеобразная форма наглядного представления процессов, используются не просто как иллюстрация некоторого положения, но и как отображение активных моделей.
Алгоритмы являются не просто иллюстративными моделями, которые односторонне воспроизводят алгоритмические процессы. Они являются также моделями проектирующими, то есть такими, что порождают эти процессы, позволяют их организовывать и реорганизовывать, полностью предугадывая их поведение [13].
Таким образом, алгоритмизация рассматривается нами как специфическая познавательно-проектирующая деятельность. Алгоритмизация – это не просто знание алгоритмов и их воссоздание. Это, прежде всего, овладение общими способами действий, приемами, средствами создания и применения алгоритмов.
2. Разработка дидактического материала, направленного на
развитие алгоритмических способностей
2.1. Разработка конспекта урока по информатике и ИКТ по теме: «Алгоритм. Свойства алгоритма»
Конспект урока по информатике и ИКТ разработан для учащихся 6 класса, обучающихся по учебнику Л. Босовой.
Цель: ознакомление обучающихся с понятием алгоритма, его свойств, исполнителя алгоритма и основными алгоритмическими структурами.
Задачи:
1) обеспечить усвоение понятий алгоритм, исполнитель, свойства алгоритма, дать представление об основных алгоритмических структурах умения составлять простейшие блок-схемы алгоритмов;
2) способствовать развитию алгоритмического мышления, внимательности, информационной культуры;
3) формировать способность к самостоятельной работе, самоконтролю и правильной организации рабочего времени, содействовать профориентации учеников.
Ход занятия:
1.Организационный момент. Приветствие и объявление темы урока.
Добрый день, ребята! Сегодня, мы начнём изучать самую интересную и важную тему курса информатики «Алгоритм».
2.Этап подготовки обучающихся к активному сознательному усвоению знаний.
Учитель предлагает учащимся ответить на следующие вопросы:
1. Что такое алгоритм?
2. Для чего нужны алгоритмы?
3. Какими свойствами обладают алгоритмы?
4. Кто такой исполнитель?
Возникающие вопросы фиксируются на доске.
Каждый из нас ежедневно использует различные алгоритмы: инструкции, правила, рецепты и т.д. Обычно мы это делаем не задумываясь. Например, вы хорошо знаете, как заварить чай. Но допустим, нам надо научить этому младшего брата или сестру. Значит, нам придется четко указать действия и порядок их выполнения. Что это будут за действия и какой их порядок? Учащиеся составляют правило заваривания чая:
1. Вскипятить воду.
2. Окатить заварочный чайник кипятком.
3. Засыпать заварку в чайник.
4. Залить кипятком.
5. Закрыть крышечкой.
6. Накрыть полотенцем.
Другими словами мы составили алгоритм. Теперь попробуем дать определение алгоритма. Как вы думаете, что называется алгоритмом?
Алгоритм – это конечная последовательность действий, направленных на получение из исходных данных результата, записанная с помощью точных и понятных исполнителю команд.
Мой помощник, ваш одноклассник, подготовил историческую справку о происхождении слова «алгоритм» (Приложение 1), для этого он использовал учебник, справочники, интернет-ресурсы.
3. Этап усвоения новых знаний.
Итак, алгоритм – это описание детерминированной последовательности действий, направленных на получение из исходных данных результата за конечное число дискретных шагов с помощью понятных исполнителю команд.
1. Какие алгоритмы Вы знаете, и кто или что является исполнителями алгоритмов?
2. Как Вы понимаете высказывание Норберта Винера: «Любая машина стоит лишь столько, сколько стоит человек, который на ней работает?» Обмен мнениями в группах.
Исполнитель – человек, группа людей, животное, техническое устройство, способные выполнять заданные команды. Любая задача может быть успешно решена только тогда, когда она чётко описана. Из приведённого списка задач выберите те, которые сформулированы чётко:
1. Сосчитайте число окон в своём доме.
2. Сосчитайте звёзды на небе.
3. Дайте подробное описание дороги от двери своего дома до школы (пешком, на автобусе или другом транспорте).
4. Иди туда, не знаю куда.
5. Принеси то, не знаю что.
Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм. Рассмотрим следующие примеры.
Алгоритм открывания двери: