Схема для расчета осадок по методу послойного элементарного суммирования

1.-Элементарный слой до деформации;

2..-то же, после деформации.

 

80. От какого горизонта отсчитывается эпюра природного давления?

Эпюра природного давления отсчитывается от отметки поверхности грунта-от природного рельефа.

 

81. Какими принимаются боковые давления при расчете осадки способом послойного суммирования? Можно ли считать, что боковое расширение грунта в этом способе полностью не учитывается?

При расчете осадки способом послойного суммирования боковые деления принимаются такими, какими они получаются при сжатии грунта в одометре, то есть



Хотя при расчете осадок боковое расширение грунта в этом способе и не учитывается

(принимается, что боковые деформации равны нулю), но косвенно они учитываются тем, что распределение напряжений получено из решения теории упругости для полупрост-ранства (или полуплоскости), в котором считалось, что среда имела возможность боковых перемещений. Таким образом, оно непосредственно не учитывается, а косвенно и частично учтено.

 

82. В формуле расчета осадки способом послойного суммирования имеется коэффициент β. От чего он зависит?

Коэффициент βопределяется из выражения:



и, следовательно, зависит только от коэффициента Пуассона грунта μ₀ (коэффициента относительной поперечной деформации). В СНиП 2.02.01-83 условно принято постоянное значение для β(считается, что β= 0,8).

83. В каких пределах ведется суммирование осадки при расчете методом послойного суммирования?

Всегда ли принимается при определении положения нижней границы сжимаемой толщи коэффициент 0,2?

В методе послойного суммирования осадки суммируются до той отметки, когда осевые дополнительные по отношению к природным напряжения не снизятся до 20 % от природных (бытовых) на этой же отметке. Эта отметка считается нижней границей сжимаемой толщи (B.C.), а осадками за счет сжатия нижерасположенной толщи пренебрегают. Однако, если ниже расположены слабые грунты с модулем деформации 

---

Е < 5 МПа, то нижнюю границу сжимаемой толщи следует опустить до той отметки, где дополнительные по отношению к природным давления составят 10 % от природных, а не 20 % как обычно.

84.   Получается ли линейная зависимость осадки от нагрузки в методе послойного суммирования?

Нет, не получается в связи с тем, что положение нижней границы сжимаемой толщи изменяется в зависимости от действующего сверху осадочного давления - чем больше осадочное давление, тем ниже при прочих равных условиях будет положение нижней границы сжимаемой толщи. Поэтому зависимость осадки от нагрузки не будет линейной.

85.От каких факторов зависит положение нижней границы сжимаемой толщи в методе послойного суммирования (будет ли она располагаться ниже или выше)?

Зависит от:

- плотности грунтов основания;

- наличия горизонта грунтовых вод;

- заглубления фундамента;

- нагрузки на фундамент;

- ширины фундамента;

- соотношения сторон подошвы фундамента в плане;

- наличия слоя слабого грунта в основании.

86. Каким образом влияют расположенные рядом фундаменты друг на друга? Как строится эпюра напряжений σ_z при наличии расположенного рядом фундамента? Как поступить, если подошвы соседних фундаментов расположены в разных уровнях?

При расположении фундаментов рядом наличие одного из них влияет на осадку соседнего фундамента. Это обстоятельство следует учитывать при расчете осадки (рис.). Поэтому кдополнительным давлениям σ_z, рассчитываемого фундамента следует добавить значения напряжений σ_z, возникающих в этом месте от соседнего фундамента, пользуясь способом угловых точек. Если отметки подошвы одного и другого фундаментов одинаковы, то эпюра дополнительных давлений будет иметь нулевую ординату вверху. Если соседний фундамент 2 имеет более высоко расположенную подошву, то эпюра получит в уровне подошвы рассчитываемого фундамента 1 конечное значение дополнительного от соседнего фундамента 2 давления Δσ_z.

 



 

---

 

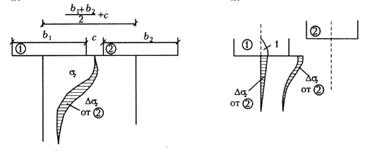
а) б)

Схемы для расчета осадок при наличии близко расположенных фундаментов:

а)- фундаменты 1 и 2 находятся рядом на одном уровне;

б)- фундамент 2 расположен выше, чем фундамент 1

87. Для какого случая получено решение задачи об осадке фундамента, в котором учитывается влияние всех компонентов напряжений?

Для однородного изотропного грунта, у которого и модуль деформации Е₀ и коэффициент Пуассона μ₀ постоянны.

88. Как вычислить значения модуля деформации грунта Ео_гнеобходимые для расчета осадки, по результатам штамповых испытаний в поле или компрессионных испытаний в одометре?

На кривой "осадка-нагрузка" штампа выбираются две точки, в пределах которых ведется спрямление. Рекомендуется, чтобы первая точка соответствовала бы давлению в грунте в точке отбора образца от собственного веса вышележащих слоев Р₁, а вторая соответствовала бы полному давлению Р₂от веса грунта иожидаемой нагрузки от сооружения. Имеется в виду, что кривая в диапазоне выбранных двух давлений хорошо бы аппроксимировалась прямой. Для вычисления модуля деформации Ео, МПа, используется формула

 



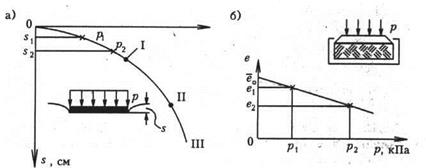 Здесь S₂ и S₁-см –величины осадки, соответствующие давлениям Р₁и Р₂,МПа; d –диаметр штампа, см; ω-коэффициент формы штампа, равный 0,85; μ₀- коэффициент Пуассона грунта, принимаемый обычно 0,3 для песков и супесей и 0,4 для глин. По результатам компрессионных испытаний в одометре величина Е₀,МПа, вычисляется по формуле:



Где е₁ и е₂- значения коэф. пористости, соответствующие давлениям р₁ и р₂

е₀ –начальный коэф. пористости.

 

а)штамповые испытания; б) компрессионные испытания

огда рекомендуется применять способ расчета осадки с использованием расчетной схемы в виде линейно-деформируемого слоя конечной толщины?

Этим способом предлагается пользоваться; еслимодуль деформации грунта основания более 100 МПа или если модуль деформации 

---

Е_о> 10 МПа; но ширина подошвы фундамента более 10 м. В этом случае осадочное давление считается равным полному.

90. Почему в формулу осадки для жесткого штампа на упругом полупространстве не входит глубина сжимаемой толщи?

Потому, что полупространство снизу не ограничено (толщина равна бесконечности) и при решении задачи отыскивается несобственный интеграл. Если бы толщина была ограничена конечным размером, она входила бы в окончательную формулу осадки.

91. От каких факторов зависит коэффициент ω в формуле осадки для полупространства? Чему он равен для круга, квадрата, "ленты"?

Этот коэффициент зависит от формы в плане загруженной площадки (квадрат, круг, прямоугольник), а также от жесткости штампа (гибкий штамп или жесткий). Для круга и жесткого штампа он равен 0,79, для квадрата - 0,88, для "ленты" (соотношение размеров сторон 10:1 и более) - 2,12.

 

92. С чем связано то обстоятельство, что грунты деформируются не сразу после приложения нагрузки, а на это требуется определённое время?

Это связано с тем, что деформация грунта определяется изменением его пористости и для деформирования грунта нужно деформирование междучастичных связей. Эти связи часто бывают вязко-пластичными и деформируются не сразу, а с течением времени. Кроме того, в порах грунта содержится вода и изменение пористости, особенно полностью водонасыщенного грунта, связано с необходимостью отжатая воды из пор грунта, на что требуется время.

 

93. С какой скоростью в твердых телах распространяются напряжения?

Втвердых телах напряжения распространяются со скоростью звука.

 

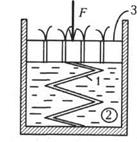
94. Какой представляется модель полностью водонасыщенного глинистого грунта? Что моделирует диаметр отверстий в поршне?

К. Терцаги предложил для полностью водонасыщенного глинистого грунта такую модель: цилиндр, заполненный водой, внутри которого имеется стальная пружина. Цилиндр закрыт поршнем, имеющим весьма малые отверстия. Если на этот поршень поставить груз, то опускание поршня возможно только за счет выдавливания из цилиндра лишней воды. Поршень начнет надавливать на пружину и остановится лишь тогда, когда все усилия груза полностью передадутся на пружину. При этом лишняя вода из цилиндра выдавится наружу. Диаметр отверстий моделирует фильтрационную способность грунта - чем мельче отверстия, тем медленнее выдавливается вода и медленнее идет процесс осадки .(см. рис.)

---

 



 

95. В чем заключаются предпосылки теории фильтрационной консолидации? Что представляет собою степень консолидации, на что она указывает, в каких пределах изменяется и какова ее размерность?

Предпосылки теории фильтрационной консолидации сводятся к следующему:

- скелет грунта линейно-деформируемый, деформируется мгновенно после приложения к нему нагрузки и вязкими связями не обладает;

- структурной прочностью грунт не обладает, давление в первый момент полностью передается на воду;

- грунт полностью водонасыщен, вода и скелет объемно несжимаемы, вся вода в грунте гидравлически непрерывна;

- фильтрация подчиняется закону Дарси.

Степень консолидации Uуказывает на то, какая часть полной осадкипроизошла к данному моменту времени. Степень консолидации безразмерна и изменяется от нуля (при t = 0) до единицы (при t =∞).

-

96. Какие напряжения вызывают сжатие грунта?

Только эффективные, то есть передающиеся на скелет грунта. Нейтральное давление на сжатие грунта не влияет.

97. Какие случаи изменения полного давления (эпюры напряжений σ_z) рассмотрены на практике и являются типовыми?

Рассмотрены три случая:

1) эпюра прямоугольная;

2) эпюра треугольная с вершиной вверху, у границы (имеется ввиду сжатие грунта от собственного веса);

3) эпюра треугольная с вершиной внизу и конечной ординатой вверху (эта эпюра соответствует способу эквивалентного слоя).

 

98. Какой порядок имеет уравнение фильтрационной консолидации и к какому типу дифференциальных уравнений оно принадлежит?

Уравнение Фурье линейное, второго порядка и параболического типа. Оно является уравнением, описывающим нестационарный процесс, так как содержит время.

 

99. В чем состоит метод Фурье решения уравнения теории фильтрационной консолидации?

Метод Фурье состоит в следующем. Поскольку основное уравнение линейное и содержит два переменных аргумента (координаты и время), то решением его будет сумма частных решений. Частные решения отыскиваются в виде произведения двух неизвестных функций - одной от координаты, другой от времени. В результате мы получаем уравнение, распадающееся на два обыкновенных дифференциальных уравнения, которые легко интегрируются. Дальнейшая задача связана с определением постоянных интегрирования исходя из граничных и начального условий.

---

Смотрите также файлы

• Методические рекомендации по эстетическому воспитанию младших школьников во внеурочной деятельности в области дпи заключение.pdf

• Занятие 4 Разработка базы данных Учет средств пожаробезопасности в среде Microsoft Access.docx

• 1. 2 Показатели расходов населения Дифференциация населения по денежным доходам и.docx

• Программа по истории России для 6 класса ( к умк н. М. Арсентьева, А. А. Данилов и др.) Пояснительная записка.docx

• Используем знания о возрастных особенностях пятиклассников, для этого необходимо ознакомится с теоретическими трудами в этой области следующих авторов таких как, Н. Н. Баранова, М. В. Григорьева, Д. А. Журавлев, Л. П.docx