Файл: Решение дифференциальных уравнений а б в г.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.01.2024

Просмотров: 328

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

  1. Найти общее решение системы дифференциальных уравнений .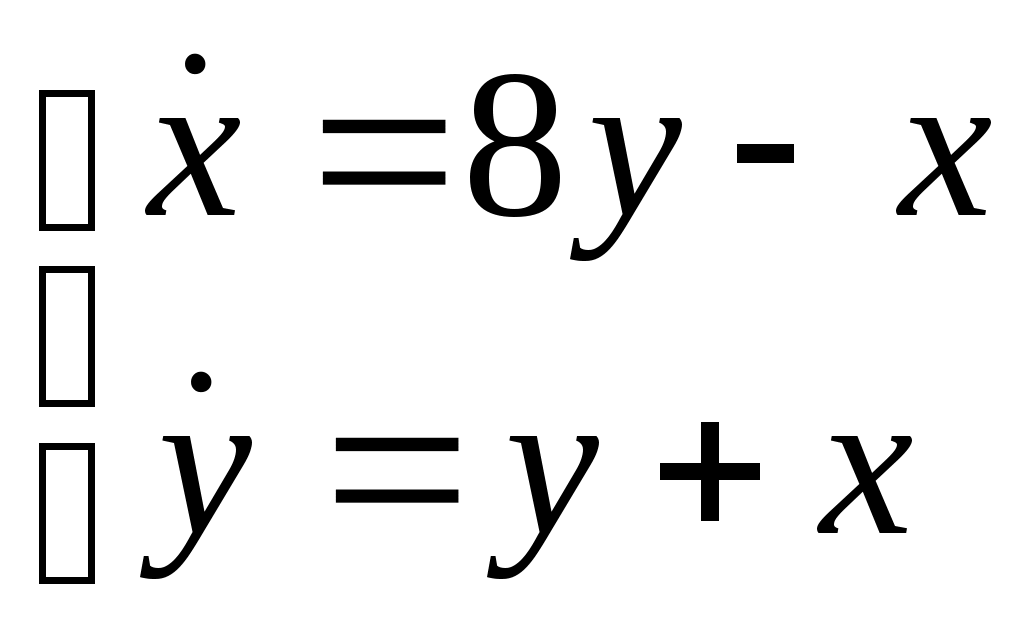

  1. Найти давление Р воздуха на высоте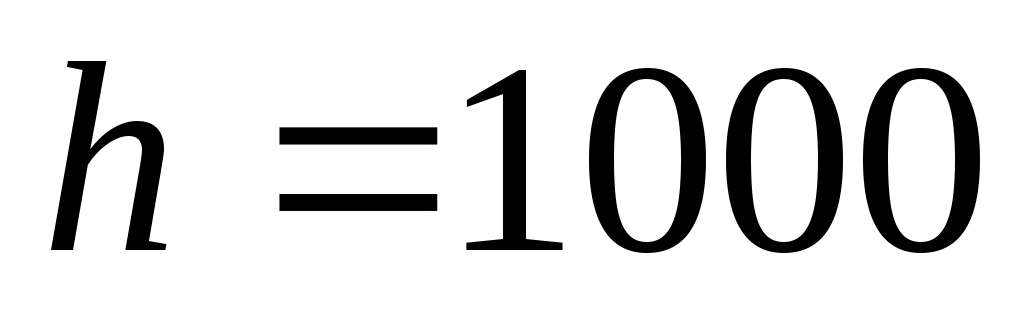 м, если известно, что давление воздуха равно 1 кг на 1 см2 над уровнем моря ( 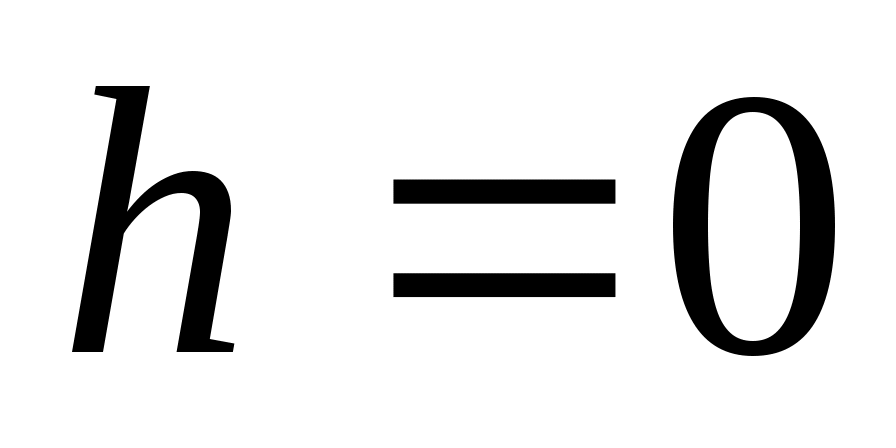) и 0,92 кг на 1 см2 на высоте 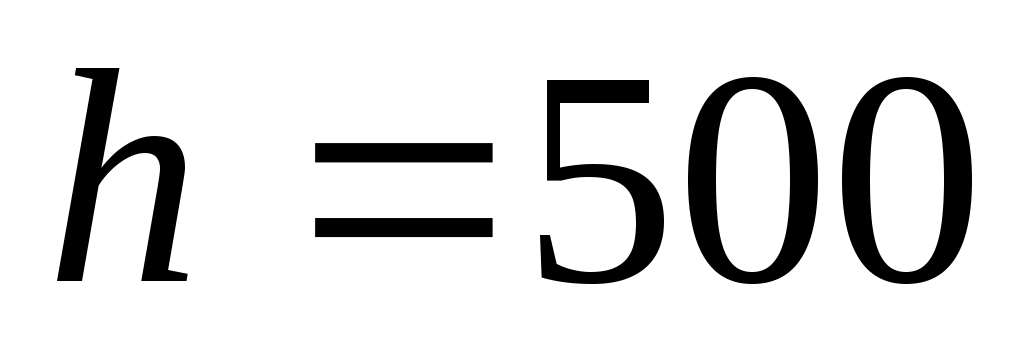м.

  1. Найти общее решение дифференциального уравнения .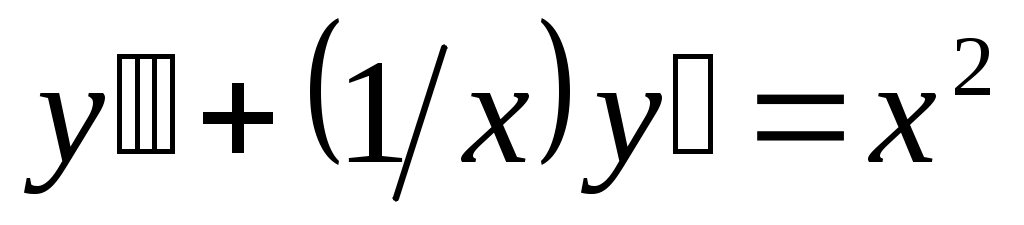

  1. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .
Вариант 16.

  1. Найти общее решение дифференциальных уравнений:

а) ;
в) ;

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям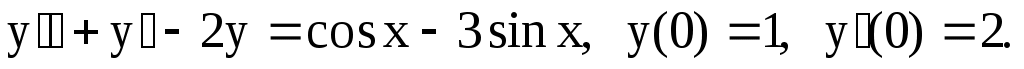

  1. Найти общее решение системы дифференциальных уравнений .

  1. Катер движется в спокойной воде со скоростью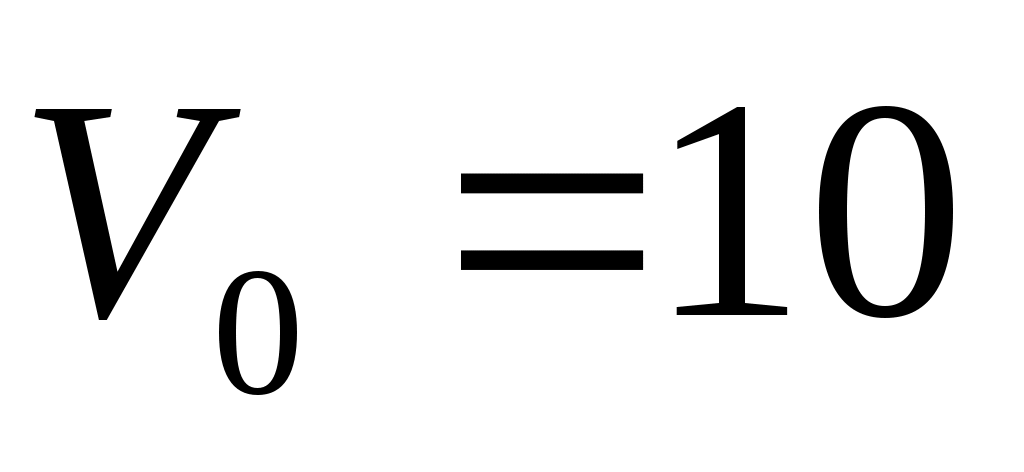 км/час. На полном ходу его мотор был выключен, и, через 2 мин, скорость катера уменьшилась до 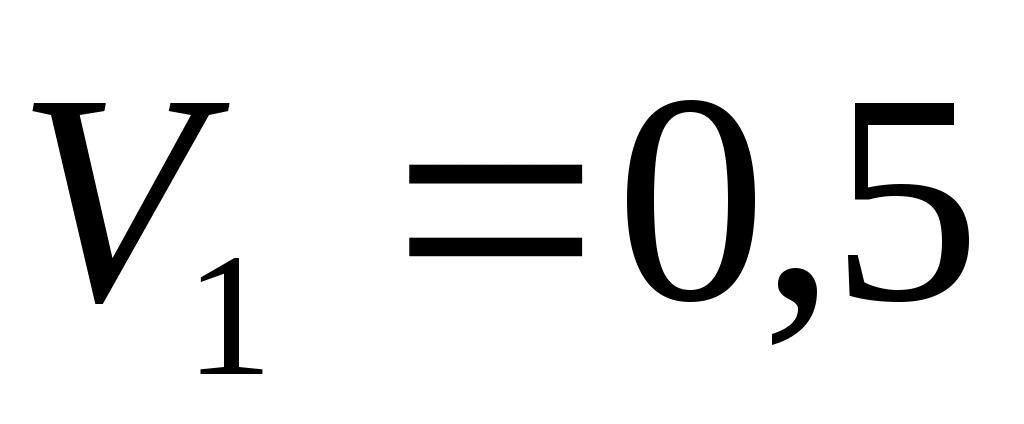км/час. Найти скорость, с которой двигался катер через 40 секунд после выключения мотора, считая, что сопротивление воды пропорционально скорости движения катера.

  2. Найти общее решение дифференциального уравнения .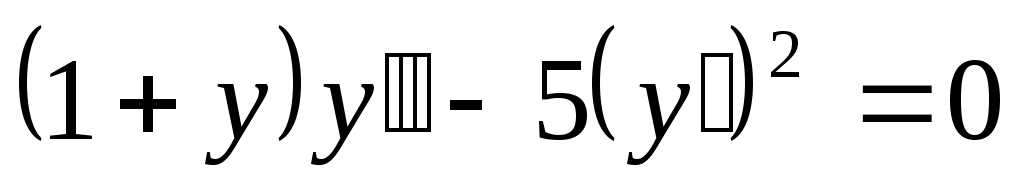

  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .
Вариант 17.

  1. Найти общее решение дифференциальных уравнений:

а) ;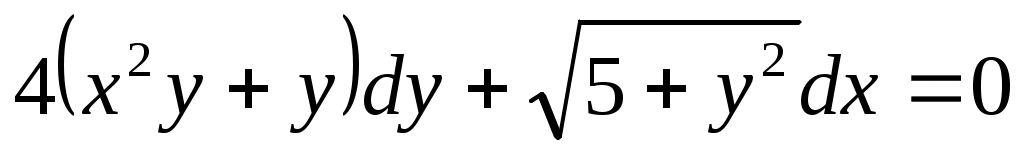
в) ;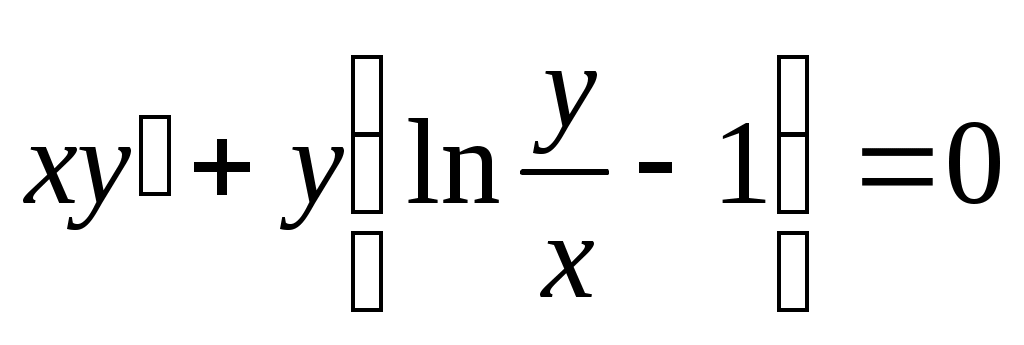

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям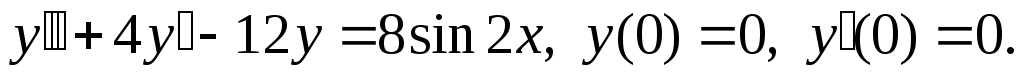

  1. Найти общее решение системы дифференциальных уравнений .

  1. Найти уравнение кривой, проходящей через точку A(3,1) и, обладающей тем свойством, что отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью ОУ.

  1. Найти общее решение дифференциального уравнения .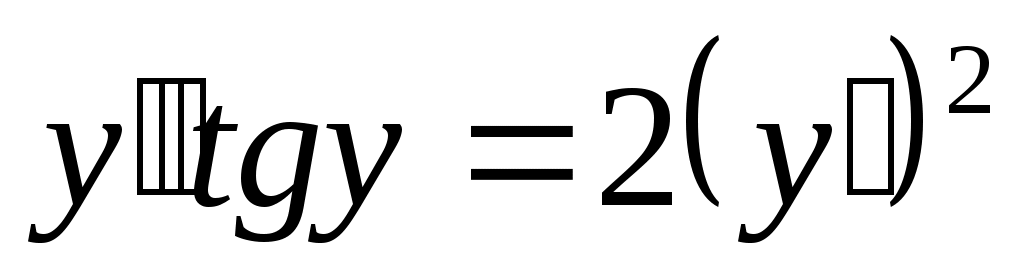

  1. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .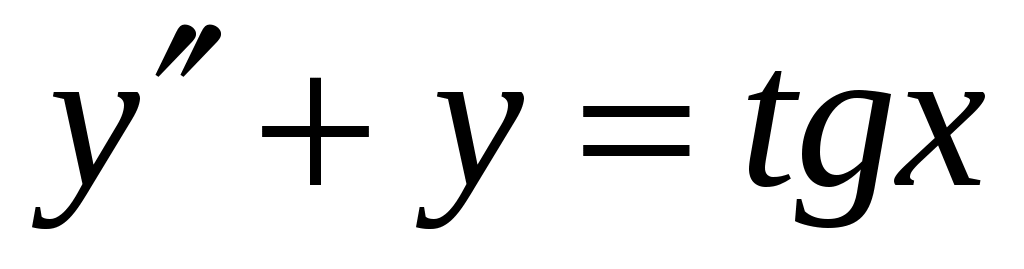
Вариант 18.

  1. Найти общее решение дифференциальных уравнений:

а) ;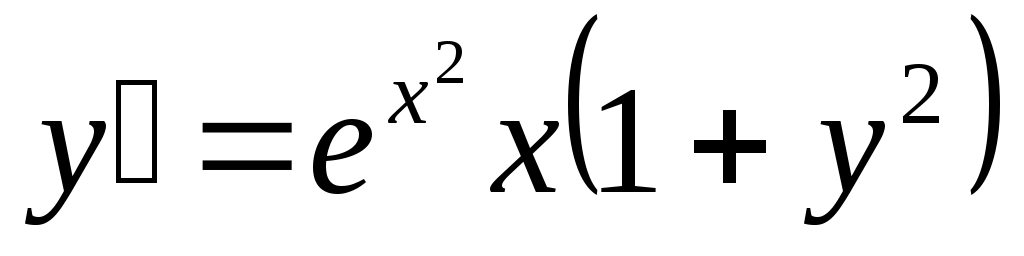
в) ;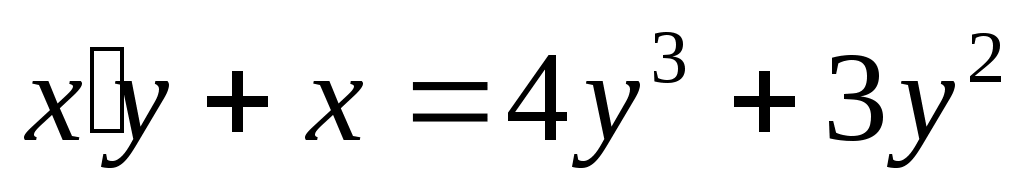

б) ;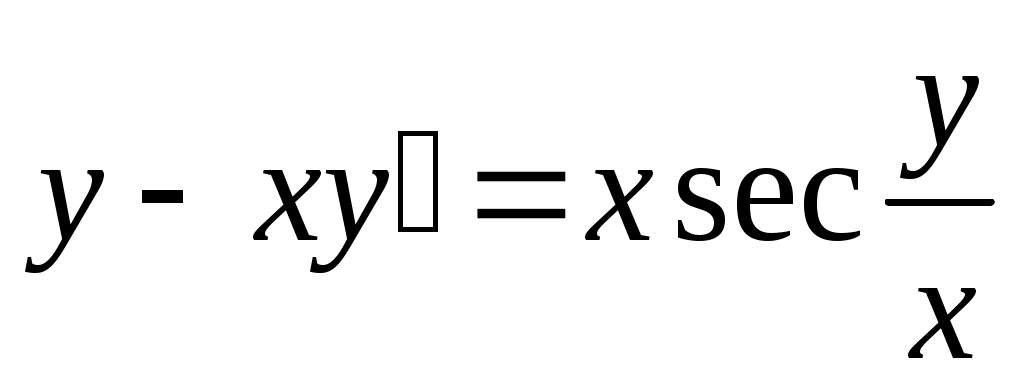
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям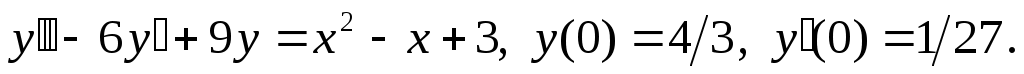

  1. Найти общее решение системы дифференциальных уравнений .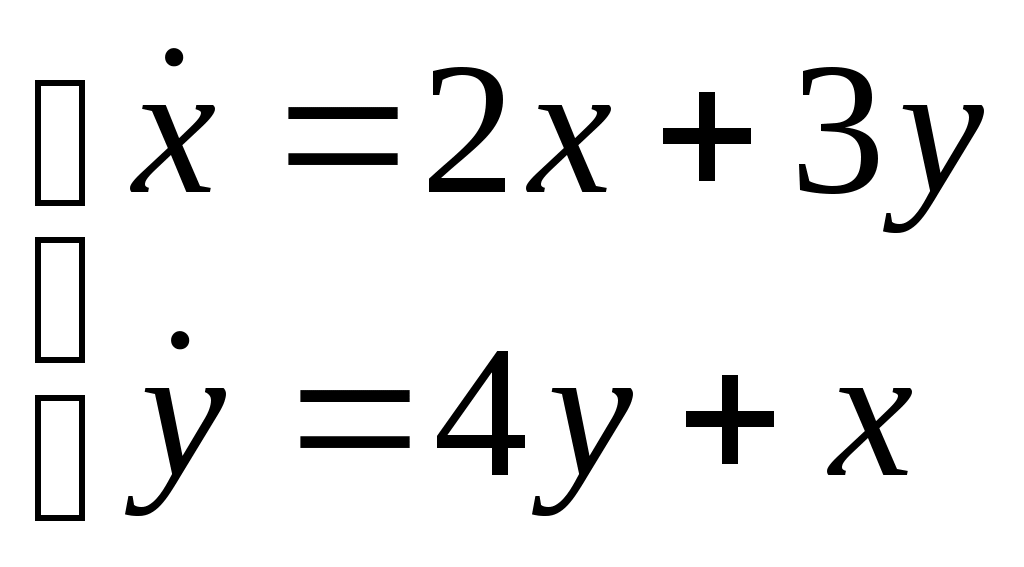

  1. Найти уравнение кривой, проходящей через точку B(1, 0) и, обладающей тем свойством, что отрезок, отсекаемый касательной на оси ОУ, равен радиус-вектору точки касания.

  2. Найти общее решение дифференциального уравнения .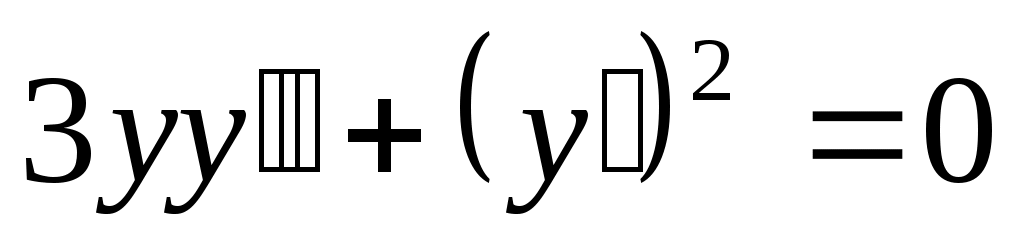

  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .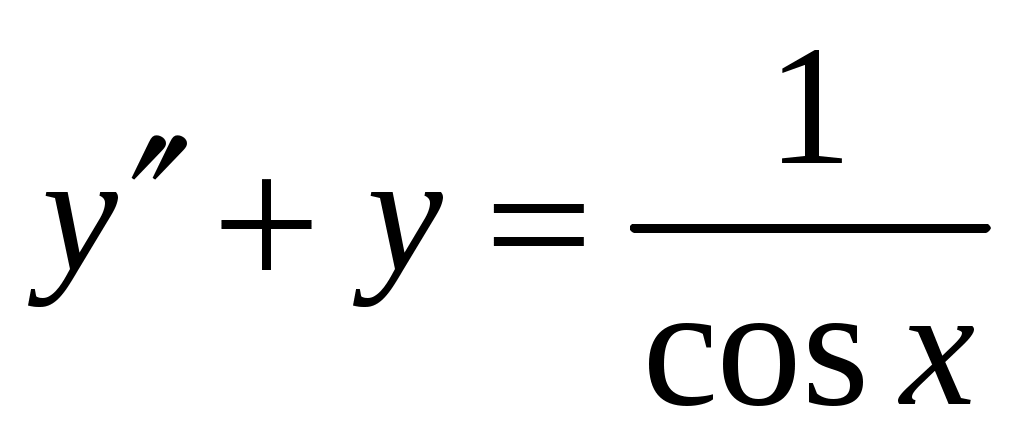
Вариант 19.

  1. Найти общее решение дифференциальных уравнений:

а) ;
в) ;

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям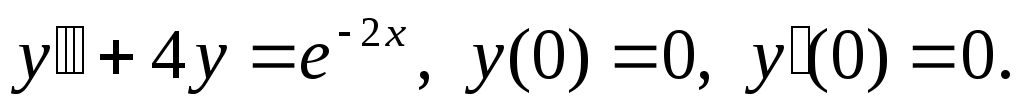

  1. Найти общее решение системы дифференциальных уравнений .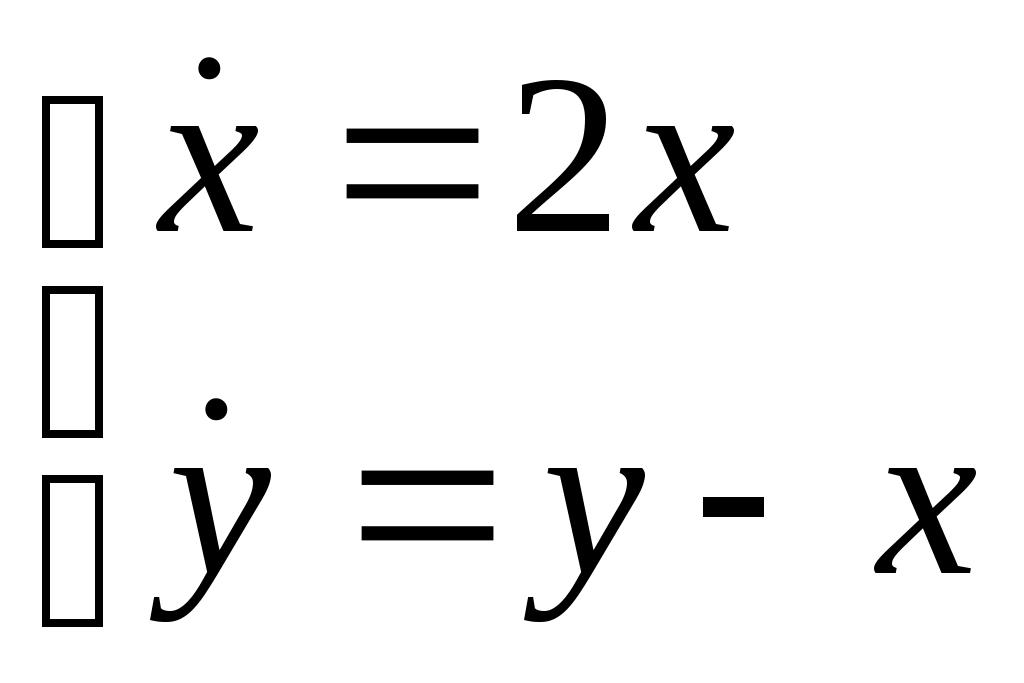

  1. Найти уравнение кривой, проходящей через точку B(1,1) и, обладающей тем свойством, что угловой коэффициент касательной в любой точке кривой вдвое больше углового коэффициента радиус-вектора точки касания.

  2. Найти общее решение дифференциального уравнения .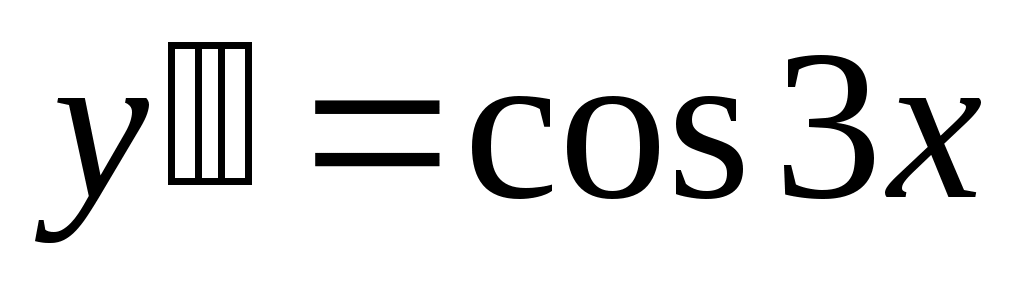

  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .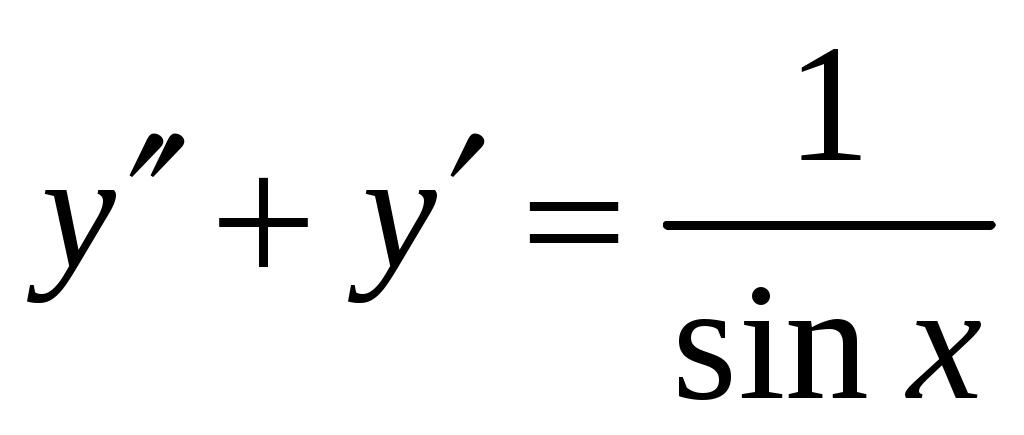
Вариант 20.

  1. Найти общее решение дифференциальных уравнений:

а) ;
в) ;

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям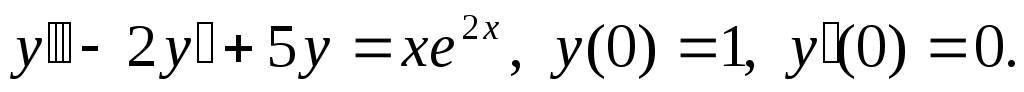

  1. Найти общее решение системы дифференциальных уравнений .

  1. Найти уравнение кривой, проходящей через т. A(1, 2) и обладающей тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен абсциссе точки касания.

  2. Найти общее решение дифференциального уравнения .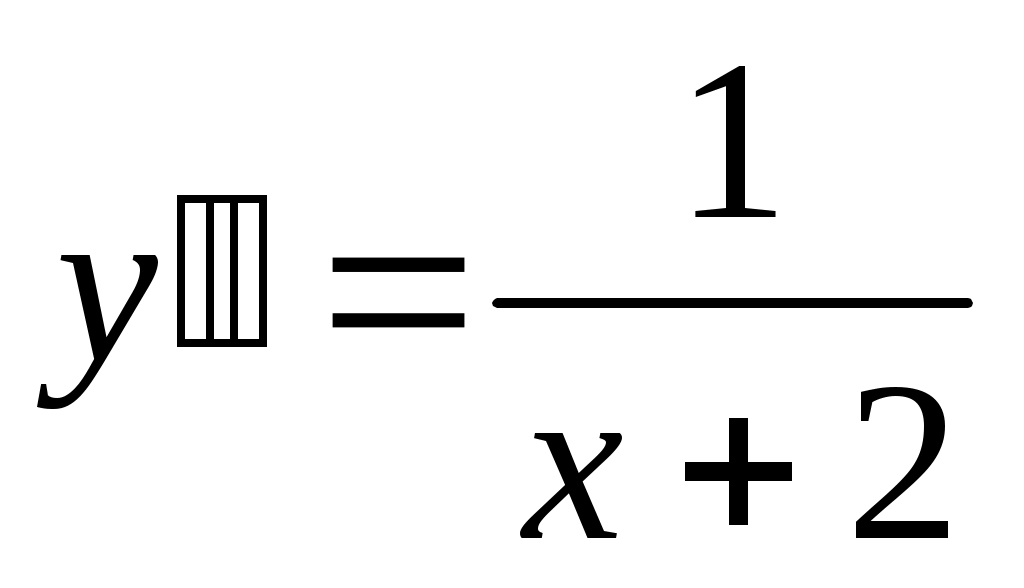

  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .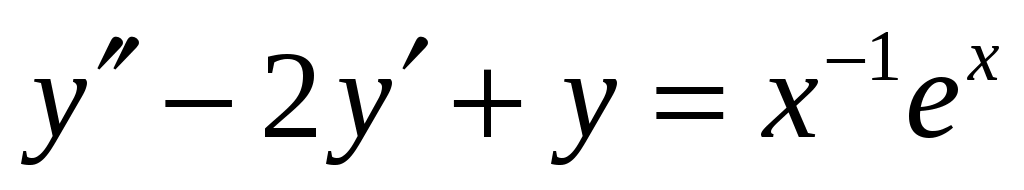
Вариант 21.

  1. Найти общее решение дифференциальных уравнений:

а) ;
в) ;

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям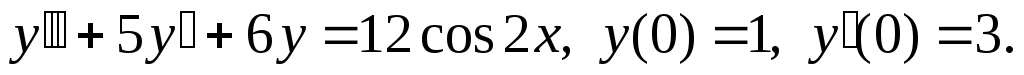

  1. Найти общее решение системы дифференциальных уравнений .

  1. Тело массой движется прямолинейно. На него действует сила, пропорциональная времени, протекшему от момента, когда (коэффициент пропорциональности 2). Кроме того, тело испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности 3). Найти скорость в момент 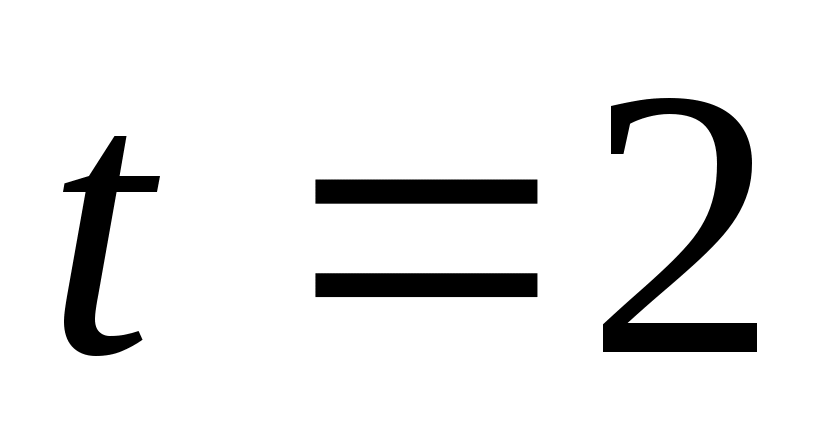сек.

  2. Найти общее решение дифференциального уравнения .

  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .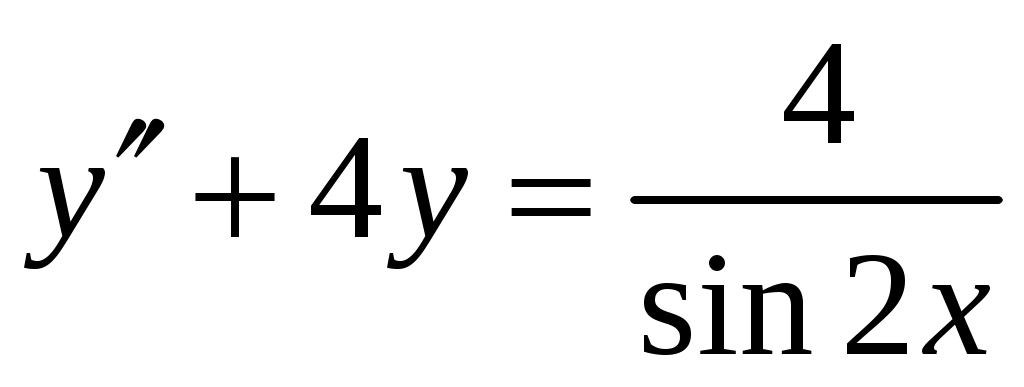
Вариант 22.

  1. Найти общее решение дифференциальных уравнений:

а) ;
в) ;

б) ;
г) .

  1. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям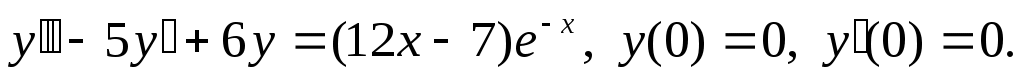

  1. Найти общее решение системы дифференциальных уравнений .

  1. Найти уравнение кривой, проходящей через т. A(-1,-1) и обладающей тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен квадрату абсциссы точки касания.

  2. Найти общее решение дифференциального уравнения .

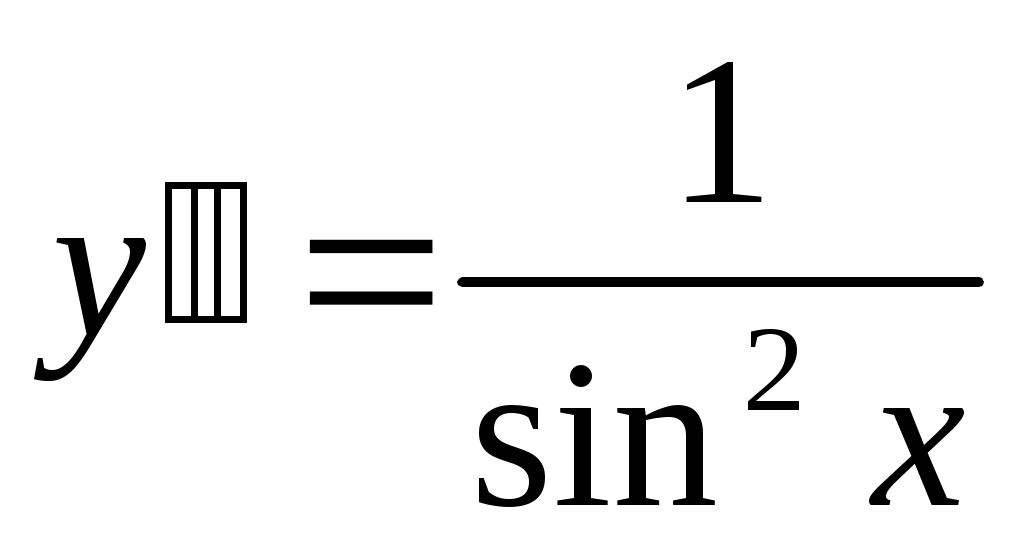  3. Найти общее решение дифференциального уравнения методом вариации произвольных постоянных .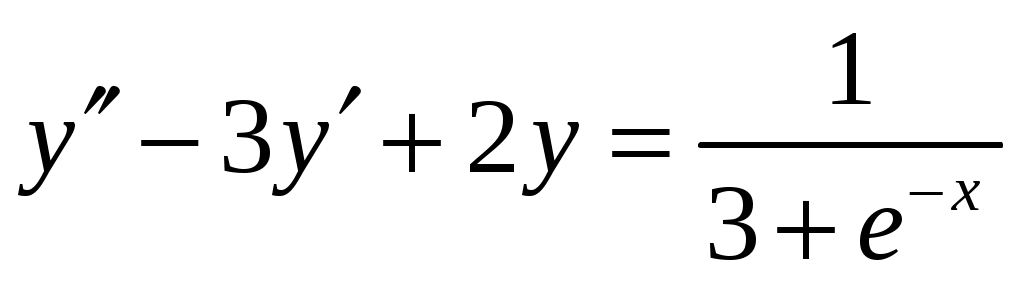

Смотрите также файлы