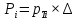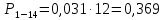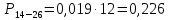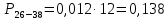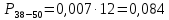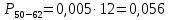Файл: Имеются данные об интервалах поступления автомобилей на базу строительных материалов. Интервалы поступления автомобилей даны в минутах. Требуется определить закон распределения случайной величины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.01.2024

Просмотров: 167

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание. Имеются данные об интервалах поступления автомобилей на базу строительных материалов. Интервалы поступления автомобилей даны в минутах. Требуется определить закон распределения случайной величины.

16
6
24
33
7
60
51
17
10
14
64
8
25
18
49
12
11
9

22
9
10
19
26
2
34
4
3
14
20
63
4
50
23
76
5
28

6
27
11
7
35
51
28
8
41
51
36
9
85
12
94
10
9
82

13
2
37
42
14
3
8
90
5
4
29
68
5
30
13
15
6
22

4
38
7
43
16
44
8
9
22
17
9
52
7
4
10
12
21
2
Решение. Полученный ряд значений случайной величины называется простым статистическим рядом. Обработка статистического ряда выполняется в следующем порядке: 1 Все данные располагаются в порядке возрастания или убывания значения случайной величины. Например, исходные данные можно расположить в порядке возрастания. Полученный ряд называется вариационным. Он уже дает некоторое представление об изучаемой случайной величине. Составим вариационный ряд:

2
2
2
3
3
4
4
4
4
4
5
5
5
6
6
6
7
7

7
7
8
8
8
8
9
9
9
9
9
9
10
10
10
10
11
11

12
12
12
13
13
14
14
14
15
16
16
17
17
18
19
20
21
22

22
22
23
24
25
26
27
28
28
29
30
33
34
35
36
37
38
41

42
43
44
49
50
51
51
51
52
60
63
64
68
76
82
85
90
94
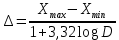
Данные вариационного ряда разбиваются на группы или классы. Эта операция, называемая табулированием или группировкой, выполняется для того, чтобы представить распределение в более компактной и наглядной форме. 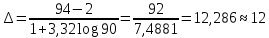Величину интервала групп предлагается определять по следующей формуле:где Xmax и Xmin – соответственно максимальное и минимальное значения в вариационном ряду;D – количество значений в вариационном ряду.В данном случае: Xmax=94, Xmin=2, D=90.Выбранные значения интервалов групп в порядке возрастания выписываются в таблицу 1. Некоторые значения могут значительно отличаются от остальных в вариационном ряду, в этом случае они признаются ложными и вычеркиваются из рассмотрения. Границы интервалов групп показываются черточками на вариационном ряду. Если значение находится на границе i-го и (i+1)-го интервалов, то значение учитывается в (i+1)-ом интервале. Необходимо отметить, что число групп (n) зависит от объема выборки, но для определения типа распределения случайной величины принимается обычно 10-12. Однако возможно принимать величину интервала групп условно, в зависимости от плотности распределения. По вариационному ряду подсчитывается число наблюдений в каждой группе mi. 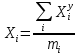Далее необходимо рассчитать среднее значение случайной величины в группе:где 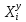– y-ый элемент i-ой группы; mi – количество наблюдений в группе i. 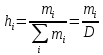Частота значений случайной величины в каждой группе определяется по формуле:Результаты показателей статистического распределения сводим в таблицу 1. Таблица 1 — Расчет показателей статистического распределения

Размер группы
Среднее в группе, Хi
Кол-во наблюдений в группе, mi
Частота появления события, hi
Xi×hi
(Xi – Xср)2 ×hi

2 – 14
7
41
0,456
3,367
128,896

14 – 26
19
18
0,200
3,767
5,784

26 – 38
31
11
0,122
3,811
5,939

38 – 50
43
6
0,067
2,856
23,119

50 – 62
53
6
0,067
3,500
53,351

62 – 74
65
3
0,033
2,167
55,458

74 – 86
81
3
0,033
2,700
107,499

86 – 98
92
2
0,022
2,044
102,119







∑mi=90
∑hi=1,000
∑(Xi×hi) = 24,211 = Xср
∑{(Xi – Xср)2 ×hi}= D[X]=482,164
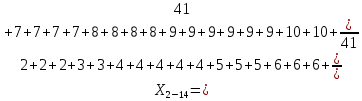
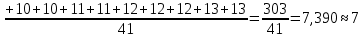
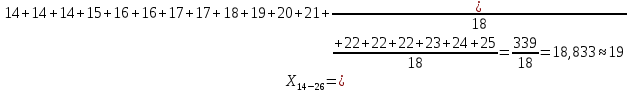
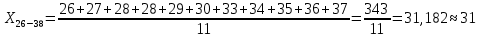
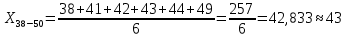
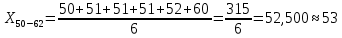
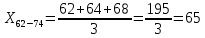
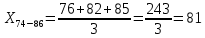
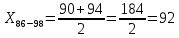
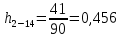
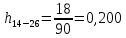
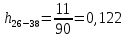
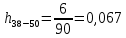
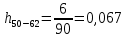
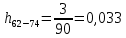
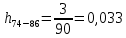
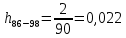
Среднее в группе, Хi:Частота появления события, hi:Xi×hi:X2-14×h2-14=7×0,456=3,367X14-26×h14-26=19×0,200=3,767X26-38×h26-38=31×0,122=3,811X38-50×h38-50=43×0,067=2,856X50-62×h50-62=53×0,067=3,500X62-74×h62-74=65×0,033=2,167X74-86×h74-86=81×0,033=2,700X86-98×h86-98=92×0,022=2,044(Xi – Xср)2×hi:(X2-14– Xср)2×h2-14=(7–24,211)2×0,456=128,896(X14-26– Xср)2×h14-26=(19–24,211)2×0,200=5,784(X26-38– Xср)2×h26-38=(31–24,211)2×0,122=5,939(X38-50– Xср)2×h38-50=(43–24,211)2×0,067=23,119(X50-62– Xср)2×h50-62=(53–24,211)2×0,067=53,351(X62-74– Xср)2×h62-74=(65–24,211)2×0,033=55,458(X74-86– Xср)2×h74-86=(81–24,211)2×0,033=107,499(X86-98– Xср)2×h86-98=(92–24,211)2×0,022=102,119Числовые характеристики, определяемые по выборке, являются приближенными оценками соответствующих характеристик генеральной совокупности. Оценки любого параметра должны быть: состоятельными, т.е. при увеличении числа объектов D сходиться по вероятности к соответствующим параметрам генеральной совокупности, несмещенными, т.е. чтобы при оценке параметра по выборке не делалось систематической ошибки в сторону увеличения или уменьшения параметра, и эффективными, т.е. чтобы они имели наименьшую дисперсию.
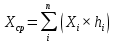
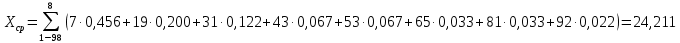
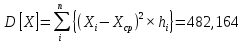
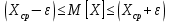
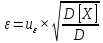
Всем этим требованиям удовлетворяет выборочное среднее, определяемое по формуле:Выборочная дисперсия определяется по формуле:Надежность и точность оценок определяется доверительным интервалом для выборочного среднего:где ε – величина отклонения, которая определяется по следующей формуле:где uε – величина, определяемая для принятого уровня значимости P∆ при числе наблюдений ≥ 20 по таблицам функции Лапласа, в нашем случае при P∆=0,05, uε=1,96, тогда: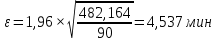Таким образом, доверительные границы равны: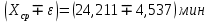Интенсивность потока определяется по следующей формуле: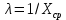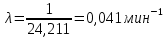Вероятность появления в одной точке: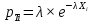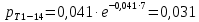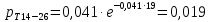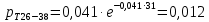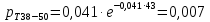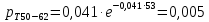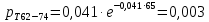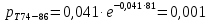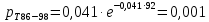Вероятность появления в группе:

Смотрите также файлы