Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра физики

 

МЕХАНИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО. ДВИЖЕНИЯ.

 

 Методические указания к выполнению

лабораторных работ

 для студентов всех форм обучения всех специальностей

 

СОСТАВИТЕЛИ: Т.С. Байпакбаев, М.Ш.Карсыбаев, А.М.Саламатина.  Механика поступательного и вращательного движения. Методические указания к выполнению лабораторных работ для студентов всех форм обучения всех специальностей.

 

Методические указания содержат описания девяти лабораторных работ, в которых изложена методика лабораторного эксперимента, описаны экспериментальные установки, указаны порядок проведения эксперимента и обработки результатов и контрольные вопросы.

       Методические указания предназначены для студентов всех специальностей и всех форм обучения.

 

Введение

Физика непосредственно связана с экспериментом. Это значит, что все физические   законы   устанавливаются   и   проверяются   путем   накопления   и сопоставления экспериментальных данных.

Физический практикум призван помочь студентам глубже осознать основные физические закономерности и приобрести элементарные навыки экспериментирования, научить анализировать результаты эксперимента и оценивать их точность. Практикум является введением в дальнейшую самостоятельную работу будущего инженера.

Приступая к выполнению лабораторной работы, следует ознакомиться с теорией данного вопроса, используя для этого указанные учебники по физике и физпрактикуму, внимательно прочесть методические указания к работе, ознакомиться с приборами, которые используются.

         Успех эксперимента в значительной мере зависит от правильной записи результатов.  С этой целью для работы в лаборатории необходимо  иметь специальную тетрадь, в которой записывается название, цель и задачи работы, краткий конспект. Полезные советы для начинающих экспериментаторов вы найдете в литературе [2].

         Выполнение работ в физической лаборатории, как известно, включает три этапа: подготовка к эксперименту, проведение эксперимента и оформление отчета. На подготовительном этапе необходимо:

а) ознакомиться с целями и задачами;

---

б) уяснить теоретическое обоснование тех явлений и процессов, взаимосвязей и закономерностей, которые лежат в основе эксперимента;

в) составить план действий;

г) подготовить таблицу для записи результатов эксперимента.

         В результате подготовительной работы у студента должно сформироваться достаточно ясное представление о предстоящем эксперименте и ожидаемых результатах.

         Проведение экспериментов начинают с установки приборов, затем производят наблюдение и отсчет измеряемых величин; полученные результаты записывают в таблицы. На заключительном этапе выполняют обработку результатов, вычисления искомых величин и оценку погрешностей. Приступая к вычислениям, необходимо руководствоваться правилами действий с приближенными числами. Наконец, по результатам выполненной работы необходимо сформулировать выводы.

В экспериментальной физике часто пользуются графиками для разных целей. Во-первых, для наглядности и сравнения с другими результатами или с теоретической кривой; во-вторых, для определения некоторой величины (напр., по наклону графика или по отрезку, отсекаемому, графиком от какой-либо из осей и т.д.); в-третьих, для градуировки прибора. Построение графиков должно удовлетворять ряду требований, которые подробно изложены в литературе [1,2].

1 Статистическая обработка результатов измерений

1.1 Основные понятия и определения

Проведение физического эксперимента, как правило, с измерением той или иной физической величины. Измерения принято различать прямые, когда измеряется сама исследуемая физическая величина, икосвенные, когда значение искомой величины находят на основании известной зависимости от величин, получаемых прямыми измерениями. Всякому измерению присущи всякие погрешности, поэтому в опытах мы вместо истинного значения измеряемой величины Х₀,получаем некоторое приближенное значение X.Разность между результатом измерения и истинным значением называется абсолютной погрешностью измерения       ∆Х = Х-Х₀.       Всевозможные ошибки измерений по характеру происхождения можно разделить на три типа.

Систематические погрешности обусловлены одной и той же причиной. 

---

Поэтому при повторении опыта они обычно имеют одно и то же значение и знак, т.е. систематически повторяются. Они являются следствием несовершенства приборов и недостатков методики измерения. Систематические погрешности можно учесть с помощью поверки приборов и уменьшить, усовершенствовав методику измерений.

Случайные погрешности являются следствием случайных неконтролируемых помех, влияние которых на процесс измерения учесть невозможно. Они связаны с ограниченной точностью приборов, ограниченной чувствительностью наших органов чувств, изменением внешних условий и т.д. Случайные погрешности устранить нельзя, но благодаря тому, что они подчиняются вероятностным закономерностям, при достаточно большом числе измерений, всегда можно указать пределы, внутри которых заключается истинное значение.

Промахи - это, очевидно, ошибочные измерения или наблюдения, возникающие в результате небрежности экспериментатора. При вычислениях такие данные следует отбрасывать и проводить повторные измерения.

Случайные ошибки при многократном повторении опыта служат причиной разброса результатов отдельных измерений. Предположим, что мы п раз измерили некоторую величину, истинное значение которой равно а.

Из-за случайных ошибок мы вместо а получим ряд значений Х_1… Х₂... X_i,...X_n. Какое из этих измерений ближе всего к истинному, мы не знаем. Самой лучшей оценкой по данным измерениям является среднее арифметическое <Х>из числа всех измерений

                                            =  .                                         (1)

Так как среднее значение является приблизительной оценкой истинного значения, то нужно уметь оценивать абсолютную величину возможного отклонения среднего результата от истинного значения. Это отклонение  Х называется абсолютной ошибкой среднего

     ΔX=|­ a|.                                             (2)

Среднее значение и абсолютная ошибка ΔХсреднего определяют, так называемый, доверительный интервал (< X > ± ΔХ), в пределах которого, по данным опыта, заключена измеряемая величина а.

Например, результат измерения скорости звука записав так:

V = (335 ±5) м/с.

Эта запись означает, что скорость звука, по данным опыта, лежит в пределах от 330 м/с по 340 м/с.

Однако и такое утверждение не может считаться абсолютно достоверным. Необходимо указать надежность получаемого результата. Надежность результата оценивается так называемой доверительной вероятностью Р.

Доверительная вероятность - это вероятность того, что истинное значение измеряемой величины попадает в найденный доверительный интервал.

Предположим, что в приведенном выше примере доверительный интервал найден с доверительной вероятностью Р, равной 0, 95. Это значит, что 95 измерений из 100 попадут в найденный интервал и лишь 5 окажутся за его пределами. Чем уже доверительный интервал (т.е. чем меньше абсолютная ошибка ΔХ)при заданном значении доверительной вероятности, тем точнее выполнены измерения. Точность измерений выявляется при сравнении абсолютной ошибки измерений со средним значением всех измерений путем вычисления так называемой относительной ошибки.

Относительная ошибка вычисляется по формуле

%.

В рассмотренном примере со скоростью звука она равна:

.

Итак, измерения любой физической величины должны завершаться указанием доверительного интервала с заданной доверительной вероятностью и вычислением относительной ошибки измерений.

 

1.2 Определение доверительного интервала на основании нормального закона распределения случайной величины

Доверительный интервал и доверительная вероятность обосновываются теорией погрешностей измерений, в основе которой лежит нормальный закон распределения случайной величины. Эта теория учитывает лишь случайные ошибки. 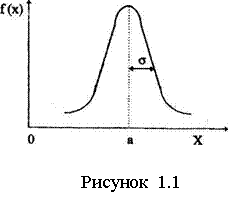 На рисунке 1.1, где представлен общий вид нормального распределения, видно, что основная масса результатов измерения группируется около центра а. Отклонения по обе стороны от центра распределения наблюдаются тем реже, чем больше абсолютная величина (х - а)таких отклонений. Степень разброса отдельных измерений относительно а определяет другой параметр функции распределения, параметр σ. Анализ функции распределения показывает, что на расстоянии  <σ от центра распределения кривая имеет точки перегиба и при |х - а | > σ функция быстро стремится к нулю. Величина <σ²>, называемая дисперсией, совпадает со средним значением квадратов отклонений результатов отдельных измерений от истинного значения, т.е. <σ²>= <(х-а)² >. Поэтому параметр σ называют стандартом отклонения или средним квадратным отклонением; σопределяет также максимальное значение функции распределения, которое достигается при х=а и равно    σ= . Отсюда видно, чем меньше σ, тем выше максимум. На одном и том же графике площади под кривыми распределения, соответствующие различным значениям σ, должны быть одинаковы (равными 1),  поэтому на графике кривые с меньшим значением σ выглядят более узкими и высокими, чем кривые с большим σ.

На рисунке 1.2 приведены две нормальные кривые, где σ₂>σ₁. При измерениях величина зависит от точности избранного метода, чем точнее метод, тем меньше σ. Доверительный интервал всегда выбирается симметричным относительно а, тогда доверительная вероятность определяется интегрированием (смотри выражение 4) нормального закона распределения (1.5) в пределах от (а - ΔХ )до (а + ΔХ).

Если полуширину интервала  Х брать кратной σ, то, как показывают соответствующие расчеты, для ΔХ=σ  доверительная вероятность равна Р=0,683, для ΔХ=2σ  Р=0,954, а для ΔХ=3σ Р=0,997. При производстве измерений а и σ неизвестны. Поэтому при математической обработке результатов измерений необходимо получить по этим результатам наилучшую оценку а и σ.                                                                                                             Лучшей оценкой а является среднее арифметическое <X> из всех измерений (1). Можно показать, что при большом числе измерений (n→∞)          = а, т.е.           .

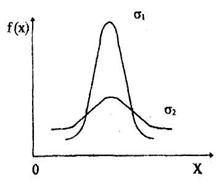Лучшей оценкой  σ является выборочное среднее квадратичное отклонение S_n, равное 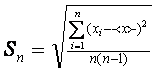    .                              (3)

 При  n→∞     S_n   и σ совпадают,  т.е.     .                                                                                                              

                                                                                                                                             Рисунок 1.2

При большом числе измерений (n>20) результат обрабатывают, пользуясь правилом "трех сигм". По формуле (1) находят <X>,по формуле (3) вычисляют выборочное среднеквадратичное отклонение S_n  и принимая его равным 3σ, записывают доверительный интервал в виде

                        Х = <Х>±Зσ,  

доверительная вероятность в этом случае равна 0,997.

В лабораторном практикуме, когда производится небольшое число измерений (n<10), широко пользуются методом, разработанным Стьюдентом. Этот метод называется методом малых выборок. В этом случае в качестве стандарта отклонения средней величины от истинного значения принимается величина S, называемая средним квадратичным отклонением среднего и равная

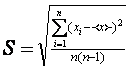    .                                                        (4)

Следует заметить, что величину S часто обозначают через   и также называют среднеквадратичным отклонением (среднеквадратичной погрешностью среднего). Доверительный интервал записывается в виде

                        Х= <Х>± Х,

причем                          Х = t·S                                                               (5)

          где ț - коэффициент Стьюдента.

        Коэффициенты Стьюдента зависят от выбранного значения доверительной вероятности Р и числа произведенных измерений п. Эти коэффициенты рассчитываются в теории вероятностей и приводятся в справочных таблицах.

Таблица 1.1- Таблица коэффициентов Стьюдента

n	0,6	0,7	0,95	0,99
2	1,38.	2,0	12,71	63,66
3	1,06	1,3	4,30	9,92
4	0,98	1,3	3,18	5,84
5	0,94	1,2	2,78	4,60
6	0,92	1,2	2,57	4,03
7	0,90	1,1	2,45	3,71
8	0,90	1,1	2,36	3,50
9	0,90	1,1	2,31	3,36
10	0,88	1,1	2,26	3,25

Следует заметить, что при большом числе измерений метод Стьюдента дает тот же результат, что и при использовании нормального закона. Однако для малого числа измерений доверительный интервал по методу Стьюдента вычисляется более надежно.

1.3 Порядок обработки результатов измерений по методу малых выборок

Обработку результатов измерений по методу малых выборок следует производить в таком порядке:

а) произвести п измерений (X₁, X₂,..., X_i,... X_n);

б) найти среднее арифметическое по формуле

                                

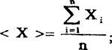
в) определить отклонение каждого измерения от среднего ∆X_i=|‌‌X_i–‌| (прямые скобки указывают на то, что нас интересуют лишь абсолютные значения указанных разностей);

г) определить стандарт отклонения

                              ;

                              

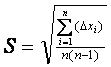д) по таблице коэффициентов Стьюдента найти t;

е) определить абсолютное значение случайной ошибки среднего арифметического

∆X = t·S;

ж) определить относительную ошибку

Е =  ∙100%; 

и) записать окончательный результат в виде:                                        для   Р = 0,95           Х = <Х>± Х,    Е = А%.

При записи окончательного результата нужно иметь ввиду следующее. Так как абсолютная ошибка ΔХсама определяется с ошибкой, то ее следует округлять до первой значащей цифры. Лишь в том случае, когда первая значащая цифра ошибки меньше 4, в результате можно оставлять 2 значащие цифры. Например, в результате вычислений было получено  Х=0,524. Следует оставить  Х=0,5. Ошибку  Х=0,167 можно округлить так:  Х=0,20 или  Х=0,17.

Абсолютная ошибка показывает, в каком разряде полученного результата содержится неточность, поэтому результат нужно округлять до того разряда, в котором находится значащая цифра ошибки. Например, мы получили     < X > = 26,731 и  Х=0,8. Значит, ответ нужно записать так:

X = 26,7 ± 0,8;

или получив < X> = 0,8568 и  Х=0,014, записываем:

 Х = 0,857± 0,014.

 

1.4 Классы точности приборов

Для характеристики измерительных приборов часто используют понятие класса точности.

Классом точности прибора γ называется наибольшая допустимая относительная приведенная погрешность, определяемая по формуле

γ = ·100%                                                              (6)

где ΔA – наибольшая допустимая абсолютная погрешность прибора;

A_пред – предельное (номинальное) значение измеряемой величины по шкале прибора.

Класс точности приборов в соответствии со стандартом может принимать следующие значения: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4.

Класс точности прибора указывается на его шкале. Если на шкале такого обозначения нет, это означает, что прибор внеклассный, то есть его приведенная погрешность превышает 4%.

Зная класс точности можно вычислить наибольшую допустимую абсолютную погрешность прибора (которую принимают одинаковой на всей шкале прибора) по формуле 

  ΔA= .                                                                (7)

2 Лабораторная работа ММФ-1. Измерительный практикум

Цель работы: овладение методикой измерения физических величин и методами обработки результатов измерений на примере удельного сопротивления провода.

Задачи:     - измерить сопротивление провода и изучить зависимость  сопротивления

R провода от его длины ℓ;

- определить удельное сопротивление ρ материала провода;

- провести обработку результатов измерений методом малых выборок.

 

2.1 Методика эксперимента

Сопротивление проводников зависит от их формы, размеров и материала, из которого они изготовлены, т.е.   R =  . Если проводник имеет форму круглого цилиндра постоянного поперечного сечения  S= ,  тогда его сопротивление равно                                                                                                                               R=                                                                    (1)                где ℓ  - длина проводника;                                                                               d - его диаметр;                                                                                                ρ- удельное сопротивление.                                                                    Из (1) легко получить формулу

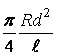ρ=                                                            (2)

которая является расчетной в данной работе.                                                 Значение сопротивленияR рассчитывается по показаниям амперметра и вольтметра (расчетные формулы представлены ниже).

Для более точного определения сопротивления необходимо учитывать



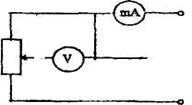внутреннее сопротивление электроизмерительных приборов – амперметра R_A  и вольтметра R_v.

                    а)                                                                     б)

Рисунок 2.1

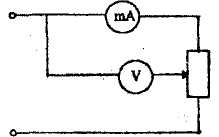
На рисунке  2.1  показаны две возможные схемы: а) и б) - включения  приборов, которые выбираются произвольно с помощью переключателя.

При включении схемы а) сопротивление следует находить по формуле

R=                                             (3)

гдеR_A = 0,15 Ом - внутреннее сопротивление амперметра;                                      U и  I - показания вольтметра и амперметра соответственно.

Если включена схема б), то в этом случае сопротивление находится по формуле

                                                R= 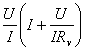                              (4)

где R  = 2500 Ом – внутреннее сопротивление вольтметра. Обе формулы можно получить из закона Ома.

 

2.2 Экспериментальная установка

Установка     РРМ-01     предназначена     для     определения     удельного сопротивления провода (рисунок 2.2).

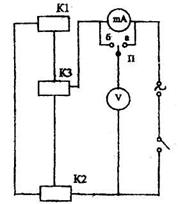Между двумя неподвижными контактами К1 и К2 закреплен исследуемый    провод.    С    помощью подвижного контакта К3 устанавливается необходимая длина провода, на которой измеряется падение напряжения и ток. Схема включения (а) или (б) выбирается переключателем П.

 

 

 

 

 

Рисунок 2.2                   

 

2.3 Порядок выполнения работы

         2.3.1 Зафиксировать положение верхнего контакта и записать в таблицу 1
длину   провода (не менее половины всей длины), заключенного между нижним и    средним контактами.                                                                                                                           2.3.2 С помощью микрометра измерить диаметр провода Д.

         2.3.3 Включить установку, переключателем П выбрать схему включения   приборов.

         2.3.4 Для различных (не менее 5) значений длины провода   провести десять измерений напряжения U и силы I тока.

Таблица 2.1

d, м

, м

U,  B

I, А

R, Ом

,Ом ·м

< >, Ом·м

< >-

 

2.4 Обработка результатов

          2.4.1 В зависимости от выбранной схемы по формуле (3) или (4) вычислить активное сопротивление провода.

         2.4.2 Построить график зависимости сопротивления провода  R от его длины ℓ.

         2.4.3 По формуле (2) вычислить значение удельного сопротивления  .

          2.4.4 Для   всех   измерений   по   формуле   [(2),   см.   Введение]   найти среднеквадратичную погрешность S и величину доверительного интервала  =2 S  (для вероятности Р=0,95).

         2.4.5 Выбрать любые три измерения, найти значение интервала 
 методом малых выборок.

         2.4.6 Для  n=10 и n=3 найти относительную погрешность соответствующего среднего арифметического.

         2.4.7 Вычислить относительную приборную погрешность любого единичного измерения по формуле

.

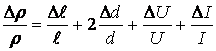         2.4.8 Сравнить абсолютные и относительные погрешности, проанализировать полученные результаты и сформулировать выводы.

2.5 Контрольные вопросы                                                                                                         2.5.1 Прямые   и   косвенные   измерения,   систематические   и   случайные погрешности.

         2.5.2 Абсолютная и относительная погрешности. Класс точности приборов.

         2.5.3 Доверительный интервал и доверительная вероятность.

           2.5.4 Обработка результатов прямых и косвенных измерений.

         2.5.5 Методика проведения работы.


 

3 Лабораторная работа ММФ  - 2. Изучение законов кинематики и

динамики на машине Атвуда

 Цель работы: изучение законов равномерного и равноускорен­ного движение, а также второго закона Ньютона

Задачи:    

- проверить формулы равномерного и равноускоренного движения;

           - проверить второй закон Ньютона.

3.1 Методика эксперимента

Движение системы, состоящей из двух грузов с массами т и т + т  связанных нерастяжимой нитью, и блока радиуса r с моментом инерции описывается законами динамики. Ведь грузы одинаковы,  то потенциальная энергия системы не зависит от высоты поднятия грузов, т.к. убыль потенциальной  энергии одного из них приводит к возрастанию энергии другого. Когда же грузы различны, изменение потенциальной энергии системы определяется изменением положения   перегрузка т

                                                          (1)

где     h - изменение положениия перегрузка.

Потенциальная энергия системы превращается в кинетическую энергию поступательного и вращательного движения (работой по преодолению сил трения можно пренебречь). 

 

                                       (2)

где    - кинетическая энергия груза без перегрузка;

- кинетическая энергия груза с перегрузком  и   - кинетическая энергия   вращательного движения блока.

Учитывая, что  h=     вращения диска    и линейная скорость  V = at, можно получить выражение для определения ускорения системы

                                           а= .                                          (4)

Если пренебречь моментами инерции блока 1, формула примет вид

                   a=                                                (5)

где М = 2m + m  - полная масса системы;                                                      m  - масса перегрузка. После снятия перегрузка грузы будут двигаться равномерно со скоростью V, которая при неизменном  расстоянии S останется постоянной, тогда

   V

---

= .                                      (6)

При равноускоренном движении без начальной скорости ускорение

  a=                                                               (7)

где V - конечная скорость, которая равна скорости равномерного движения и, следовательно, может быть найдена по формуле V = h /t. Тогда окончательное выражение для определения ускорения запишется в виде

                                    a= .                    (8)

Одним из способов проверки второго закона Ньютона является  проверка соотношения (5), для этого полная масса системы М должна оставаться постоянной, а величина действующей  силы – изменяться

                                           =                                 (9)

где m_1, m_{2 …,}m - массы перегрузков.

3.2  Описание экспериментальной  установки

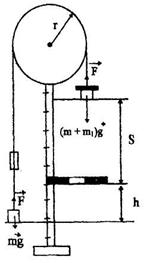
Машина Атвуда РРМ-2 состоит из вертикальной колонны с масштабной линейкой, на которой закреплены три кронштейна (рисунок 3.1). На колонне установлен легкий блок, способный вращаться с незначительным трением,  и электромагнит. Через блок перекинута  легкая нить с прикрепленными на концах грузами одинаковых масс.                                                                             Электромагнит удерживает блок с грузами в состоянии покоя. Средний кронштейн снабжен кольцом для снятия перегрузка. В момент

---

прохождения груза через кольцо включается секундомер, измеряющий время равномерного движения грузов t.                                                                                                     Измеряя расстояние, пройденное грузом соответственно при равноускоренном S и равномерном движенииh , а также время t, можно проверить основные законы кинематики и динамики поступательного движения, а также вычислить ускорение свободного падения.

 

3.3 Порядок выполнения работы

Упражнение 1. Проверка формулы равномерного

  движения.  

3.3.1  Включить прибор, установить высоту равно-

  мерного движения груза h и записать расстояние между

  средним и нижним кронштейнами в таблицу 3.1.

3.3.2 Используя предложенный преподавателем

  перегрузок, измерить время t равномерного движения

  грузов для пяти различных расстояний h, оставляя  не-

  изменным расстояние S между верхним и нижним

  кронштейнами. Полученные данные занести в таблицу 3.1.

          Рисунок 3.1

          

         Таблица 3.1

h, м

t, c

V, M/C

Упражнение 2. Проверка формулы равноускоренного движения.

3.3.3 Перемещая подвижные кронштейны, установить выбранные расстояния  равноускоренного  S  и равномерного h движения груза и записать их в таблицу 2.2

Таблица 3.2

S, М

h, м

t, c

a, м/с2

 Упражнение 3. Проверка второго закона Ньютона.

          3.3.4 Установить   некоторое   расстояние   h   между   средним   и   нижним  кронштейнами.

         3.3.5 Положить на правый груз три перегрузка (используя грузы малого диаметра, которые кольцом не снимаются) и записать их общую массу в таблицу 3.

---

Смотрите также файлы

• Отчет лабораторной работы 14 Тема Настройка браузера Microsoft Edge.docx

• ОТстік азастан мемлекеттік педогогикалы университеті таырыбы Сурат кофеханасы.docx

• Фонд оценочных средств для проведения промежуточной аттестации обучающихся по дисциплине Системы тягового электроснабжения.pdf

• Лабораторная работа Изучение явления внешнего фотоэффекта. Цель работы Изучить работу фотоэлемента, законы фотоэффекта.docx

• аралан мселелер.docx