Файл: Методические указания к выполнению лабораторных работ для студентов всех форм обучения всех специальностей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 144
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
э – время n полных колебаний (см. п.п. 3-5). 7.3.7 Убрать образец и произвести измерение времени tр полных n колебаний пустой рамки. Каждый опыт повторить не менее трех раз.
Таблица 7.1
7.4 Обработка результатов
7.4.1 Вычислить периоды T0, Tэ и Тр по формуле Т= t/n, и их средние значения <T0>,< Tэ> и <Тр>;
7.4.2 Вычислить момент инерции I0 исследуемого образца по формуле (8), подставляя в нее средние значения соответствующих периодов. Примечание: значение момента инерции эталонного образца приведено на справочном стенде в лаборатории "Механика и молекулярная физика".
7.5 Контрольные вопросы 7.5.1Что лежит в основе используемой в данной работе методики экспериментального определения момента инерции тел? 7.5.2 Каковы основные источники погрешностей в данном эксперименте?
8 Лабораторная работа ММФ -7. Определение скорости полета снаряда на баллистическом крутильном маятнике
Цель работы: овладение методом определения скорости тела, основанном на применении законов сохранения. Задачи:
- изучить возможности применения законов сохранения момента импульса и энергии;
- определить скорость полета снаряда.
8.1 Методика экспериментаБаллистический крутильный маятник представляет собой стержень, подвешенный на вертикально натянутой стальной проволоке и способный совершать колебательное движение в горизонтальной плоскости. На концах стержня закреплены две мишени, заполненные пластилином. Также на стержне расположены два одинаковых цилиндрических груза, которые можно перемещать и закреплять в выбранном положении (рисунок 8.1). При попадании в мишень горизонтально летящего со скоростью v снаряда маятник отклоняется от положения равновесия, поворачиваясь вокруг своей оси с начальной угловой скоростью
0. Согласно закону сохранения момента импульса
здесь m0 – масса снаряда;
r – плечо его импульса, равное расстоянию от оси до того места на мишени, где застрял снаряд (при условии, что его скорость перпендикулярна оси стержня);
I – момент инерции маятника. При повороте маятника проволока, на которой он подвешен, закручивается. В ней возникают упругие силы, момент которых пропорционален углу поворота маятника,
где k – коэффициент, зависящий от длины, радиуса и материала проволоки. Под действием момента упругих сил маятник совершает свободные крутильные колебания с периодом, равным
Кинетическая энергия, полученная маятником при ударе, переходит в потенциальную энергию упругой деформации проволоки. Если пренебречь потерей энергии при движении маятника (вследствие сопротивления воздуха), то можно записать закон сохранения механической энергии в следующем виде
где m – максимальный угол, на который повернется маятник после удара.
Из соотношений (1) и (3) получим
В (5) учтено, что m0r2<< I, т.е. моментом инерции снаряда можно пренебречь.
Для того, чтобы исключить из расчетной формулы неизвестные нам величины k и I, необходимо произвести измерения периодов
Т и Т1 колебаний маятника при двух различных положениях грузов на расстояниях соответственно R и R1 от оси вращения. Тогда расчетная формула приобретает следующий вид
где m – масса груза. Таким образом, методика определения скорости полета снаряда с помощью баллистического крутильного маятника основана на применении законов сохранения момента импульса и механической энергии. Суть ее заключается в проведении двух опытов, в одном из которых определяют угол m отклонения маятника после удара и период Т его свободных колебаний, грузы при этом расположены симметрично, на расстояние R от оси. Во втором опыте грузы располагают на другом расстоянии, которое мы обозначили R1, и вновь определяют период колебаний маятника – Т1 в нашем обозначении.
8.2 Экспериментальная установкаПрибор "баллистический крутильный маятник FRM-09" состоит из описанного выше маятника, стреляющего устройства, фотоэлектрического датчика и соединенных с ним электронного миллисекундомера и счетчика колебаний. Также имеется прозрачный экран с нанесенной на него угловой шкалой. На лицевой панели секундомера расположены клавишные выключатели СЕТЬ, СБРОС, СТОП и цифровые индикаторы, высвечивающие показания миллисекундомера и счетчика колебаний.
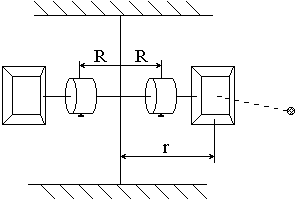
Рисунок 8.1
8.3 Проведение эксперимента8.3.1 Выравнить прибор. 8.3.2 Максимально приблизить грузы друг к другу, т.е. сдвинуть их к оси, и измерить расстояние R до центра каждого груза. 8.3.3 Установить маятник в нулевом положении, когда черта на торце мишени располагается напротив нулевого деления угловой шкалы. Включить прибор в сеть. 8.3.4 Заложить снаряд в стреляющее устройство и произвести выстрел. 8.3.5 Определить по шкале угол
m максимального поворота маятника после удара снаряда о мишень и выразить его в радианах. 8.3.6 Определить t – время n = 710 полных колебаний маятника. 8.3.7 Измерить r – расстояние от оси до того места на мишени, где застрял снаряд. 8.3.8 Максимально раздвинуть грузы и определить их расстояние R1 до оси.
8.3.9 Повернуть маятник на угол, равный m, нажать клавишу СБРОС, затем отпустить маятник и определить t1 – время полных n1 колебаний маятника.
8.3.10 Каждый опыт повторить не менее трех раз. Результаты измерений занести в таблицу 8.1
Таблица 8.1
8.4 Обработка результатов8.4.1 Вычислить для каждого опыта периоды колебаний по формулам: Т = t/n и T1=t1/n1; затем вычислить их средние значения <T> и <T1>.
8.4.2 Для каждого из полученных в опыте значений m вычислить скорость v, подставляя в расчетную формулу (5) средние значения периодов <T> и <T1>.
8.4.3 Вычислить среднее значение скорости. Примечание. Массы грузов m и снаряда m0 указаны на справочном стенде в лаборатории "Механика и молекулярная физика".
8.5 Контрольные вопросы8.5.1 При каких условиях сохраняется момент импульса системы относительно некоторой оси Z? 8.5.2 При каких условиях сохраняется механическая энергия системы? 8.5.3 Сохраняется ли механическая энергия системы: баллистический крутильный маятник – снаряд, при условии попадания снаряда в мишень? 8.5.4 При каких условиях расстояние от места попадания снаряда в мишень до оси можно считать равным плечу импульса летящего снаряда относительно оси маятника? 8.5.5 Какие обстоятельства и факты определяют точность эксперимента на данной установке?
9 Лабораторная работа ММФ – 8. Изучение динамики вращательного движения на маятнике Обербека
Цель работы: проверка закона (уравнения) динамики вращательного движения твердого тела относительно неподвижной оси. Задачи:
- определить значения момента М внешней силы, углового ускорения ε вращающегося тела и его момента инерции I;
- проверить соотношения, вытекающие из закона динамики вращательного движения в двух случаях: а) I = const, б) M = const.
9.1 Методика экспериментаУравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет вид
здесь I – момент инерции тела относительно оси вращения Z;
z = ddt – проекция углового ускорения на ось Z;
Mz – суммарный момент внешних сил относительно оси Z.
Из уравнения (1) следует, что, если под действием момента силы М1 тело вращается относительно неподвижной оси с ускорением 1, а под действием момента силы М2 – с ускорением 2, то, при неизменной величине момента инерции тела (I = const) относительно данной оси, справедливо равенство отношений
Еще одно следствие из уравнения (1) заключается в том, что отношение ускорений 1 и 2, приобретаемых телами с моментами инерции I1 и I2 под действием одного и того же момента силы (М = const), обратно отношению их моментов инерции
Проверка соотношений (2) и(3) осуществляется на маятнике Обербека. Маятник Обербека представляет собой маховик в виде крестовины (четырех взаимноперпендикулярных стержней, скрепленных со шкивом), способный вращаться вокруг горизонтальной оси (рисунок 9.1). На этой оси имеется двухступенчатый диск, на котором закреплена нить. К другому концу нити подвешен груз. При наматывании нити на диск груз поднимается на некоторую высоту h. При опускании груза нить, разматываясь с диска, приводит во вращение маховик. На груз действуют сила тяжести и сила натяжения нити, направленные в противоположные стороны. Под действием результирующей этих сил груз движется, согласно второму закону Ньютона, с постоянным ускорением
При этом ускорение, пройденный путь и время движения связаны формулой
Из уравнения (4) с учетом (5) получим для натяжения нити:
Натяжение нити создает вращающий момент
который сообщает маховику угловое ускорение. Последнее связано с тангенциальным ускорением точек обода диска и его радиусом соотношением
Поскольку нить нерастяжима и не проскальзывает, то тангенциальное ускорение указанных точек диска равно ускорению груза:
Следовательно
При выводе расчетной формулы для момента инерции маятника Обербека воспользуемся законом сохранения энергии
Учтем, что при равноускоренном движении без начальной скорости
и получим искомую формулу
Таким образом, для проверки соотношений (2) и (3) необходимо измерить время падения груза с заданной высоты, радиус диска и массу груза, затем вычислить по формулам (7), (8) и (12) соответствующие величины.
9.2 Экспериментальная установкаУстановка состоит из крестовины (рисунок 9.1), двухступенчатого диска, тормозного электромагнита и универсального электронного миллисекундомера, соединенного с двумя фотоэлектрическими датчиками. Имеется также малоинерционный блок, через который перекинута нить. Один конец нити закреплен на диске, на другом ее конце подвешен груз (имеется набор грузов различной массы). В комплект входят четыре одинаковых цилиндрических груза, которые можно надеть на стержни и перемещать вдоль них, изменяя таким образом момент инерции маятника.
Тормозной электромагнит при подключении к нему напряжения питания способен удерживать маховик вместе с грузами в состояние покоя. При прерывании светового луча падающим грузом верхний ф э датчик вырабатывает электроимпульс начала отсчета времени, а второй ф э датчик – конца измерения времени и включения тормозного электромагнита. На лицевой панели секундомера расположены клавишные выключатели СЕТЬ, ПУСК, СБРОС и цифровые индикаторы, высвечивающие показания секундомера.
Рисунок 9.1
9.3 Выполнение эксперимента Задание 1: проверка соотношения (2).
9.3.1 Выравнить прибор и включить его в сеть.
9.3.2 Подвесить к нити груз массой m1.
9.3.3 Вращением крестовины наматывая нить на одну из ступеней диска, поднять груз на высоту h. При этом нижний край груза установить на уровне черты, которая нанесена на корпусе верхнего ф э датчика.
9.3.4 Отжать клавишу ПУСК, блокируя электромагнит.
9.3.5 Нажать клавишу СБРОС, затем клавишу ПУСК, что вызовет движение маятника и включение секундомера.
9.3.6 После остановки маятника считать показания секундомера и занести в таблицу 9.1.
9.3.7 По миллиметровой шкале, нанесенной на колонне, определить высоту h – длину пройденного грузом пути и занести в таблицу 9.1.
Таблица 9.1
9.3.8 Нажать клавишу СБРОС и повторить опыт (п.п.3-6) не менее трех раз.
9.3.9 Добавить еще один или два груза и выполнить измерения времени (п.п.3-8) с грузом массы m2.
9.3.10 С помощью штангенциркуля измерить диаметр используемой ступени диска и найти его радиус r.
Задание 2: проверка соотношения (3).
9.3.11 Подвесить к нити не менее двух грузов общей массой m, значение которой занести в таблицу 9.2.
9.3.12 Надеть цилиндрические грузы на стержни и расположить их на некотором расстоянии (2-5см) от концов стержней. При этом необходимо добиться безразличного равновесия маховика (когда нить не натянута).
9.3.13 Измерить не менее трех раз время t падения груза с высоты h (п.п.3-8). 9.3.14 Сдвинуть грузы на стержнях ближе к шкиву. При новом расположении грузов маховик должен находиться в состоянии равновесия (см. п.12).
9.3.15 Измерить не менее трех раз время падения груза с высоты h.
Все полученные данные занести в таблицу 9.2.
Таблица 9.2
9.4 Обработка результатов 9.4.1 Используя результаты измерений, занесенные в таблицу 9.1, вычислить:
а) среднее значение1> и 2> времен движения грузов m1 и m2 соответственно;
б) значения 1и 2, М1 и М2 подставляя в формулы (7) и (8) средние значения1> и 2> соответственно;
в) отношения 12 и М1/ М2.
9.4.2 Проверить справедливость соотношения (2).
9.4.3 Используя результаты измерений, занесенные в таблицу 9.2, вычислить:
а) среднее значение1> и 2> времен для двух положений грузов на стержнях;
б) значения 1 и 2, I1 и I2 по формулам (8) и (10), подставляя в них средние значения1> и 2> соответственно;
в) отношения 12 и I2/I1. 9.4.4 Проверить справедливость соотношения (3).
9.5 Контрольные вопросы9.5.1 Увеличивается или уменьшается угловое ускорение маховика, если к грузу, подвешенному на нити, добавить второй груз?
9.5.2 При каком расположении грузов на стержнях момент инерции маховика наибольший? наименьший?
9.5.3 Как от расположения грузов на стержнях зависит угловое ускорение маховика?
9.5.4 Зависит ли от расположения грузов на стержнях ускорение подвешенного к нити груза?
9.5.5 Какие факторы не учтены при выводе расчетных формул в описании методики эксперимента?
9.5.6 Каковы основные источники погрешностей в данном эксперименте?
10 Лабораторная работа ММФ – 9. Изучение гироскопического эффекта
Цель работы: изучение законов динамики вращательного движения твердых тел вокруг их свободных осей на примере вынужденной прецессии гироскопа. Задачи:
- определить значение момента импульса гироскопа;
- определить значение главного момента инерции гироскопа.
10.1 Методика эксперимента Гироскопом называется массивное аксиально симметричное твердое тело, быстро вращающееся вокруг своей оси симметрии. Благодаря специальному карданному подвесу ось гироскопа может свободно поворачиваться в любом направлении. Все явления, обусловленные быстрым вращением гироскопа, называются гироскопическими. Одно из них заключается в том, что приведенный в быстрое вращение вокруг своей оси гироскоп сохраняет это направление оси устойчивого вращения. Это обстоятельство делает гироскоп важнейшим навигационным инструментом при полете ракет и главным элементом автопилота. Наиболее интересным видом движения гироскопа является вынужденная прецессия. Гироскоп обычно закреплен в точке "О" центра масс и при этом может свободно вращаться не только вокруг своей оси фигуры OZ, но также и вокруг вертикальной и горизонтальной осей OY и OX (рисунок 10.1). Приложим в какой – либо точке А оси фигуры гироскопа постоянную силу
F, например, закрепим небольшой груз массы m. В этом случае F = mg. Когда маховик гироскопа не вращается, то наблюдается привычное явление – под действием груза ось гироскопа наклоняется. Однако, если предварительно маховик был приведен в быстрое вращение, то в этом случае ось фигуры гироскопа не опускается, а начинает медленно вращаться с постоянной скоростью вокруг оси OY. Такое вращение называется вынужденной прецессией. К гироскопу применимо уравнение моментов
где L = момент импульса направлен вдоль главной оси гироскопа (ось OZ на рисунке 10.1);
М – момент внешней силы относительно точки "О", который в данном случае перпендикулярен вектору L и поэтому изменяет не величину момента импульса, а его направление. В итоге, ось гироскопа будет поворачиваться вокруг вертикальной оси. Угловая скорость прецессии при этом определяется моментом М приложенной силы и моментом Lимпульса гироскопа
здесь I момент инерции гироскопа относительно его фигуры (главный момент инерции). Момент приложенной силы равен по модулю
где l плечо силы относительно т. "0". Гироскоп прибора FPM 10 устроен так, что при некотором положении груза центр масс системы совпадает с точкой "О" подвеса и гироскоп находится в равновесии. Прецессия возникает, если груз сместить на некоторое расстояние
Таблица 7.1
| № | n | t0, c | tэ, c | tp, c | T0, c | Tэ, c | Тр, с | I0, кг м2 |
7.4 Обработка результатов
7.4.1 Вычислить периоды T0, Tэ и Тр по формуле Т= t/n, и их средние значения <T0>,< Tэ> и <Тр>;
7.4.2 Вычислить момент инерции I0 исследуемого образца по формуле (8), подставляя в нее средние значения соответствующих периодов. Примечание: значение момента инерции эталонного образца приведено на справочном стенде в лаборатории "Механика и молекулярная физика".
7.5 Контрольные вопросы 7.5.1Что лежит в основе используемой в данной работе методики экспериментального определения момента инерции тел? 7.5.2 Каковы основные источники погрешностей в данном эксперименте?
8 Лабораторная работа ММФ -7. Определение скорости полета снаряда на баллистическом крутильном маятнике
Цель работы: овладение методом определения скорости тела, основанном на применении законов сохранения. Задачи:
- изучить возможности применения законов сохранения момента импульса и энергии;
- определить скорость полета снаряда.
8.1 Методика экспериментаБаллистический крутильный маятник представляет собой стержень, подвешенный на вертикально натянутой стальной проволоке и способный совершать колебательное движение в горизонтальной плоскости. На концах стержня закреплены две мишени, заполненные пластилином. Также на стержне расположены два одинаковых цилиндрических груза, которые можно перемещать и закреплять в выбранном положении (рисунок 8.1). При попадании в мишень горизонтально летящего со скоростью v снаряда маятник отклоняется от положения равновесия, поворачиваясь вокруг своей оси с начальной угловой скоростью
0. Согласно закону сохранения момента импульса
| | m0vr = (I + m0r2) 0 | (1) |
здесь m0 – масса снаряда;
r – плечо его импульса, равное расстоянию от оси до того места на мишени, где застрял снаряд (при условии, что его скорость перпендикулярна оси стержня);
I – момент инерции маятника. При повороте маятника проволока, на которой он подвешен, закручивается. В ней возникают упругие силы, момент которых пропорционален углу поворота маятника,
| | M = - k | (2) |
где k – коэффициент, зависящий от длины, радиуса и материала проволоки. Под действием момента упругих сил маятник совершает свободные крутильные колебания с периодом, равным
| |  | (3) |
Кинетическая энергия, полученная маятником при ударе, переходит в потенциальную энергию упругой деформации проволоки. Если пренебречь потерей энергии при движении маятника (вследствие сопротивления воздуха), то можно записать закон сохранения механической энергии в следующем виде
| |  | (4) |
где m – максимальный угол, на который повернется маятник после удара.
Из соотношений (1) и (3) получим
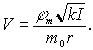| |  | (5) |
В (5) учтено, что m0r2<< I, т.е. моментом инерции снаряда можно пренебречь.
Для того, чтобы исключить из расчетной формулы неизвестные нам величины k и I, необходимо произвести измерения периодов
Т и Т1 колебаний маятника при двух различных положениях грузов на расстояниях соответственно R и R1 от оси вращения. Тогда расчетная формула приобретает следующий вид
| |  | (6) |
где m – масса груза. Таким образом, методика определения скорости полета снаряда с помощью баллистического крутильного маятника основана на применении законов сохранения момента импульса и механической энергии. Суть ее заключается в проведении двух опытов, в одном из которых определяют угол m отклонения маятника после удара и период Т его свободных колебаний, грузы при этом расположены симметрично, на расстояние R от оси. Во втором опыте грузы располагают на другом расстоянии, которое мы обозначили R1, и вновь определяют период колебаний маятника – Т1 в нашем обозначении.
8.2 Экспериментальная установкаПрибор "баллистический крутильный маятник FRM-09" состоит из описанного выше маятника, стреляющего устройства, фотоэлектрического датчика и соединенных с ним электронного миллисекундомера и счетчика колебаний. Также имеется прозрачный экран с нанесенной на него угловой шкалой. На лицевой панели секундомера расположены клавишные выключатели СЕТЬ, СБРОС, СТОП и цифровые индикаторы, высвечивающие показания миллисекундомера и счетчика колебаний.
Рисунок 8.1
8.3 Проведение эксперимента8.3.1 Выравнить прибор. 8.3.2 Максимально приблизить грузы друг к другу, т.е. сдвинуть их к оси, и измерить расстояние R до центра каждого груза. 8.3.3 Установить маятник в нулевом положении, когда черта на торце мишени располагается напротив нулевого деления угловой шкалы. Включить прибор в сеть. 8.3.4 Заложить снаряд в стреляющее устройство и произвести выстрел. 8.3.5 Определить по шкале угол
m максимального поворота маятника после удара снаряда о мишень и выразить его в радианах. 8.3.6 Определить t – время n = 710 полных колебаний маятника. 8.3.7 Измерить r – расстояние от оси до того места на мишени, где застрял снаряд. 8.3.8 Максимально раздвинуть грузы и определить их расстояние R1 до оси.
8.3.9 Повернуть маятник на угол, равный m, нажать клавишу СБРОС, затем отпустить маятник и определить t1 – время полных n1 колебаний маятника.
8.3.10 Каждый опыт повторить не менее трех раз. Результаты измерений занести в таблицу 8.1
Таблица 8.1
| № | m, рад. | R, м | t, c | n | <T>, c | t1, c | n1 | <T1>, c | R1, м | r, м | v, м с | <v>, м с |
| | | | | | | | | | | | | |
8.4 Обработка результатов8.4.1 Вычислить для каждого опыта периоды колебаний по формулам: Т = t/n и T1=t1/n1; затем вычислить их средние значения <T> и <T1>.
8.4.2 Для каждого из полученных в опыте значений m вычислить скорость v, подставляя в расчетную формулу (5) средние значения периодов <T> и <T1>.
8.4.3 Вычислить среднее значение скорости
8.5 Контрольные вопросы8.5.1 При каких условиях сохраняется момент импульса системы относительно некоторой оси Z? 8.5.2 При каких условиях сохраняется механическая энергия системы? 8.5.3 Сохраняется ли механическая энергия системы: баллистический крутильный маятник – снаряд, при условии попадания снаряда в мишень? 8.5.4 При каких условиях расстояние от места попадания снаряда в мишень до оси можно считать равным плечу импульса летящего снаряда относительно оси маятника? 8.5.5 Какие обстоятельства и факты определяют точность эксперимента на данной установке?
9 Лабораторная работа ММФ – 8. Изучение динамики вращательного движения на маятнике Обербека
Цель работы: проверка закона (уравнения) динамики вращательного движения твердого тела относительно неподвижной оси. Задачи:
- определить значения момента М внешней силы, углового ускорения ε вращающегося тела и его момента инерции I;
- проверить соотношения, вытекающие из закона динамики вращательного движения в двух случаях: а) I = const, б) M = const.
9.1 Методика экспериментаУравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет вид
| | I·z = Mz | (1) |
здесь I – момент инерции тела относительно оси вращения Z;
z = ddt – проекция углового ускорения на ось Z;
Mz – суммарный момент внешних сил относительно оси Z.
Из уравнения (1) следует, что, если под действием момента силы М1 тело вращается относительно неподвижной оси с ускорением 1, а под действием момента силы М2 – с ускорением 2, то, при неизменной величине момента инерции тела (I = const) относительно данной оси, справедливо равенство отношений
| | 1 2 = М1/ М2. | (2) |
Еще одно следствие из уравнения (1) заключается в том, что отношение ускорений 1 и 2, приобретаемых телами с моментами инерции I1 и I2 под действием одного и того же момента силы (М = const), обратно отношению их моментов инерции
| | 1 2 = I2/ I1. | (3) |
Проверка соотношений (2) и(3) осуществляется на маятнике Обербека. Маятник Обербека представляет собой маховик в виде крестовины (четырех взаимноперпендикулярных стержней, скрепленных со шкивом), способный вращаться вокруг горизонтальной оси (рисунок 9.1). На этой оси имеется двухступенчатый диск, на котором закреплена нить. К другому концу нити подвешен груз. При наматывании нити на диск груз поднимается на некоторую высоту h. При опускании груза нить, разматываясь с диска, приводит во вращение маховик. На груз действуют сила тяжести и сила натяжения нити, направленные в противоположные стороны. Под действием результирующей этих сил груз движется, согласно второму закону Ньютона, с постоянным ускорением
| | ma = mg – T . | (4) |
При этом ускорение, пройденный путь и время движения связаны формулой
| | a = 2h/t2 . | (5) |
Из уравнения (4) с учетом (5) получим для натяжения нити:
| |  | (6) |
Натяжение нити создает вращающий момент
| |  | (7) |
который сообщает маховику угловое ускорение. Последнее связано с тангенциальным ускорением точек обода диска и его радиусом соотношением
| | = aτ / r. | |
Поскольку нить нерастяжима и не проскальзывает, то тангенциальное ускорение указанных точек диска равно ускорению груза:
| | aτ = а. | |
Следовательно
| |  | (8) |
При выводе расчетной формулы для момента инерции маятника Обербека воспользуемся законом сохранения энергии
| |  | (9) |
Учтем, что при равноускоренном движении без начальной скорости
| | v = at = 2h/t , t = 2h/rt, | (10) (11) |
и получим искомую формулу
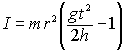| |  . | (12) |
Таким образом, для проверки соотношений (2) и (3) необходимо измерить время падения груза с заданной высоты, радиус диска и массу груза, затем вычислить по формулам (7), (8) и (12) соответствующие величины.
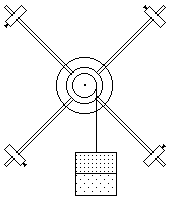
9.2 Экспериментальная установкаУстановка состоит из крестовины (рисунок 9.1), двухступенчатого диска, тормозного электромагнита и универсального электронного миллисекундомера, соединенного с двумя фотоэлектрическими датчиками. Имеется также малоинерционный блок, через который перекинута нить. Один конец нити закреплен на диске, на другом ее конце подвешен груз (имеется набор грузов различной массы). В комплект входят четыре одинаковых цилиндрических груза, которые можно надеть на стержни и перемещать вдоль них, изменяя таким образом момент инерции маятника.
Тормозной электромагнит при подключении к нему напряжения питания способен удерживать маховик вместе с грузами в состояние покоя. При прерывании светового луча падающим грузом верхний ф э датчик вырабатывает электроимпульс начала отсчета времени, а второй ф э датчик – конца измерения времени и включения тормозного электромагнита. На лицевой панели секундомера расположены клавишные выключатели СЕТЬ, ПУСК, СБРОС и цифровые индикаторы, высвечивающие показания секундомера.Рисунок 9.1
9.3 Выполнение эксперимента Задание 1: проверка соотношения (2).
9.3.1 Выравнить прибор и включить его в сеть.
9.3.2 Подвесить к нити груз массой m1.
9.3.3 Вращением крестовины наматывая нить на одну из ступеней диска, поднять груз на высоту h. При этом нижний край груза установить на уровне черты, которая нанесена на корпусе верхнего ф э датчика.
9.3.4 Отжать клавишу ПУСК, блокируя электромагнит.
9.3.5 Нажать клавишу СБРОС, затем клавишу ПУСК, что вызовет движение маятника и включение секундомера.
9.3.6 После остановки маятника считать показания секундомера и занести в таблицу 9.1.
9.3.7 По миллиметровой шкале, нанесенной на колонне, определить высоту h – длину пройденного грузом пути и занести в таблицу 9.1.
Таблица 9.1
| № | h, м | r, м | m, кг | t, c | <t>, c | М, Н·м | , с-2 | 1 2 | М1М2 |
9.3.8 Нажать клавишу СБРОС и повторить опыт (п.п.3-6) не менее трех раз.
9.3.9 Добавить еще один или два груза и выполнить измерения времени (п.п.3-8) с грузом массы m2.
9.3.10 С помощью штангенциркуля измерить диаметр используемой ступени диска и найти его радиус r.
Задание 2: проверка соотношения (3).
9.3.11 Подвесить к нити не менее двух грузов общей массой m, значение которой занести в таблицу 9.2.
9.3.12 Надеть цилиндрические грузы на стержни и расположить их на некотором расстоянии (2-5см) от концов стержней. При этом необходимо добиться безразличного равновесия маховика (когда нить не натянута).
9.3.13 Измерить не менее трех раз время t падения груза с высоты h (п.п.3-8). 9.3.14 Сдвинуть грузы на стержнях ближе к шкиву. При новом расположении грузов маховик должен находиться в состоянии равновесия (см. п.12).
9.3.15 Измерить не менее трех раз время падения груза с высоты h.
Все полученные данные занести в таблицу 9.2.
Таблица 9.2
| № | h, м | r, м | m, кг | Положение грузов на стержнях | t, c | <t>, c | , с-2 | I, кг·м2 | 1/ 2 | I2I1 |
9.4 Обработка результатов 9.4.1 Используя результаты измерений, занесенные в таблицу 9.1, вычислить:
а) среднее значение
б) значения 1и 2, М1 и М2 подставляя в формулы (7) и (8) средние значения
в) отношения 12 и М1/ М2.
9.4.2 Проверить справедливость соотношения (2).
9.4.3 Используя результаты измерений, занесенные в таблицу 9.2, вычислить:
а) среднее значение
б) значения 1 и 2, I1 и I2 по формулам (8) и (10), подставляя в них средние значения
в) отношения 12 и I2/I1. 9.4.4 Проверить справедливость соотношения (3).
9.5 Контрольные вопросы9.5.1 Увеличивается или уменьшается угловое ускорение маховика, если к грузу, подвешенному на нити, добавить второй груз?
9.5.2 При каком расположении грузов на стержнях момент инерции маховика наибольший? наименьший?
9.5.3 Как от расположения грузов на стержнях зависит угловое ускорение маховика?
9.5.4 Зависит ли от расположения грузов на стержнях ускорение подвешенного к нити груза?
9.5.5 Какие факторы не учтены при выводе расчетных формул в описании методики эксперимента?
9.5.6 Каковы основные источники погрешностей в данном эксперименте?
10 Лабораторная работа ММФ – 9. Изучение гироскопического эффекта
Цель работы: изучение законов динамики вращательного движения твердых тел вокруг их свободных осей на примере вынужденной прецессии гироскопа. Задачи:
- определить значение момента импульса гироскопа;
- определить значение главного момента инерции гироскопа.
10.1 Методика эксперимента Гироскопом называется массивное аксиально симметричное твердое тело, быстро вращающееся вокруг своей оси симметрии. Благодаря специальному карданному подвесу ось гироскопа может свободно поворачиваться в любом направлении. Все явления, обусловленные быстрым вращением гироскопа, называются гироскопическими. Одно из них заключается в том, что приведенный в быстрое вращение вокруг своей оси гироскоп сохраняет это направление оси устойчивого вращения. Это обстоятельство делает гироскоп важнейшим навигационным инструментом при полете ракет и главным элементом автопилота. Наиболее интересным видом движения гироскопа является вынужденная прецессия. Гироскоп обычно закреплен в точке "О" центра масс и при этом может свободно вращаться не только вокруг своей оси фигуры OZ, но также и вокруг вертикальной и горизонтальной осей OY и OX (рисунок 10.1). Приложим в какой – либо точке А оси фигуры гироскопа постоянную силу
F, например, закрепим небольшой груз массы m. В этом случае F = mg. Когда маховик гироскопа не вращается, то наблюдается привычное явление – под действием груза ось гироскопа наклоняется. Однако, если предварительно маховик был приведен в быстрое вращение, то в этом случае ось фигуры гироскопа не опускается, а начинает медленно вращаться с постоянной скоростью вокруг оси OY. Такое вращение называется вынужденной прецессией. К гироскопу применимо уравнение моментов
| | dL/dt = M | (1) |
где L = момент импульса направлен вдоль главной оси гироскопа (ось OZ на рисунке 10.1);
М – момент внешней силы относительно точки "О", который в данном случае перпендикулярен вектору L и поэтому изменяет не величину момента импульса, а его направление. В итоге, ось гироскопа будет поворачиваться вокруг вертикальной оси. Угловая скорость прецессии при этом определяется моментом М приложенной силы и моментом Lимпульса гироскопа
| |  | (2) |
| или | | |
| |  | (2') |
здесь I момент инерции гироскопа относительно его фигуры (главный момент инерции). Момент приложенной силы равен по модулю
| | M = lF = lmg | (3) |
где l плечо силы относительно т. "0". Гироскоп прибора FPM 10 устроен так, что при некотором положении груза центр масс системы совпадает с точкой "О" подвеса и гироскоп находится в равновесии. Прецессия возникает, если груз сместить на некоторое расстояние