Файл: Методические указания к выполнению лабораторных работ для студентов всех форм обучения всех специальностей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- сравнить полученные значения.
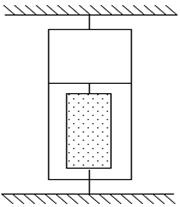
6.1 Методика экспериментаМаятник Максвелла представляет собой диск, насаженный на легкую трубку и подвешенный на двух нитях (рисунок 6.1). Если, намотав нити симметрично на трубку, поднять диск на высоту h, а затем отпустить без толчка, то он начнет опускаться, одновременно вращаясь вокруг горизонтальной оси. При этом траектории всех точек диска лежат в параллельных плоскостях. Такое движение твердого тела называется плоским. Его можно рассматривать как поступательное движение тела, происходящее со скоростью центра масс, и одновременное вращение вокруг горизонтальной оси, проходящей через этот центр.
Уравнения движения центра масс и вращения маятника относительно указанной оси в этом случае имеют вид
| | ma = mg – 2T, I· = 2T·r | (1) (2) |
где m – масса маятника;
I – его момент инерции;
а – ускорение центра масс;
– угловое ускорение маятника;
Т – натяжение нити;
r – радиус трубки (плечо силы натяжения).
Учитывая, что ускорения в данном случае связаны соотношением а = · r,
получим из (1) и (2)
| | 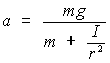 | (3) |
Из последнего выражения следует, что центр масс маятника движется с постоянным ускорением, которое зависит от момента инерции. Это обстоятельство и лежит в основе рассматриваемой методики. Из соотношения (3) с учетом формулы пути равноускоренного движения h = at2/2, получим расчетную формулу
| | 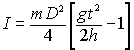 | (4) |
где D = D0 + d. Таким образом, для определения момента инерции маятника Максвелла необходимо измерить время
t его падения с заданной высоты h, определить его массу m, диаметр трубки D0 и толщину d нити.
6.2 Экспериментальная установкаПрибор "Маятник Максвелла FPM-03" состоит из собственно маятника (описанного выше), электромагнита, двух фотоэлектрических датчиков и соединенного с ними электронного миллисекундомера. На диск маятника накладывается одно из имеющихся в комплекте сменных колец, что позволяет изменять момент инерции маятника и его массу. Электромагнит при протекании электрического тока по его обмотке удерживает маятник в верхнем положении. Длину подвески маятника (высоту h) изменяют по миллиметровой шкале, нанесенной на вертикальной колонне. На лицевой панели миллисекундомера расположены клавишные выключатели СЕТЬ, ПУСК, СБРОС и цифровые индикаторы, которые высвечивают показания миллисекундомера.
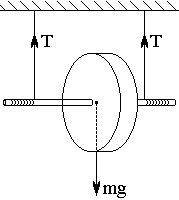
6.3 Проведение эксперимента 6.3.1 Выравнить прибор и включить его в сеть. 6.3.2 Отрегулировать длину нити так, чтобы в нижнем положении край стального кольца перекрывал световой пучок ф/э датчика и чтобы ось маятника была горизонтальной.
Рисунок 6.1
6.3.3 Равномерно в один слой наматывая нити на трубку, поднять маятник в верхнее положение и зафиксировать с помощью электромагнита. Клавиша ПУСК при этом должна быть отжата.
6.3.4 Нажать последовательно клавиши СБРОС и ПУСК, что вызовет освобождение маятника и запуск миллисекундомера.
6.3.5 Считать показания миллисекундомера. Повторить опыт не менее 5 раз. Результаты измерений занести в таблицу 6.1.
6.3.6 Измерить штангенциркулем внешние диаметры трубки D0, диска DД и кольца DК; определить толщину нити d.
Таблица 6.1
| № | h, м | m, кг | t, c | I, кг· м2 | <I>, кг· м2 | D0, м | DД, м | DК, м | Iтеор, кг· м2 |
6.4 Обработка результатов
6.4.1 Выписать значения масс трубки m0, диска mд, и кольца mк, выгравированные на соответствующих деталях, и вычислить массу m маятника.
6.4.2 Вычислить по формуле (4) значения момента инерции I для каждого из полученных в опыте значений времени t.
6.4.3 Вычислить среднее арифметическое значение <I> и оценить его случайную погрешность I для доверительной вероятности = 0,95.
6.4.4 Вычислить теоретическое значение момента инерции маятника по формуле
| | Iтеор=[m0D02+ mд(Dд2 + D02) + mк(Dк2 + Dд2)]/8, | (5) |
и сравнить его со значением <I>.
6.5 Контрольные вопросы 6.5.1 От чего зависит время падения маятника Максвелла с данной высоты h?
6.5.2 Как движется центр масс маятника? От чего зависит его ускорение?
6.5.3 Чему равна механическая энергия маятника в верхнем положении? При прохождении нижнего положения? Каково отношение этих значений?
6.5.4 Укажите источники погрешностей в опыте.
7 Лабораторная работа ММФ – 6. Определение момента инерции твердых тел с помощью крутильных колебаний
Цель работы: овладение методом определения момента инерции тела, который основан на применении закона динамики вращательного движения тела.
Задачи:
- определить периоды крутильных колебаний маятника с закрепленными на нем телами; - вычислить момент инерции тела с использованием полученных в опыте значений периодов колебаний.
7.1 Методика экспериментаКрутильный маятник представляет собой тело, закрепленное на вертикально натянутой стальной проволоке. При повороте маятника вокруг оси, совпадающей с осью проволоки, в ней возникают упругие силы, момент которых пропорционален углу поворота
| | M = -k | (1) |
где k – коэффициент, зависящий от радиуса и длины проволоки, а также – от упругих свойств материала, из которого она изготовлена.
Уравнение динамики вращательного движения в данном случае имеет вид
| | I = -k . | (2) |
С учетом определения углового ускорения и после небольших преобразований запишем
| | 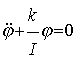 | (3) |
Последнее уравнение представляет собой дифференциальное уравнение свободных крутильных колебаний, период которых равен
| | | (4) |
Именно зависимость периода крутильных колебаний от момента инерции тела, подвешенного на проволоке, и лежит в основе предлагаемой методики. Обычно на проволоке подвешивают рамку, конструкция которой позволяет закреплять в ней образцы, значительно отличающиеся по своим размерам. Эта рамка обладает моментом инерции Iр. Если в ней закрепить исследуемый образец с моментом инерции I0, то период такого маятника равен
| | To=2π | (5) |
Чтобы исключить из расчетной формулы неизвестные нам величины Iр и k, необходимо измерить периоды колебаний Тр пустой рамки и Тэ рамки с закрепленным в ней эталонным образцом, момент инерции
Iэ которого известен. При этом
| | Tp=2π | (6) |
| | Tэ=2π | (7) |
Из последних соотношений вытекает расчетная формула для момента инерции исследуемого образца
| | | (8) |
7.2 Экспериментальная установкаУстановка (рисунок 7.1) состоит из натянутой между двумя кронштейнами стальной проволоки, на которой подвешена легкая рамка, электромагнита и собранных в одном корпусе универсального электронного миллисекундомера и счетчика колебаний. Последние соединены с ф/э датчиком. В комплекте имеются три образца, один из которых мы условно принимаем за эталонный.
По обеим сторонам рамки расположены два флажка из магнитного материала.
На лицевой панели секундомера размещены клавишные выключатели СЕТЬ, ПУСК, СБРОС и СТОП, а также цифровые индикаторы, которые высвечивают время t и число n полных колебаний маятника.
7
 .3 Выполнение экспериментa
.3 Выполнение экспериментa7.3.1 Выравнить прибор и включить его в сеть.
7.3.2Закрепить исследуемый образец в рамке.
7.3.3 Поворачивая рамку, приблизить ее флажок к электромагниту. Последний притягивает к себе флажок, фиксируя тем самым маятник в начальном положении.
7.3.4 Нажать последовательно клавиши СБРОС и ПУСК. Цепь электромагнита при этом размыкается и маятник начинает совершать свободные колебания.
Рисунок 7.1
7.3.5 Определить t0 – время 20-30 полных колебаний. Для этого надо нажать клавишу СТОП при появлении на счетчике колебаний числа, на единицу меньшего, т.е. равного (n – 1). После остановки счетчика, считать показания секундомера и занести в таблицу. 7.3.6 Заменить исследуемый образец на эталонный и определить t