Файл: Решение задач с применением графов при подготовке к огэ по информатике.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 129

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Решение задач с применением графов при подготовке к ОГЭ по информатике
Цель: Показать учащимся многообразие задач, решаемых с использованием теории графов.

Задачи: Систематизировать и расширить представления учащихся о графах; формировать познавательный интерес к изучению информатики; развивать мыслительные процессы учащихся (анализ, систематизация, классификация)

Ходурока:

Организационный момент. Приветствие учащихся, проверка готовности к уроку. Домашнее задание – пробный вариант ОГЭ. Тетради с решением собрать в конце урока. С вопросами можно подойти на кружковом занятии (7 урок).

Мотивационный момент.

Вместо предисловия

ЕГЭ по информатике нельзя назвать легким экзаменом. За последние пять лет число школьников, сдающих Единый государственный экзамен по информатике, увеличилось более чем в полтора раза.

В нашей школе учащиеся очень часто стали выбирать экзамены по информатике.

При подготовке к ОГЭ и ЕГЭ у многих учащихся возникают трудности при решении тех или иных задач, однако, многие типы задания можно решить очень просто с помощью графов.
Определения выучить

1. Граф – это наглядное средство представления состава и

структуры системы.

2. Граф – это конечное множество точек, некоторые из которых соединены линиями.

3. Точки – называются вершинами, а соединяющие их линии – ребрами.

4. Цепь – это путь по вершинам и ребрам графа, включающий любое ребро не более одного раза.

5. Ориентированный граф – это граф, вершины которого соединены дугами. С помощью таких графов могут быть представлены схемы односторонних отношений.

6. Цикл – это цепь, начальная и конечная вершины которой совпадаю. Граф с циклами называют сетью.

7. - Что такое дерево? Ответ: Дерево – это граф, представленный в виде иерархической системы.

8. Взвешенный граф – это граф, у которого вершины или ребра (дуги) характеризуются некоторой
На слайде задание Пример 1. Какая модель позволяет легко и просто решать такие задачи? Граф. В ОГЭ по информатике для 9 класса 3 типа задач можно легко решить, используя теорию графов. Для начала вспомним, что называют графом.

Граф – это множество точек, соединенных линиями. Точки – это вершины графа, линии – ребра. Граф называется древовидным, если для каждой пары вершин существует только одно соединяющее ребро.

Первый тип задач – задания В3.
A
B
C
D
E
F

A



3
5






15

B
3






4






C
5






1






D



4
1



2
6

E









2



1

F
15






6
1





Пример 1. Между населѐнными пунктами A, B, C, D, E, F построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице.


1) 9
2) 11
3) 13
4) 15



Определите длину кратчайшего пути между пунктами A и F. Решение:

  1. Точками A, B, C, D, E, F, расположенными по кругу, обозначим населенные пункты.

  2. Если в таблице есть число, соединяем точки отрезком и подписываем сверху это число.

  3. Отмечаем конечный пункт (в нашем случае это F) и рассматриваем пункты, из которых можно в него попасть. (в нашем случае это A, E, D). В свою очередь в пункт E можно попасть из D, а в пункт D – из C и B. В пункты C и B попадаем из A. Получили начальный пункт. Изобразим дерево всех возможных путей из A в F.

  4. Вычислим длины полученных дорог.

  5. AF=15, ACDEF=9, ABDEF=10, ACDF=12, ABDF=13.

  6. Выбираем длину кратчайшего пути – 9, в предложенных вариантах это ответ №1.

Ученик у доски

Пример 2. Между населѐнными пунктами A, B, C, D, E построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице.
A
B
C
D
E

A



2
5
1



B
2



1






C
5
1



3
2

D
1



3






E






2







1) 4
2) 5
3) 6
4) 7



Определите длину кратчайшего пути между пунктами A и E. Ответ: №2.

Среди задач В3 также встречаются такие вариации, которые требуют для решения только внимательности учащегося.

Пример 3. В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите граф, соответствующий таблице.



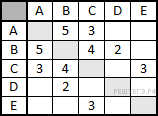
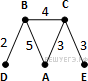
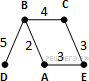
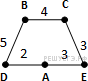
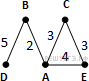
Пример 4. В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите граф, соответствующий таблице.




Второй тип задач – задания В11.

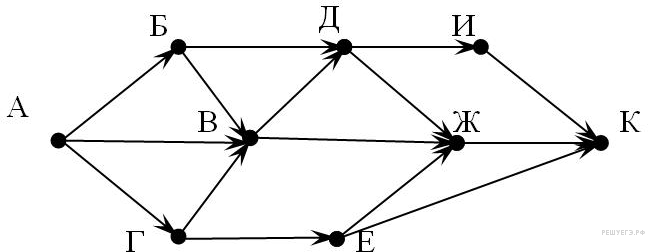Пример 5. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Решение:


Вершина
Предшествующие вершины
Количество путей

Б
А
1

В
А+Б
1+1=2

Г
А
1

Д
Б+В
1+2=3

Е
Г
1

Ж
Д+В+Е
3+2+1=6

И
Д
3

К
И+Ж+Е
3+6+1=10



Подсчитаем количество путей, последовательно для каждой из вершин графа. Заполним таблицу:

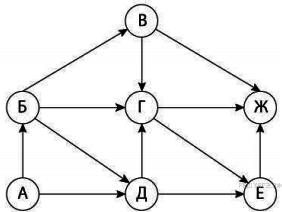Ответ: 10 различных путей. Ученик у доски

Пример 6. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение: Подсчитаем количество путей, последовательно для каждой из вершин графа. Заполним таблицу:

Вершина
Предшествующие вершины
Количество путей

Б
А
1

В
Б
1

Г
Б+В+Д
1+1+2=4

Д
А+Б
1+1=2

Е
Г+Д
4+2=6

Ж
В+Г+Е
1+4+6=11

Ответ: 11 различных путей.
Пример 7. У исполнителя Вычислитель две команды, которым присвоены номера:

  1. умножь на 4


  2. вычти 3

Первая из них увеличивает число на экране в 4 раза, вторая уменьшает его на 3.

Составьте алгоритм получения из числа 2 числа 14, содержащий не более 5 команд. В ответе запишите только номера команд.

Решение:

№ п/п
Номер команды
Действие
Результат

1
1
2*4
8

2
2
8-3
5

3
1
5*4
20

4
2
20-3
17

5
2
17-3
14

Это было решение, основанное на свойствах делимости чисел, и требует логических размышлений. Есть еще способ решения, основанный на применении графов. Возможно, вам будет проще решать задачи, используя его.


2

8

5
32

2
20
29






17






14





Составим дерево возможных решений.
Полученное решение 2-8-5-20-17-14, осталось записать его с помощью команд 12122. Ученик у доски.

Пример 8. У исполнителя Вычислитель две команды, которым присвоены номера:

  1. умножь на 3


  2. прибавь 1

Первая из них увеличивает число на экране в 3 раза, вторая увеличивает его на 1. Составьте алгоритм получения из числа 5 числа 60, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.
Подводим итог. Графы значительно упрощают решение некоторых задач. Оставшееся время выполняем самостоятельную работу.

Самостоятельная работа. Вариант 1


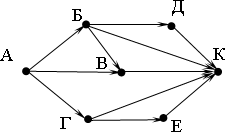  1. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 6)

  2. Между населѐнными пунктами A, B, C, D, E, F построены дороги, протяжѐнность которых (в километрах) приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице.

Определите длину кратчайшего пути между пунктами A и F.

1) 7 2) 9 3) 11 4) 15
A
B
C
D
E
F

A



1
5






15

B
1



2









C
5
2



1






D






1



2
6

E









2



1

F
15






6
1



Ответ: 7

  1. У исполнителя Квадратор две команды, которым присвоены номера:

    1. возведи в квадрат


    2. прибавь 3

Первая из них возводит число на экране во вторую степень, вторая увеличивает его на 3. Составьте алгоритм получения из числа 1 числа 25, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

(Ответ: 21222)

Самостоятельная работа. Вариант 2


  1. На рисунке –– схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? Ответ: 7

Смотрите также файлы