Файл: Коммуникаций федеральное государственное бюджетное образовательное учреждение высшего образования.docx
Добавлен: 10.01.2024
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)
Факультет Инфокоммуникационных сетей и систем Кафедра Защищенныхсистемсвязи
Дисциплина Криптографические методы защиты информации
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6
Изучение булевых функций и их свойств
(темаотчета)
Информационнаябезопасность(10.03.01)
(кодинаименованиенаправления/специальности)
Студент группы ИКБ-03:
Шанин П.С.
(Ф.И.О.) (подпись)
Д.т.н., проф. каф. ЗСС:
Яковлев В.А.
(Ф.И.О.) (подпись)
Цель работы: Получение практических навыков по изучению свойств БФ f(x1,x2,x3) и булевых функций, используемых в нелинейном преобразовании алгоритма «Кузнечик» стандарта ГОСТ 34.12-2015.
Используемое программное обеспечение: В работе используется электронный документ «Исследование БФ.xlsx», разработанный в Microsoft Excel – программа для работы с электронными таблицами.
Ход выполнения лабораторной работы:
Часть 1.
Булевой функцией (БФ) называется отображение {0,1}n {0,1}, т. е. сопоставление вектору из n бит значение 0 или 1. Задать БФ от n переменных можно, указав значение функции на каждом из наборов значений переменных. Булева функция может быть задана таблицей истинности. В лабораторной работе булева функция задана согласно варианту студента в списке группы – 20 вариант.
Таблица 1 – Булева функция
| Аргумент | Номер варианта | ||
| X3 | X2 | X1 | 20 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Вторым этапом выполнения лабораторной работы является нахождение полинома Жегалкина. Любая булева функция может представляться в виде алгебраической нормальной формы – АНФ. Алгебраическую нормальную форму также называют полиномом Жегалкина: fn = y0·1 ⨁ y1·x1 ⨁ y2·x2…⨁y12·x1·x2…⨁y1..n·x1..xn.
Заданная БФ:
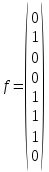
Построили матрицу An = [8*8] рекуррентным образом:
An =
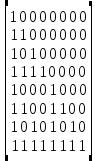
Для нахождения коэффициентов уi, необходимо перемножить две матрицы An и f(x) и от каждого элемент полученной матрицы найти остаток от деления на 2:
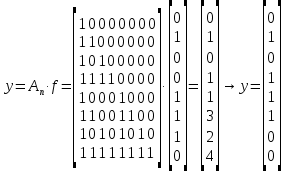
После перемножения двух матриц получаем столбец коэффициентов y0, y1 … y123. Для более удобного восприятия, запишем столбец в транспонированном виде:
Таблица 2 – Коэффициенты
| X1 | X2 | X3 | y | Переменные |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | х3 |
| 0 | 1 | 0 | 0 | х2 |
| 0 | 1 | 1 | 1 | x2х3 |
| 1 | 0 | 0 | 1 | х1 |
| 1 | 0 | 1 | 1 | х1х3 |
| 1 | 1 | 0 | 0 | х1х2 |
| 1 | 1 | 1 | 0 | х1х2х3 |
Таким образом, АНФ булевой функции имеет вид:
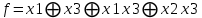
В следующем этапе лабораторной работы необходимо определить вес БФ. Вес БФ - число единиц среди его элементов. Таким образов вес представленной БФ = 4.
Четвёртый этап – найти нелинейность исследуемой БФ. Термин «нелинейность» принят для оценки степени нелинейности
, использующей понятия веса и расстояния Хэмминга. Расстоянием Хэмминга это число, равное количеству позиций, в которых различаются соответствующие символы двух функций одинаковой длины т.е., это число позиций, на которых f(x) не равно g(x).
Нелинейность находится по формуле:
N(f) = 2n-1 -
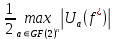
Для количественной оценки нелинейности в первую очередь необходимо найти спектры Уолша-Адамара (ПУА).
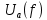это преобразование ПУА от БФ. 
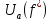это ПУА для сопряженной булевой функции, которое представлено в виде: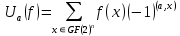 
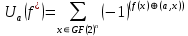
где a это векторный параметр, принимающие все возможные комбинации 1 и 0.
Первое, что необходимо сделать для нахождения нелинейности БФ это найти скалярное произведение b= (а, х). Скалярное произведение в координатах ищется по формуле:
b = a1x1; a2x2;…;anxn.
Таблица 3 - Таблица векторов x и а.
| | x | a | | ||||
| x0 | 0 | 0 | 0 | 0 | 0 | 0 | a0 |
| x1 | 0 | 0 | 1 | 0 | 0 | 1 | a1 |
| x2 | 0 | 1 | 0 | 0 | 1 | 0 | a2 |
| x3 | 0 | 1 | 1 | 0 | 1 | 1 | a3 |
| x4 | 1 | 0 | 0 | 1 | 0 | 0 | a4 |
| x5 | 1 | 0 | 1 | 1 | 0 | 1 | a5 |
| x6 | 1 | 1 | 0 | 1 | 1 | 0 | a6 |
| x7 | 1 | 1 | 1 | 1 | 1 | 1 | a7 |
Таблица 4 – Скалярное произведение векторов
| xi, a0 | xi, a1 | xi, a2 | xi, a3 | xi, a4 | xi, a5 | xi, a6 | xi, a7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Таблица 5 –
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Таблица 6 – (-1) в степени
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 |
| 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 |
| -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 |
| -1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 |
| -1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
Таблица 7 – Сумма
| 0 | 0 | -4 | 4 | 4 | 4 | 0 | 0 |
Получаем, что максимальный ПАУ по модулю равен 4:
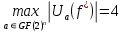.Таким образом нелинейность рассчитывается по формуле:
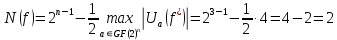
Существует граница значений нелинейности:
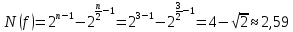
В следующем этапе лабораторной работы необходимо рассчитать коэффициент корреляции. Коэффициентом корреляции R(i,j) между двумя булевыми функциями называется величина:
R(i,j) =
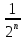∑ (fi*( 
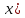∙ fj*(x)),где f*(x) - сопряженная функция к булевой функции.