Файл: Коммуникаций федеральное государственное бюджетное образовательное учреждение высшего образования.docx
Добавлен: 10.01.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Так как функция значение функции f(x) соответствует 20 варианту, следовательно по условию лабораторной работы значение g(x) должно соответствовать 21 варианту.
Таблица 8 – Расчёт коэффициента корреляции
| f(x) | g(x) | f*(x) | g*(x) | f*(x) ∙ g*(x) | Сумма ∑ | Коэф. корреляции |
| 0 | 0 | 1 | 1 | 1 | 4 | 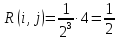 |
| 1 | 1 | -1 | -1 | 1 | ||
| 0 | 1 | 1 | -1 | -1 | ||
| 0 | 0 | 1 | 1 | 1 | ||
| 1 | 1 | -1 | -1 | 1 | ||
| 1 | 0 | -1 | 1 | -1 | ||
| 1 | 1 | -1 | -1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 |
Проверили правильность расчетов, используя электронный документ «Исследование БФ.xlsx» лист №1 (рис.1 – 4).
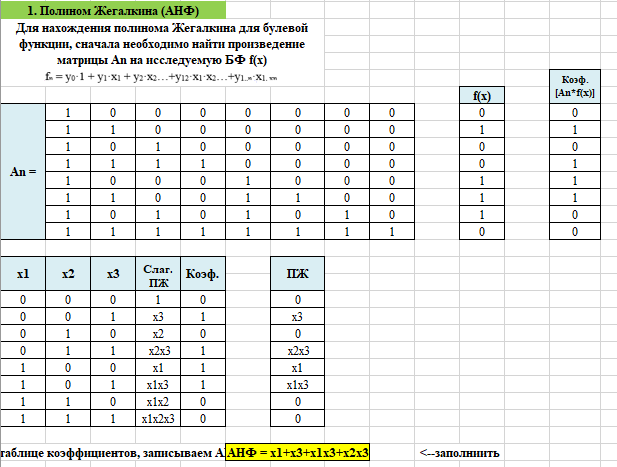
Рисунок 1 – Проверка расчёта полинома Жегалкина (АНФ)
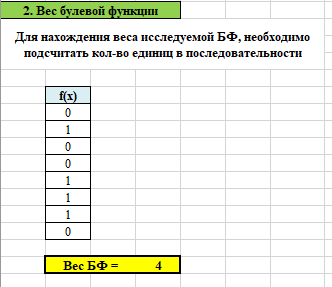
Рисунок 2 – Проверка нахождения веса булевой функции

Рисунок 3 – Проверка расчёта нелинейности булевой функции
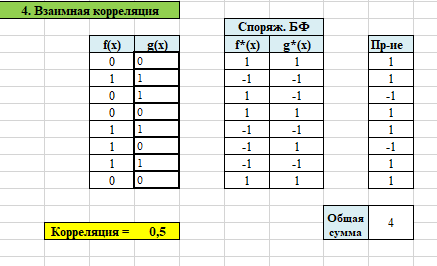
Рисунок 4 – Проверка расчёта коэффициента корреляции
Часть 2.
Исследовать булеву функцию fn(x) (согласно варианту), которая используется в нелинейном преобразовании ГОСТ P-34.12-2015, на уравновешенность. Булева функция для 20 варианта:
f3(x) =1110110010110001100101110001011011010110011010110001011001 111001101011110110111100101100100010100001011000111100001110111000011010011101010010100111100111101011000010001110010010000101100110010100011000101101010111111010110000001111110010101000000000101100
Нашли и записали полную АНФ для заданной булевой фикции, используя таблицы произведений функции и матрицы An на странице «АНФ» документа «Исследование БФ.xlsx» (рис.5).
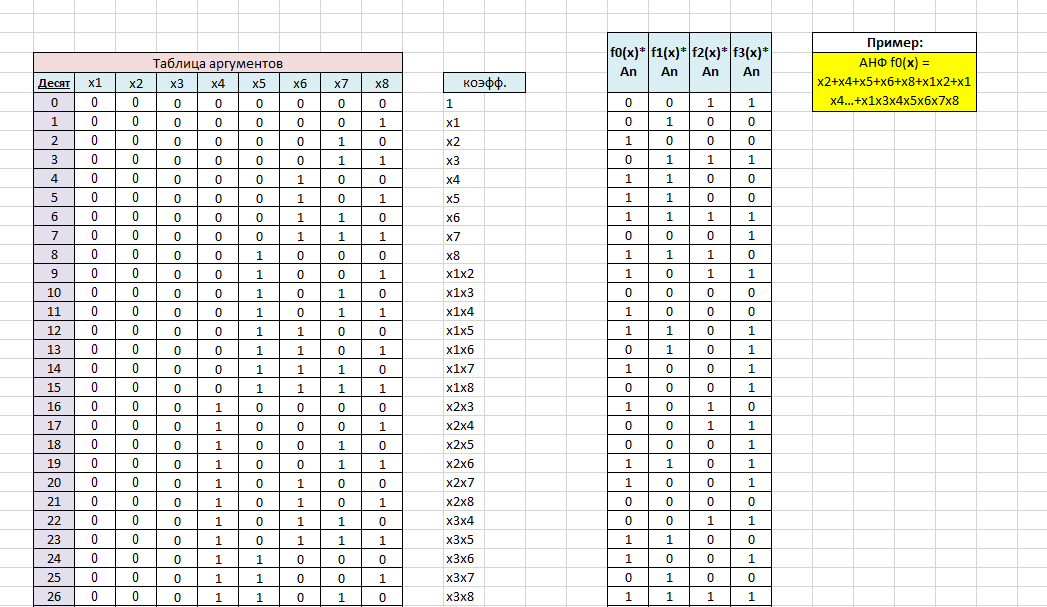
Рисунок 5 – Поиск полной АНФ для f3(x)
Полная АНФ: 1+x3+x6+x7+х1х2+х1х5+х1х6+х1х7+х1х8+х2х4+х2х5+х2х6+х2х7+х3х4+х3х6+х3х8+
х4х5+x5x6+x6x7+x7x8+х1х2х3+х1х2х4+х1х2х6+х1х3х4+х1х3х5+х1х3х8+х1х4х5+х1х4х6+
х1х4х8+х2х3х6+х2х4х5+х2х4х7+х2х5х6+х2х5х8+х2х6х7+х2х6х8+х2х7х8+х3х4х5+
х3х4х6+х3х5х6+х3х5х8+х3х6х7+х4х5х8+х4х7х6+х4х6х8+х4х7х8+x5x6x7+x5x7x8+
х1х2х3х6+х1х2х3х7+х1х2х3х8+х1х2х4х5+х1х2х4х6+х1х2х4х7+х1х2х4х8+х1х2х5х7+
х1х3х4х5+х1х3х4х6+х1х3х6х7+х1х3х7х8+х1х4х5х7+х1х4х5х8+х2х3х4х6+х2х3х4х7+
х2х3х4х8+х2х3х5х7+х2х3х5х8+х2х3х6х8+х2х3х7х8+х2х4х5х6+х2х4х5х7+х2х4х6х8+
х2х4х7х8+х2х5х6х7+х2х5х6х8+х2х5х7х8+х3х4х5х7+х3х4х5х8+х3х4х6х8+х3х4х7х8+
х3х5х6х7+х4х5х7х8+х4х6х7х8+х1х2х3х4х7+х1х2х3х5х7+х1х2х3х6х7+х1х2х3х6х8+
х1х2х4х5х6+х1х2х4х5х7+х1х2х4х6х7+х1х2х4х7х8+х1х2х5х6х7+х1х2х5х6х8+х1х3х4х5х7+х1х3х4х5х8+х1х3х4х6х8+х1х3х6х7х8+х1х4х5х6х7+х1х4х5х6х8+х2х3х4х5х7+х2х3х4х6х8+х2х3х4х7х8+х2х3х5х7х8+х3х4х5х6х7+х3х5х6х7х8+х4х5х6х7х8+х1х2х3х4х6х8+
х1х2х3х5х6х7+х1х2х3х6х7х8+х1х2х4х5х6х7+х1х2х4х6х7х8+х1х2х5х6х7х8+
х1х3х4х5х6х7+х1х3х4х6х7х8+х1х3х5х6х7х8+х2х3х4х5х6х7+х2х3х4х6х7х8+
х2х4х5х6х7х8+х1х2х3х4х5х6х7+х1х2х3х4х5х6х8+х1х2х3х4х5х7х8+х1х2х3х5х6х7х8
Нашли преобразование Уолша-Адамара и далее нелинейность для функции f3(x) используя лист «ПУА» документа «Исследование БФ.xlsx» (рис.6). Рассчитали границу нелинейности по формуле.
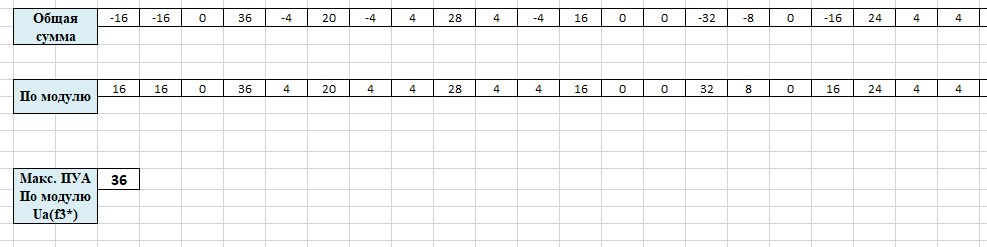
Рисунок 6 – Преобразование Уолша-Адамара для f3(x)
Таким образом нелинейность рассчитывается по формуле:
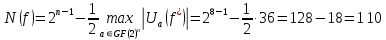
Существует граница значений нелинейности:
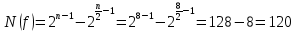
Убедились, что коэффициент взаимной корреляции между сопряженными функциями, которые используются в нелинейном преобразовании ГОСТ P-34.12-2015 равен нулю, используя лист «Вз. Корр.» документа «Исследование БФ.xlsx» (рис.7), рассчитали коэффициент корреляции.
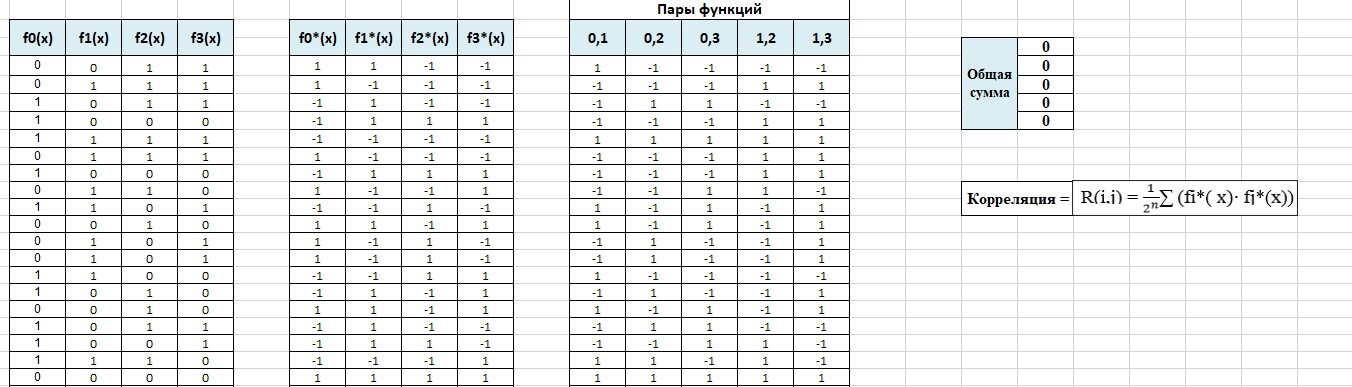
Рисунок 7 – Взаимная корреляция
Расчёт коэффициента корреляции:
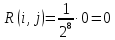
Коэффициент корреляции отсутствует и это говорит о том, что функции полностью независимы друг от друга.
Вывод: В ходе выполнения лабораторной работы были получены практические навыки по изучению свойств булевых функций f(x1,x2,x3) и булевых функций, используемых в нелинейном преобразовании алгоритма «Кузнечик» стандарта ГОСТ 34.12-2015. Успешно удалось рассчитать полином Жегалкина для булевой функции, определить вес представленной функции. Ещё одним свойством булевой функции является нелинейность. Термин «нелинейность» принят для оценки степени нелинейности, использующей понятия веса и расстояния Хэмминга. С помощью расчёта взаимной корреляции двух булевых функций смогли установить их независимость друг от друга (в случае если коэффициент равен 0) или зависимость (если коэффициент отличен от 0).
Санкт-Петербург 2023 г