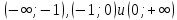Задание 2

РАЗДЕЛ № 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Задача 1.

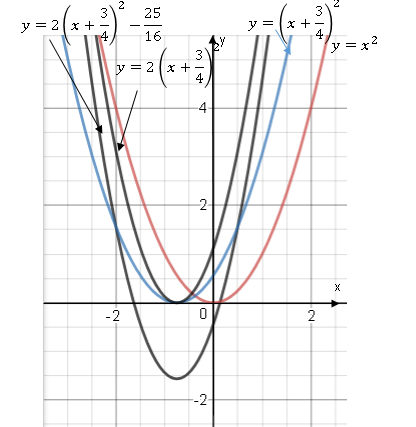
Построить графики функций.





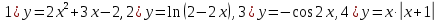
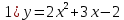
Выделим полный квадрат





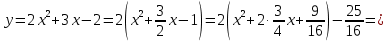
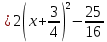
Преобразования квадратичной функции выглядят так:



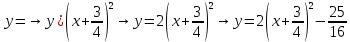
Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль Оу вдвое, сдвигается влево на 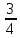  и вниз на  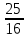 единицы.

Получили требуемый график.





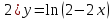
Преобразования логарифмической функции выглядят так:



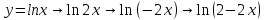
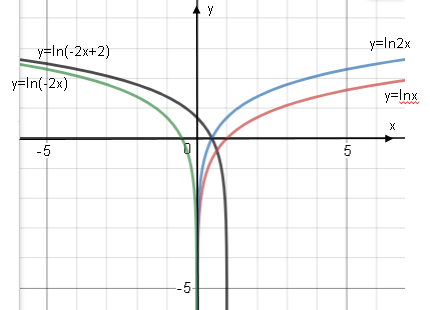
Изобразим график исходной логарифмической функции

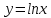
Производим растягивание вдоль в 2 разы Ох.

Производим отображение относительно Оу.

Производим сдвиг на 2 единицы влево.

Получили требуемый график.





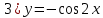
Преобразования функции выглядят так:

.

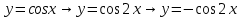
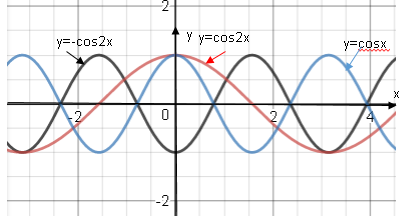
Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль Оx вдвое, отображается симметрично относительно Oy.

Получили требуемый график.

---

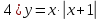
С 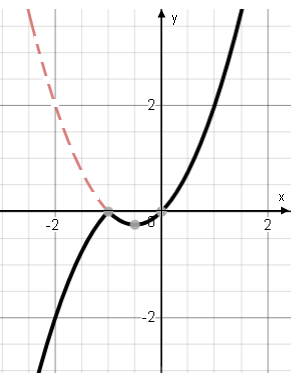троим график функции 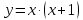и там, где 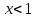т.е. на интервале 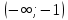(вместо графика 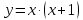) строим изображение симметричное графику 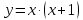относительно оси абсцисс.

Задача 2. Записать уравнения кривых в полярных координатах и построить их.



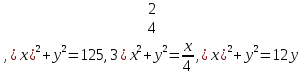
Решение

►1)

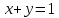
Заменяя 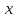и у на r и  по формулам 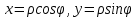получим: 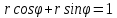или .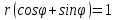





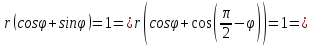
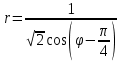
По условию прямая не проходит через начало координат, поэтому ее расстояние r от начала координат отлично от 0. Тогда из последнего равенства следует, что при любом  и .

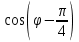Полярное уравнение данной прямой



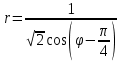
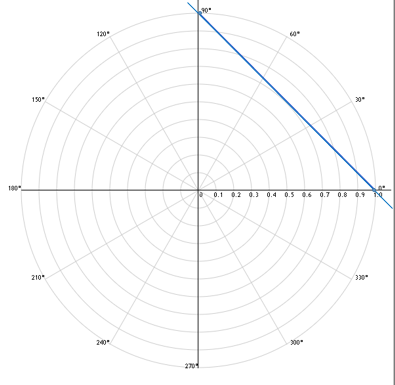
Построим график функции по двум точкам.





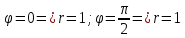
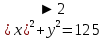
Заменяя 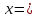и у на r и  по формулам 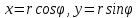получим: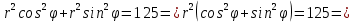



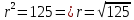
Построим график функции по точкам.

---

►

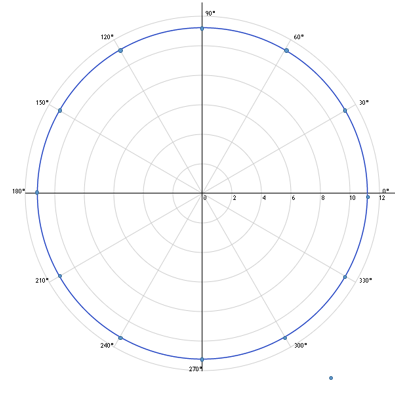
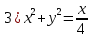
Заменяя и у на r и  по формулам получим: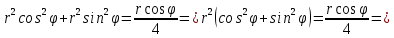



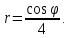
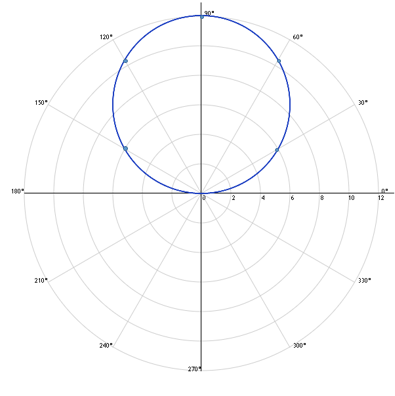
Для построения кривой в ПСК вычислим значения функции
в точках 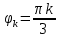0, 1, …, 12, входящих в область определения, т. е.в точках, где выполнено условие 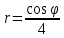, и заполним

k		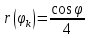,	k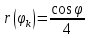
0	0	0,25	–	–	–
1	π/6	0,216	4	10π/6	0,125
2	2π/6	0,125	5	11π/6	0,216
3	π/2	0	6	12π/6	0б25

Построим график функции по точкам



►

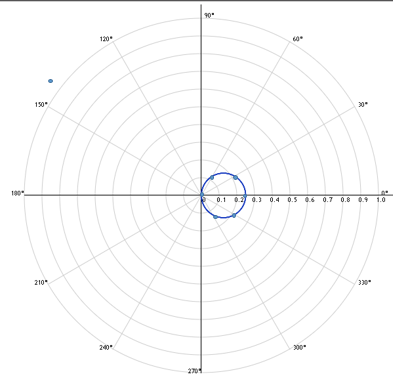
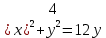
Заменяя и у на r и 

---

по формулам 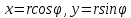получим: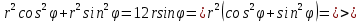



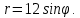
Для построения кривой в ПСК вычислим значения функции
в точках 0, 1, …, 12, входящих в область определения, т. е.в точках, где выполнено условие 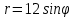, и заполним

k		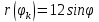,	k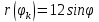
0	0	-	–	–	–
1	π/6	6	4	4π/6	10,39
2	2π/6	10,39	5	5π/6	6
3	π/2	12	6	6π/6	0

Задача 3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.





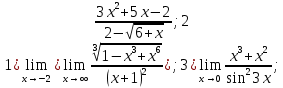
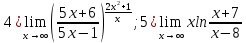
Решение

---

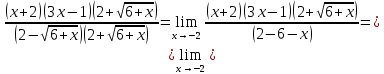
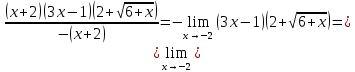
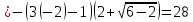
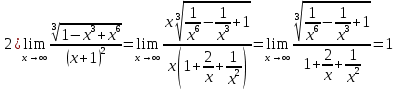
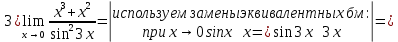
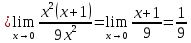
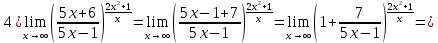
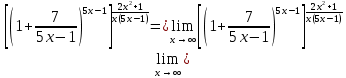
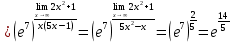
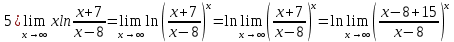
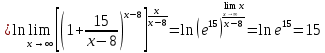
Задача 4. Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.



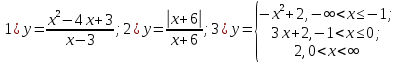
Решение



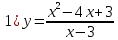
Функция не определена в точке x=3. 

Вычислим односторонние пределы:





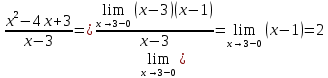
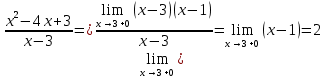
Односторонние пределы конечны и равны.

Таким образом, в точке 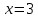  функция терпит устранимый разрыв.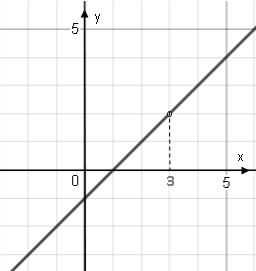



 2) Функция определена и непрерывна при всех x, за исключением точки

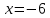  , где существует разрыв. Исследуем точку разрыва.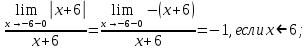





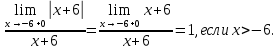
Так как значения односторонних пределов конечны, то, следовательно, в точке 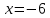  существует разрыв первого рода.

В этой точке разрыва функция имеет скачек:



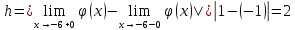
График функции схематически показан на рисунке



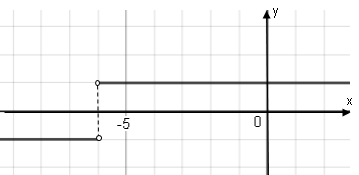
3)Функция 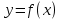определена при 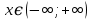и непрерывна на интервалах

---

Смотрите также файлы

• Практическая ра.docx

• Для практической работы по модулю.docx

• Дайте характеристику основным теориям личности по А. Н. Леонтьеву, А. Г. Ковалеву, К. К. Платонову, С. Л. Рубинштейну.docx

• Что мы Родиной зовём.docx

• Практическая работа 1 к разделу 1 Ценности и их роль для человека и общества Практическая работа состоит из двух частей.docx