ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 59
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего
образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИТМО»
Выполнили:
Студентки группы U312121
Камышева Е.В. Записецкий В.С.
Лабораторная работа №2
Проверила: Мишура Людмила Геннадьевна
Дата:
Оценка:
Специальность: 38.03.05 Бизнес-информатика
09.02.03 Программирование в компьютерных системах
Санкт-Петербург 2022
Исходные данные:
Данные о динамике цен на платину в долларах США за тройскую унцию в течение года.
Цель работы: Расчет динамических характеристик ряда, выявление и описание тренда; прогнозирование на основе экстраполяции тренда.
Ход работы: В нашей работе представлен динамический ряд. Динамический ряд – это последовательность упорядоченных во времени значений одноименного статистического показателя. Он состоит из двух элементов: tiи соответствующего ему уровня развития явления yi,.
Исходные данные можно увидеть в Приложении(таблица 1).
Подсчет динамических характеристик ряда:
1.Подсчет индивидуальных характеристик ряда.
Мы начали свою работу с расчета абсолютного цепного и базисного прироста для всех месяцев кроме первого. Абсолютный цепной прирост мы рассчитывали по формуле: Δyцi= yi-
yi-1. Абсолютный базисный прирост по формуле: Δyбi = yi - y1.
Далее, используя полученные ранее данные, мы рассчитали базисный коэффициент, темп роста и цепной коэффициент, темп роста. Делали мы это по четырем формулам:
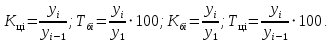
Потом мы рассчитали абсолютное значение одного процента по формуле:
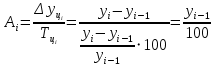.Полученные данные можно увидеть в Приложении(таблица 2).
Также по исходным данным, нами был построен график:
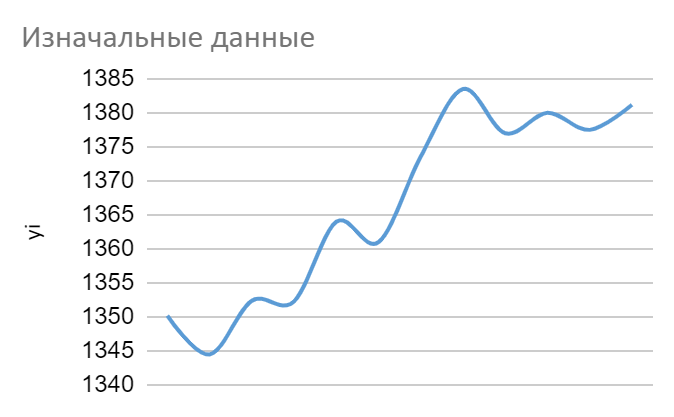
Рисунок 1. Исходные данные.
2. Подсчет обобщающих характеристик ряда динамики.
Далее нам необходимо рассчитать средний уровень ряда. Делаем это мы по формуле средней арифметической простой:
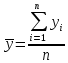.Рассчитываем среднее абсолютное изменение уровней по формуле:
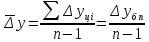. Рассчитываем средний коэффициент роста и прироста по формулам:
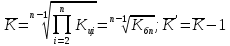
Рассчитываем дисперсию уровней динамического ряда и среднее квадратическое отклонение уровней по двум формулам:
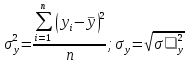
Последние, что мы находим из обобщающих характеристик ряда – это коэффициент вариации уровней ряда динамики по формуле:
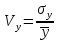.Все эти характеристики можно увидеть в Приложении (таблица 3)
3. Анализ динамического ряда.
Для выявления и оценки основной долговременной тенденции развития или тренда, мы использовали три способа: метод укрупнения интервалов, метод скользящей средней и метод аналитического выравнивания.
Метод укрупнения интервалов означает увеличение данных интервалов и расчет новых значений уровня, как среднее арифметическое по этому интервалу. В нашей работе исходные интервалы были увеличены в 3 раза. Полученные интервалы и новые значения можно увидеть в Приложении (таблица 4). Графическое представление можно увидеть на рисунке 1.
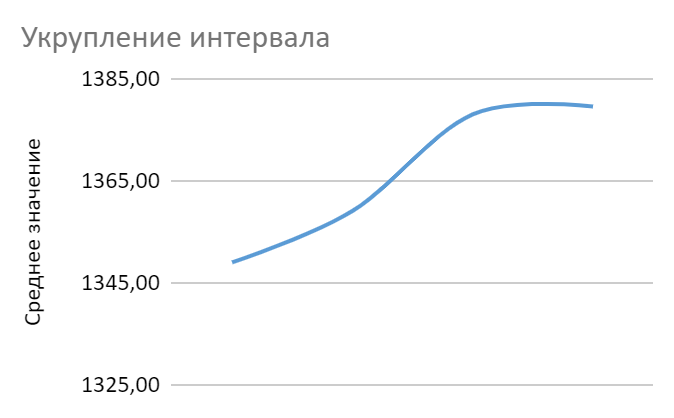
Рисунок 2. Метод укрупнения интервалов.
Метод скользящей средних заключается в замене уровней исходного ряда теоретическими уровнями, рассчитанными по формуле скользящей средней. Период скольжения был взят равный 3. Скользящая средняя при периоде равным 3вычисляется по формуле:
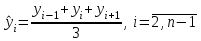. Расчеты можно найти в Приложении (таблица 5). Графическое представление можно увидеть на рисунке 2.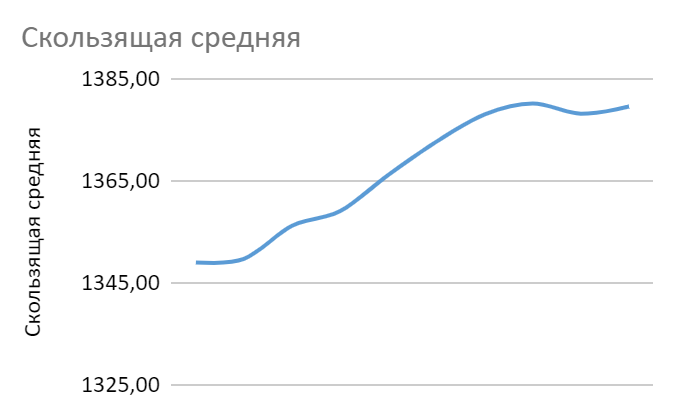
Рисунок 3. Метод скользящей средней.
Следующий и последний метод – это метод аналитического выравнивания. Проанализировав два предыдущих графика, мы пришли к выводу, что имеем дело с показательной функцией:
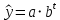. Что бы построить график аналитического выравнивания, надо рассчитать параметры по методу наименьших квадратов, перед этим осуществив линеаризацию функций и значений ряда.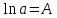
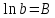
При этом коэффициенты A и B мы находили через линейную зависимость:
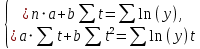
График получившегося распределения можно увидеть на рисунке 4. Числовые значения в Приложении (таблица 6).
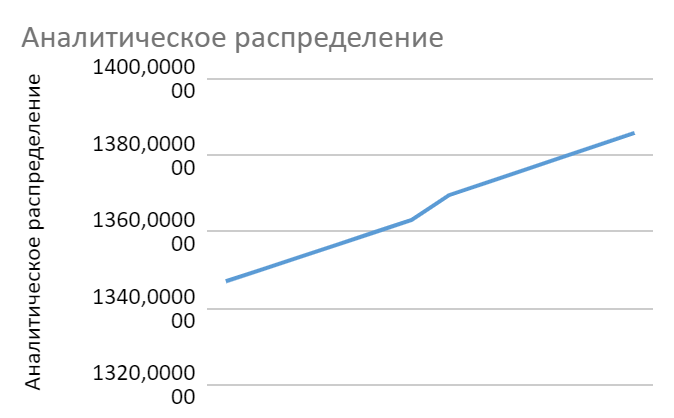
Рисунок 4. Метод аналитического выравнивания.
4. Проверка на надежность через критерий Фишера.
Построенную раннее трендовую модель проверяем на надежность корреляционной связи. Для этого используем критерий Фишера, по-другому этот критерий называется F-критерий. Он вычисляется по формуле:
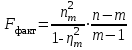, где 
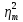– это теоретический коэффициент детерминации, а m – это количество параметров трендового уравнения. Теоретический коэффициент детерминации рассчитывается по формуле:
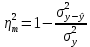, где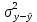 
– это остаточная дисперсия уравнений. Находится она по формуле: 
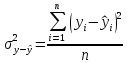. Теоретический коэффициент детерминации в нашей работе равен 0,9998, а критерий Фишера 9,997. Надежность системы проверяется сравнением фактического уровня F-критерия с табличным (критическим) уровнем. В нашем случае табличный уровень равен 4,96. Это меньше, чем фактический. Отсюда можно сделать вывод, что система надежна.
5.Прогнозирование на основе экстраполяции тренда.
Предыдущие действия дали нам основание для дальнейшего прогнозирования и определения возможных значений ряда динамики в будущем. В статистике есть два вида прогноза: точечный и интервальный. Для прогнозирования используются разные методы экстраполяции: на основе среднего абсолютного прироста, на основе среднего коэффициента роста, на основе аналитического выравнивания ряда.
Метод прогнозирования на основе среднего абсолютного прироста применяется в том случае, если уровни ряда динамики изменяются равномерно (линейно).
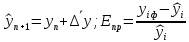
При I=1 y12+1 = 1384.018 E=0,1097
При I=3 y12+3 = 1389.655 Е=0,3997
В обоих случаях Е<10 – Высокая.
Прогнозирование на основе аналитического выравнивания
Интервальный прогноз предполагает определение величина его доверительного интервала:
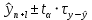
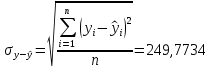; ta – коэффициент доверия по распределению Стьюдента. В нашей работе равен ta = 2.228.y12+1 = от 827,523 до 1940,513
y12+3 = от 1389.655 до 1946,150
Наш статистические данные попадают в эти промежутки, следовательно прогноз точный.
6. Вывод
Мы исследовали динамический ряд, который по отношению ко времени является интервальным. Интервал – месяц. Наш статистический признак – стоимость платины. Мы представили наш ряд графически, аналитически и таблично. Изучив обобщающие статистические признаки, мы сделали вывод, что средним значением является 1366,5 , на 2.82 в среднем увеличивается уровень ряда в месяц, в 0,929 в среднем за месяц растет уровень динамического ряда, в среднем на 179,637 отклоняются значения от среднего, коэффициент вариации меньше 33 процентов, значит наш ряд однородный. Цепные абсолютные приросты на
протяжении всех месяцев не только положительные, значит, наши значения не только растут, но и уменьшаются.
Также в работе мы рассмотрели 3 метода выявления тренда. Сначала метод укрупнения интервалов, где объединили месяца в кварталы и также пришли к выводу, что наша тенденция – стабильный рост. Затем метод скользящей, где у нас не сглаживаются первое и последнее значение ряда. Но мы также пришли к выводу, что у нашего ряда тенденция роста. Последним методом было аналитическое выравнивание, где мы нашли показательную временную функцию, на основе которой получили теоретические уровни ряда. Построив график, мы пришли все к тому же выводу. Чтобы проверить надежность подобранной нами функции, мы воспользовались коэффициентом Фишера.
Далее мы считали прогнозы на месяца и 3 месяца вперед. Сначала точечные на основе среднего абсолютного прироста и на основе аналитического выравнивания. Проверили относительную ошибку прогноза и получили высокую интерпретацию показателя, что свидетельствует о точности наших прогнозов.
Потом мы считали интервальный прогноз, который является более точным, потому что учитывает вероятность свершения, в отличии от точечного прогноза. Получили интервалы, в которые входят данные нам значения на месяц и три месяца вперед. Следовательно интервальный прогноз также является точным.
Итого, наш ряд обладает тенденцией к стабильному росту. А построенные нами прогнозы являются точными
Приложение
| Динамика цен на платину в долларах СЩА за тройскую уницую | ||||||||||||
| дата | 01.01 | 01.02 | 01.03 | 01.04 | 01.05 | 01.06 | 01.07 | 01.08 | 01.09 | 01.10 | 01.11 | 01.12 |
| цена | 1350,2 | 1344,5 | 1352,4 | 1352,3 | 1364 | 1361 | 1373,6 | 1383,5 | 1377 | 1380 | 1377,5 | 1381,2 |
Таблица 1. Исходные данные.
| Абсолютный прирост | Коэффициент роста | Коэффициент прироста | Темп прироста | Абсолютное значение одного процента прироста | ||||||
| цепные | базисные | цепные | базисные | цепные | базисные | |||||
| ∆yiц | ∆yiб | Kiц | Kiб | ∆Kiц | ∆Kiб | ∆Tiц | Ai | |||
| | | | | | | | | |||
| -5,70 | -5,7 | 0,9958 | 0,9958 | -0,0042 | -0,0042 | -0,4221597 | 13,502 | |||
| 7,90 | 2,2 | 1,0059 | 1,0016 | 0,0059 | 0,0016 | 0,5875790 | 13,445 | |||
| -0,10 | 2,1 | 0,9999 | 1,0016 | -0,0001 | 0,0016 | -0,0073943 | 13,524 | |||
| 11,70 | 13,8 | 1,0087 | 1,0102 | 0,0087 | 0,0102 | 0,8651926 | 13,523 | |||
| -3,00 | 10,8 | 0,9978 | 1,0080 | -0,0022 | 0,0080 | -0,2199413 | 13,640 | |||
| 12,60 | 23,4 | 1,0093 | 1,0173 | 0,0093 | 0,0173 | 0,9257899 | 13,610 | |||
| 9,90 | 33,3 | 1,0072 | 1,0247 | 0,0072 | 0,0247 | 0,7207338 | 13,736 | |||
| -6,50 | 26,8 | 0,9953 | 1,0198 | -0,0047 | 0,0198 | -0,4698229 | 13,835 | |||
| 3,00 | 29,8 | 1,0022 | 1,0221 | 0,0022 | 0,0221 | 0,2178649 | 13,770 | |||
| -2,50 | 27,3 | 0,9982 | 1,0202 | -0,0018 | 0,0202 | -0,1811594 | 13,800 | |||
| 3,70 | 31 | 1,0027 | 1,0230 | 0,0027 | 0,0230 | 0,2686025 | 13,775 | |||