Файл: Реферат Дисциплина Высшая матема т ика Ф. И. О. Абдупаттахов Миржалол Алишерович Город Бекабадский рн, Ташкентская область.doc
Добавлен: 10.01.2024
Просмотров: 32
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»
Письменная работа – реферат
Дисциплина:Высшая математика
Выполнил:
Ф.И.О. Абдупаттахов Миржалол Алишерович
Город: Бекабадский р-н, Ташкентская область
Омск 2021 г.
Содержание
Введение
Распределение Пуассона в теории вероятностей
Числовые характеристики положения о распределении Пуассона
Числовые характеристики разброса
Асимметрия и эксцесс распределения Пуассона
Дополнительные характеристики распределения Пуассона
Распределение Пуассона в математической статистике
Примеры из практики
Заключение
Список использованной литературы
Введение
Теория вероятностей – это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.
История теории вероятности восходит к XVII веку, когда были предприняты первые попытки систематического исследования задач, относящихся к массовым случайным явлениям, и появился соответствующий математический аппарат. С тех пор, многие основы были разработаны и углублены до нынешних понятий, были открыты другие важные законы и закономерности. Множество ученых работало и работает над проблемами теории вероятностей.
Среди них нельзя не обратить внимание на труды Симеона Дени Пуассона ((1781–1840) – французский математик), доказавшего более общую, чем у Якова Бернулли, форму закона больших чисел, а также впервые применившего теорию вероятностей к задачам стрельбы. С именем Пуассона связан один из законов распределения, играющий большую роль в теории вероятностей и ее приложениях.
Число наступлений определённого случайного события за единицу времени, когда факт наступления этого события в данном эксперименте не зависят от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, и не влияет на будущее. А испытания производятся в стационарных условиях, то для описания распределения такой случайной величины обычно используют закон Пуассона (данное распределение впервые предложено и опубликовано этим учёным в 1837 г.).
Этот закон можно также описывать как предельный случай биноминального распределения, когда вероятность p осуществления интересующего нас события в единичном эксперименте очень мала, но число экспериментов m, производимых в единицу времени, достаточно велико, а именно такое, что в процессе p
0 и m
произведение mp стремится к некоторой положительной постоянной величине 
(т.е. mp
).Поэтому закон Пуассона часто называют также законом редких событий.
Распределение Пуассона в теории вероятностей
Функция и ряд распределения
Распределение Пуассона – это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p – параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
Pm = Cnm · pm · (1 – p)n – m
может быть написан, если положить p = a/n, в виде
или
Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению с n. Произведение
весьма близко к единице. Это же относится к величине
очень близка к e–a. Отсюда получаем формулу:
число Эйлера (2,71…).
,
Для производящей функции
величины 
имеем:
Интегральная функция вероятности распределения равна
Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины, количество телефонных звонков в call-центре или количество обращений к веб-серверу за заданный период времени.
Ряд распределения случайной величины Х, распределенной по закону Пуассона, выглядит следующим образом:
| хm | 0 | 1 | 2 | … | m | … |
| Pm | e-a |  |  | … |  | … |
На рис. 1 представлены многоугольники распределения случайной величины Х по закону Пуассона, соответствующие различным значениям параметра а.
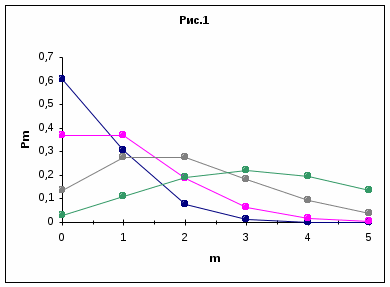
Для начала убедимся, что последовательность вероятностей, может представлять собой ряд распределения, т.е. что сумма всех вероятностей Рm равна единице.
Используем разложение функции ех в ряд Маклорена:
Известно, что этот ряд сходится при любом значении х, поэтому, взяв х=а, получим
следовательно
Числовые характеристики положения о распределении Пуассона
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
По определению, когда дискретная случайная величина принимает счетное множество значений:
Первый член суммы (соответствующий m=0) равен нулю, следовательно, суммирование можно начинать с m=1:
Таким образом, параметр а представляет собой не что иное, как математическое ожидание случайной величины Х.
Кроме математического ожидания, положение случайной величины характеризуется модой и медианой.
Модой случайной величины называется её наиболее вероятное значение.
Для непрерывной величины модой называется точкой локального максимума функции плотности распределения вероятностей. Если многоугольник или кривая распределения имеют один максимум (рис. 2 а), то распределение называется унимодальным, при наличии более одного максимума – мультимодальным (в частности, распределение, имеющее две моды, называется бимодальным). Распределение, имеющее минимум, называется антимодальным (рис. 2 б)
F(x) Pi
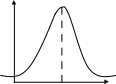
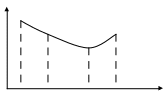
xmod x 0 x
1 x2 x3 x4 x
Наивероятнейшим значением случайной величины называется мода, доставляющая глобальный максимум вероятности для дискретной случайной величины или плотности распределения для непрерывной случайной величины.
Медиана – это такое значение хl, которое делит площадь под графиком плотности вероятности пополам, т.е. медиана является любым корнем уравнения. Математическое ожидание может не существовать, а медиана существует всегда и может быть неоднозначно определенной.
Медианой случайной величины
называется такое её значение = x med, что P ( < x med) = Р ( > x med) =
.Числовые характеристики разброса
Дисперсией случайной величины Х называют математической ожидание квадрата отклонения случайной величины от ее математического ожидания:
Однако, удобнее ее вычислять по формуле:
Поэтому найдем сначала второй начальный момент величины Х:
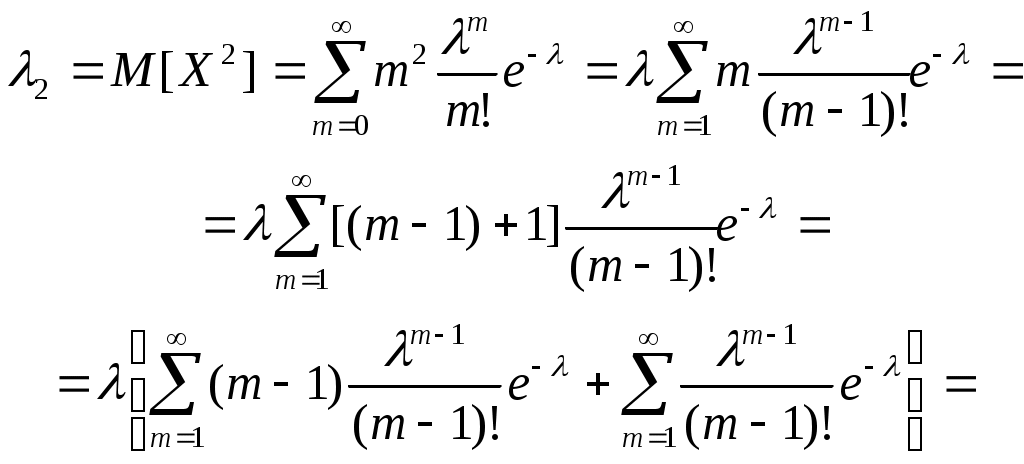
По ранее доказанному
кроме того,
следовательно,
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а.
Это свойство распределения Пуассона часто применяют на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против подобной гипотезы.