Файл: Реферат Дисциплина Высшая матема т ика Ф. И. О. Абдупаттахов Миржалол Алишерович Город Бекабадский рн, Ташкентская область.doc
Добавлен: 10.01.2024
Просмотров: 34
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Найдем вероятность того, что среди n отрезков будет ровно m «занятых». По теореме о повторных независимых испытаниях эта вероятность равна
,
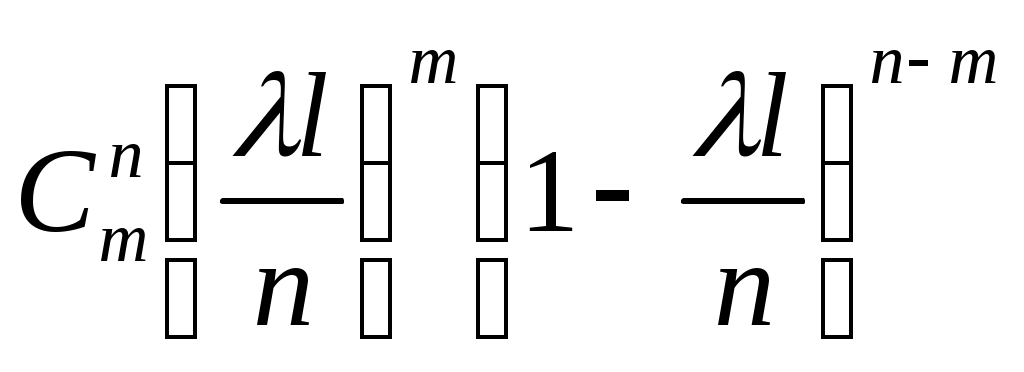или обозначим λl=a:
.
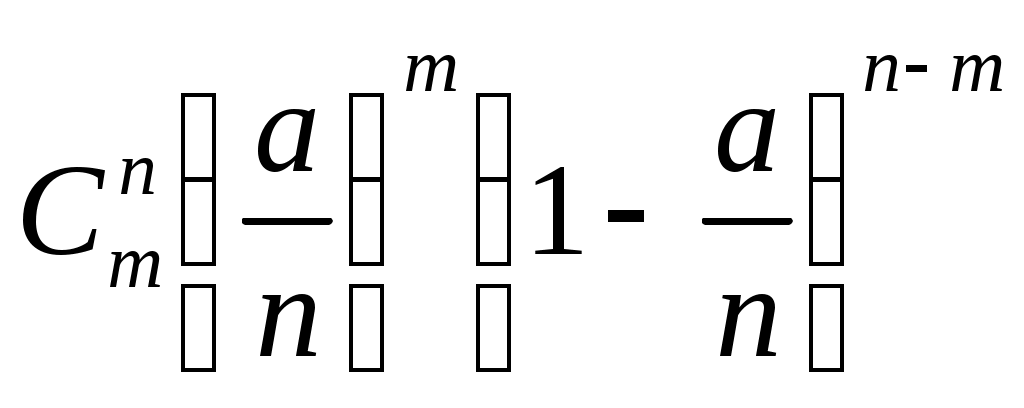При достаточно большом n эта вероятность приближенно равна вероятности попадания на отрезок l ровно m точек, т. к. попадание двух или больше точек на отрезок Δх имеет пренебрежимо малую вероятность. Для того, чтобы найти точное значение Рm, нужно перейти к пределу при n→∞:
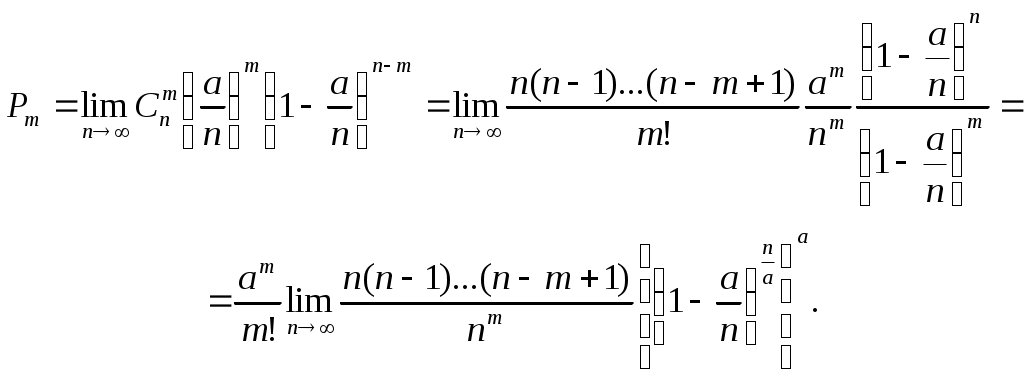
Учитывая, что
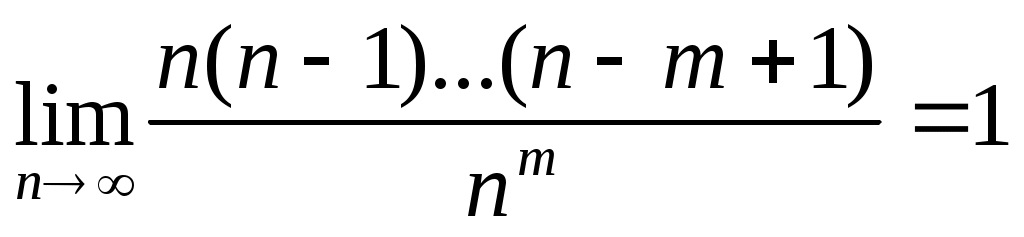
и
,
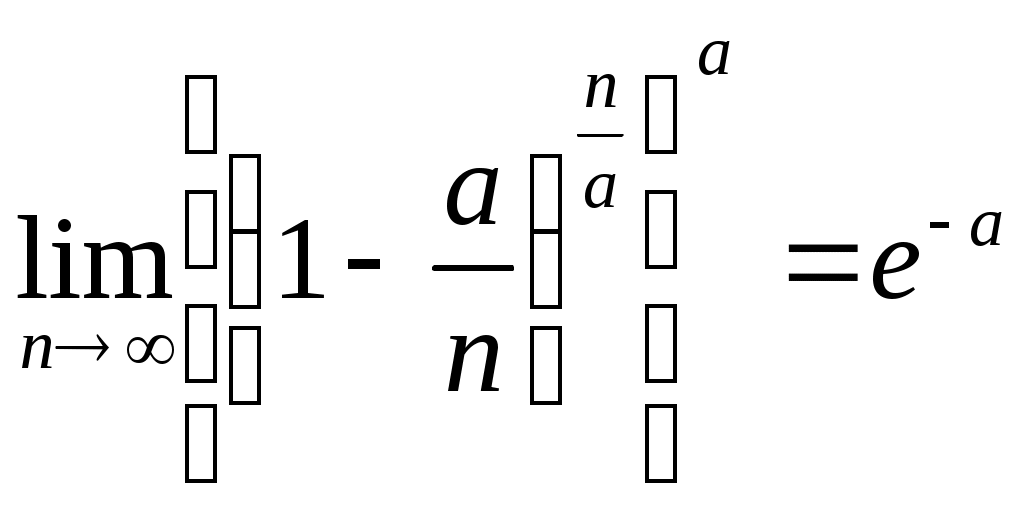получаем, что искомая вероятность выражается формулой
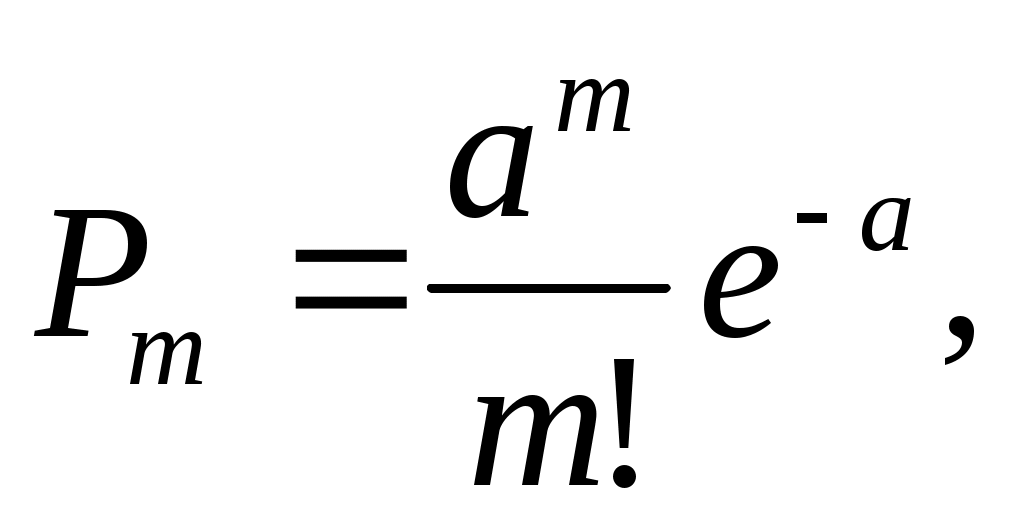
где а=λl, т.е. величина Х распределена по закону Пуассона с параметром а=λl.
Надо отметить, что величина а по смыслу представляет собой среднее число точек, приходящееся на отрезок l.
Величина R1 (вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок l попадет хотя бы одна точка: R1=1-e-a.
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой областью был отрезок l на оси абсцисс. Однако этот вывод легко можно распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
то число точек Х, попавших в любую область D (плоскую или пространственную), распределяется по закону Пуассона:
,
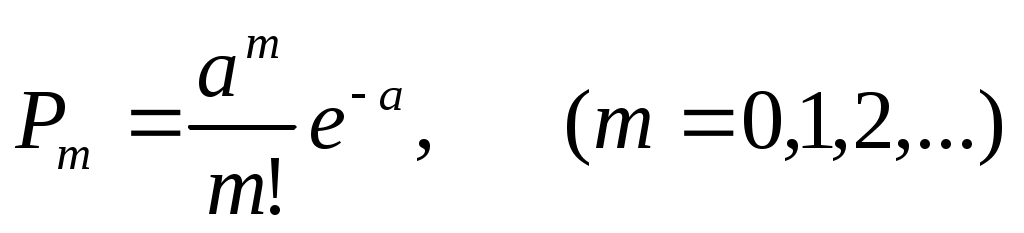
где а – среднее число точек, попадающих в область D.
Для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности (λ=const) несущественно. Если выполнены два других условия, то закон Пуассона все-равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножением плотности λ на длину, площадь или объем, а интегрированием переменной плотности по отрезку, площади или объему.
Примеры из практики
1. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение. Т.к. по условию n=1000 достаточно велико, а m=0,002 мало, можно воспользоваться распределением Пуассона:
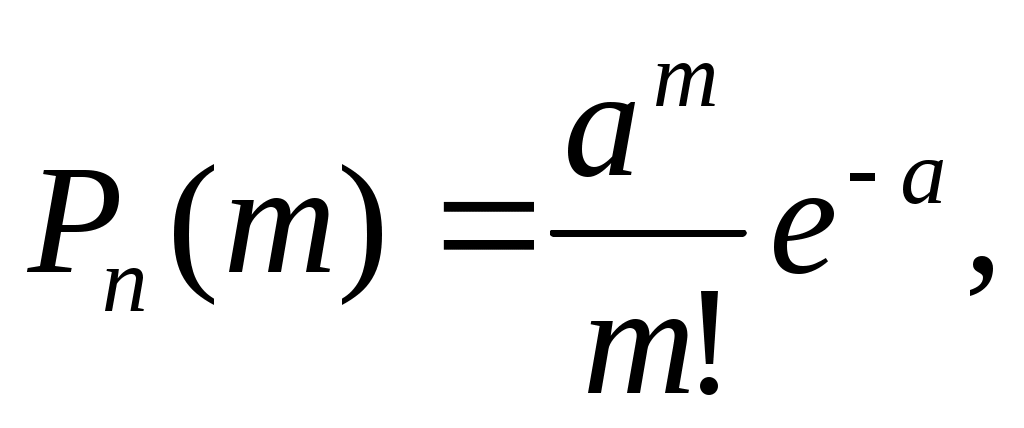
где а=np=1000·0,002=2.
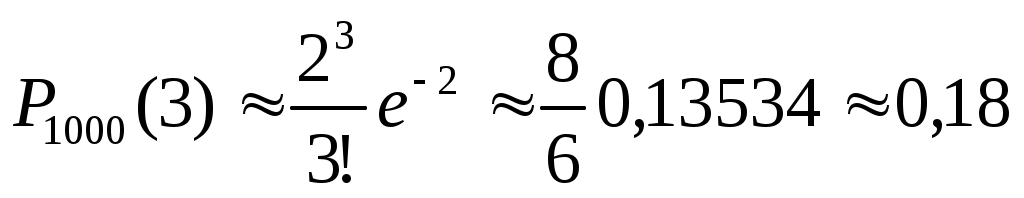
Решение. События «указанный эффект наблюдался по крайней мере один раз» (обозначим через Р) и «указанный эффект не наблюдался ни одного раза» (обозначим через Q), очевидно, являются противоположными. Следовательно, P+Q=1, откуда
Р=1-Q=1-Pn(0)=1-e-a.
По условию Р=0,95, следовательно
е-а=0,05,
а=np=3,
откуда
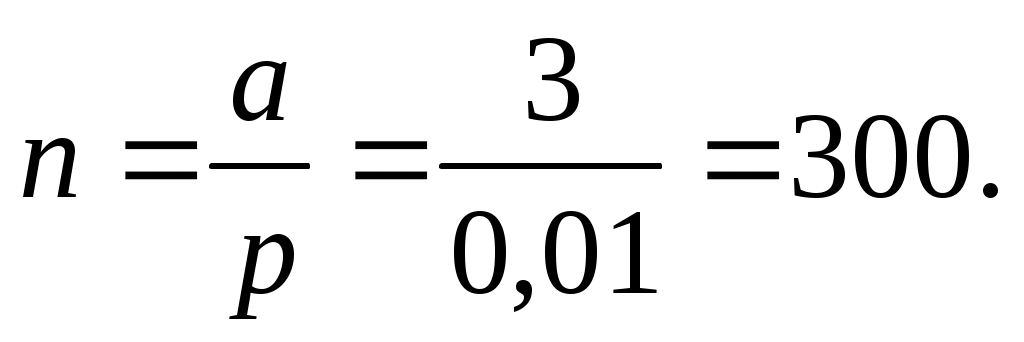
Таким образом, искомое среднее число образцов, которое необходимо испытать, – 300 штук.
Решение. Вероятность выигрыша мала, а число билетов, которое нужно купить, очевидно, велико, поэтому случайное число выигрышных билетов имеет приближенно распределение Пуассона.
События «ни один из купленных билетов не является выигрышным» и «хотя бы один билет – выигрышный» – противоположные. Поэтому сумма вероятностей этих событий равна единице:
Рn(0)+P=1, или Р=1-Рn(0)=1-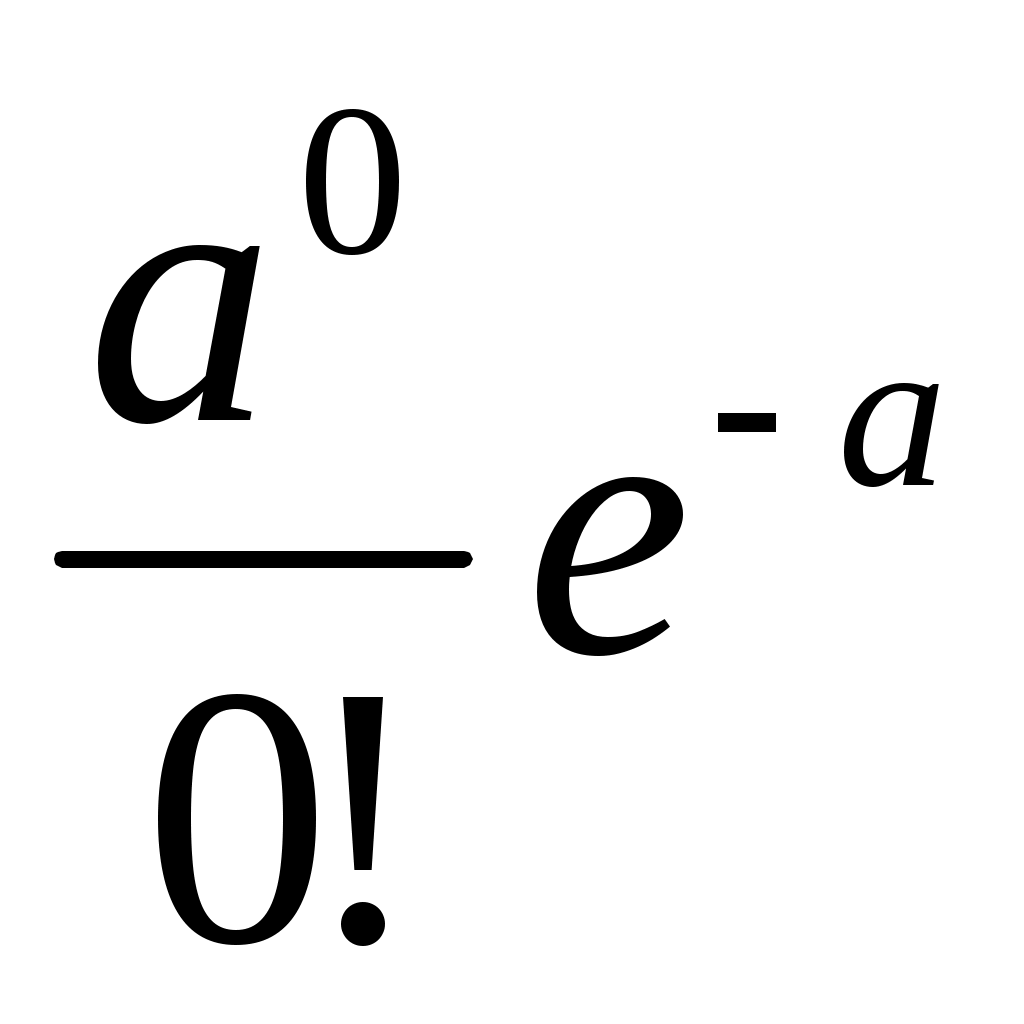
=1-е-а.
По условию, Р≥0,98, или 1-е-а≥0,98. Откуда е-а≤0,02.
По таблице найдем е-3,9=0,02. Т.к. функция е-х – убывающая, предыдущее неравенство выполняется при а≥3,9, или np≥3,9. Отсюда n≥3,9/0,01=390.
Таким образом, надо купить не менее 390 билетов, чтобы выиграть хотя бы по одному из них.
Решение. Среднее число вызовов за две секунды равно:
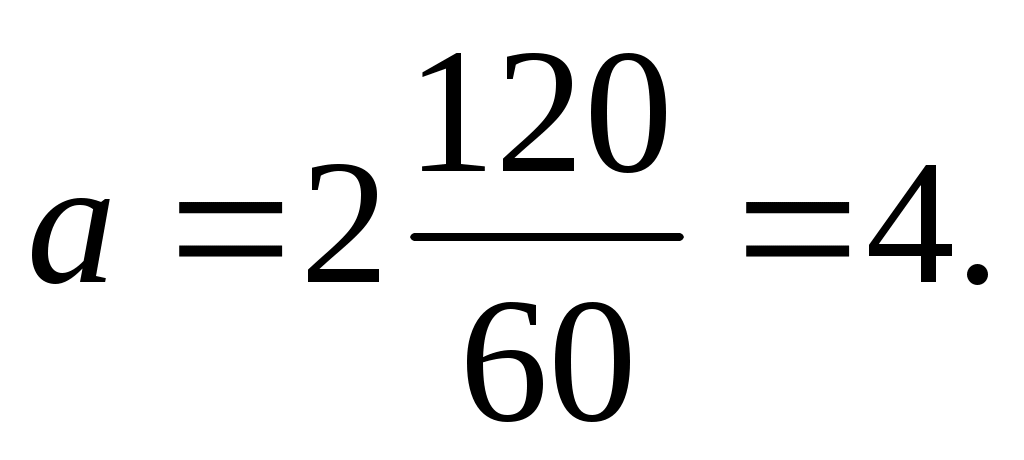
Вероятность того, что на станцию в течение 2-ух секунд не поступит ни одного вызова равна:
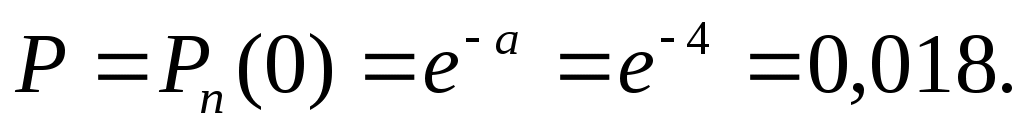
Событие, состоящее в поступлении менее двух вызовов, означает, что на станцию либо не поступило ни одного вызова, либо поступил только один. Таким образом, вероятность поступления менее 2-ух вызовов за то же время равна:
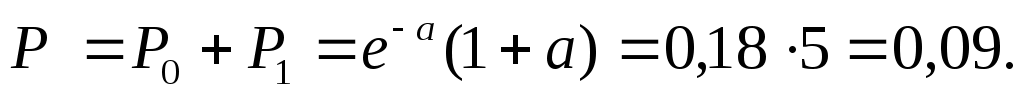
Решение. λ – среднее число электронов, t – время испускания, следовательно,
а=λt.
P=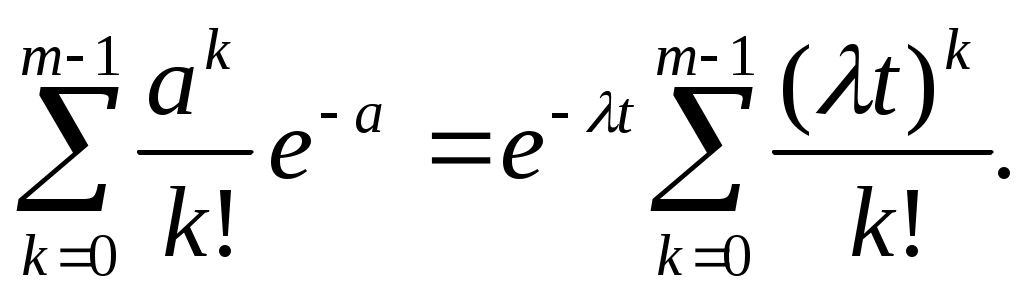
Решение. Находим среднее число электронов а, вылетающих с катода за данный отрезок времени:
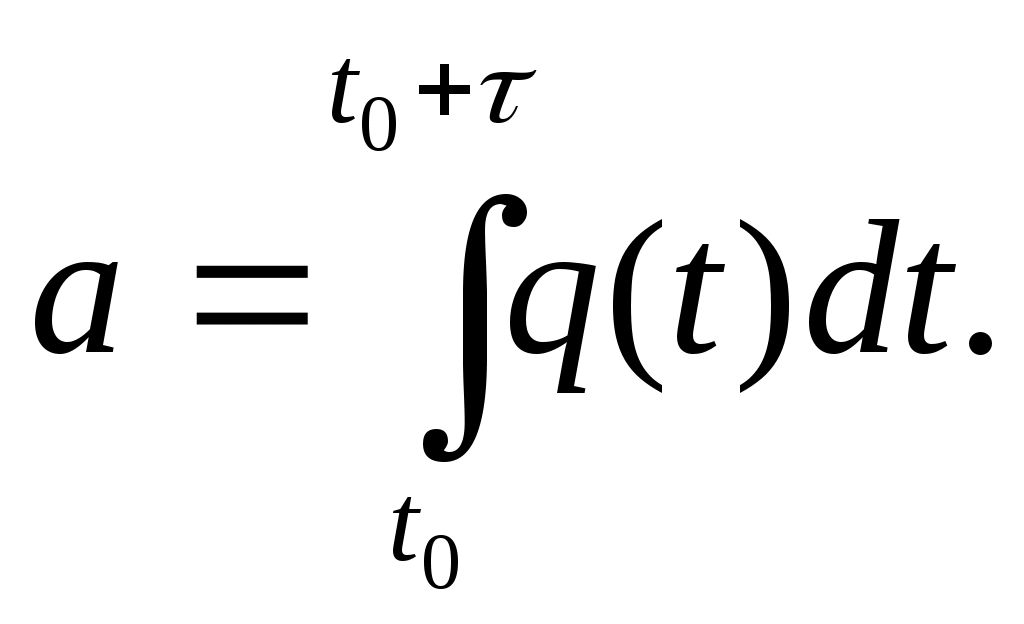
По вычисленному, а определяем искомую вероятность:
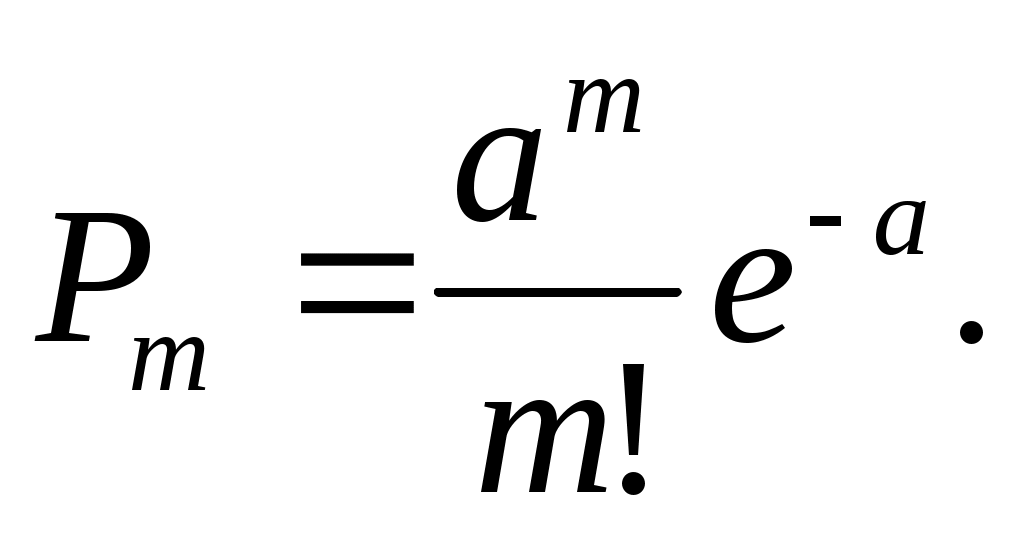
Заключение
В заключение хочется отметить то, что распределение Пуассона является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.
Многие задачи практики сводятся, в конечном счете, к распределению Пуассона. Его особое свойство, заключающееся в равенстве математического ожидания и дисперсии, часто применяют на практике для решения вопроса, распределена случайная величина по закону Пуассона или нет.
Также важен тот факт, что закон Пуассона позволяет находить вероятности события в повторных независимых испытаниях при большом количестве повторов опыта и малой единичной вероятности.
Список использованной литературы
1. Н.Ш. Кремер «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2004.
2. C.А. Айвазян, В.С. Мхитарян «Теория вероятностей и прикладная статистика»: Учеб. пособие. М., 2001.
3. Е.С. Кочетков «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2001.
4. В.А. Фигурин «Теория вероятности и математическая статистика»: Учеб. пособие. – Мн. ООО «Новое знание», 2000.
,или обозначим λl=a:
.При достаточно большом n эта вероятность приближенно равна вероятности попадания на отрезок l ровно m точек, т. к. попадание двух или больше точек на отрезок Δх имеет пренебрежимо малую вероятность. Для того, чтобы найти точное значение Рm, нужно перейти к пределу при n→∞:
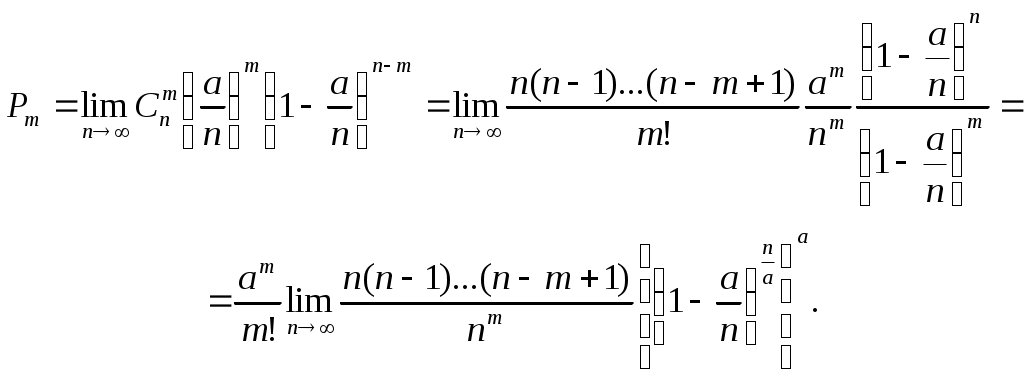
Учитывая, что
и
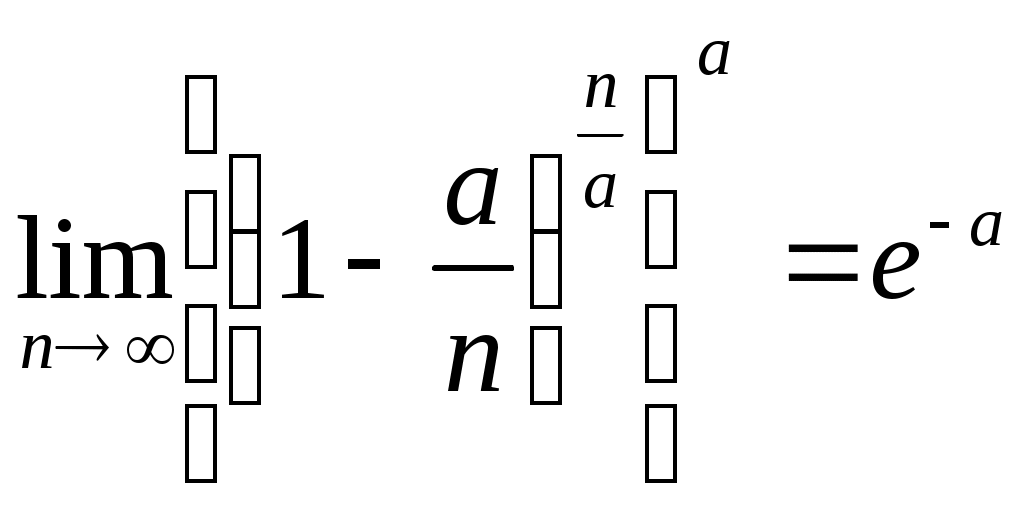,получаем, что искомая вероятность выражается формулой
где а=λl, т.е. величина Х распределена по закону Пуассона с параметром а=λl.
Надо отметить, что величина а по смыслу представляет собой среднее число точек, приходящееся на отрезок l.
Величина R1 (вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок l попадет хотя бы одна точка: R1=1-e-a.
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой областью был отрезок l на оси абсцисс. Однако этот вывод легко можно распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
-
точки распределены в поле статистически равномерно со средней плотностью λ; -
точки попадают в неперекрывающиеся области независимым образом; -
точки появляются поодиночке, а не парами, тройками и т.д.,
то число точек Х, попавших в любую область D (плоскую или пространственную), распределяется по закону Пуассона:
,
где а – среднее число точек, попадающих в область D.
Для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности (λ=const) несущественно. Если выполнены два других условия, то закон Пуассона все-равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножением плотности λ на длину, площадь или объем, а интегрированием переменной плотности по отрезку, площади или объему.
Примеры из практики
1. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение. Т.к. по условию n=1000 достаточно велико, а m=0,002 мало, можно воспользоваться распределением Пуассона:
где а=np=1000·0,002=2.
-
При испытании легированной стали на содержание углерода вероятность того, что в случайно взятой пробе процент углерода превысит допустимый уровень, равна р=0,01. Считая применимым закон редких явлений, вычислить, сколько в среднем необходимо испытать образцов, чтобы с вероятностью р=0,95 указанный эффект наблюдался по крайней мере 1 раз.
Решение. События «указанный эффект наблюдался по крайней мере один раз» (обозначим через Р) и «указанный эффект не наблюдался ни одного раза» (обозначим через Q), очевидно, являются противоположными. Следовательно, P+Q=1, откуда
Р=1-Q=1-Pn(0)=1-e-a.
По условию Р=0,95, следовательно
е-а=0,05,
а=np=3,
откуда
Таким образом, искомое среднее число образцов, которое необходимо испытать, – 300 штук.
-
Вероятность выигрыша по одному лотерейному билету р=0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью Р, не меньшей, чем 0,98?
Решение. Вероятность выигрыша мала, а число билетов, которое нужно купить, очевидно, велико, поэтому случайное число выигрышных билетов имеет приближенно распределение Пуассона.
События «ни один из купленных билетов не является выигрышным» и «хотя бы один билет – выигрышный» – противоположные. Поэтому сумма вероятностей этих событий равна единице:
Рn(0)+P=1, или Р=1-Рn(0)=1-
=1-е-а.По условию, Р≥0,98, или 1-е-а≥0,98. Откуда е-а≤0,02.
По таблице найдем е-3,9=0,02. Т.к. функция е-х – убывающая, предыдущее неравенство выполняется при а≥3,9, или np≥3,9. Отсюда n≥3,9/0,01=390.
Таким образом, надо купить не менее 390 билетов, чтобы выиграть хотя бы по одному из них.
-
Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятность того, что за две секунды на АТС не поступит ни одного вызова; за две секунды на АТС поступит меньше двух вызовов.
Решение. Среднее число вызовов за две секунды равно:
Вероятность того, что на станцию в течение 2-ух секунд не поступит ни одного вызова равна:
Событие, состоящее в поступлении менее двух вызовов, означает, что на станцию либо не поступило ни одного вызова, либо поступил только один. Таким образом, вероятность поступления менее 2-ух вызовов за то же время равна:
-
Случайная величина Х – число электронов, вылетающих с нагретого катода электронной лампы в течение времени t, λ – среднее число электронов, испускаемых в единицу времени. Определить вероятность того, что за время t число испускаемых электронов будет меньше m (mN).
Решение. λ – среднее число электронов, t – время испускания, следовательно,
а=λt.
P=
-
С накаленного катода за единицу времени вылетает в среднем q(t) электронов, где t – время, протекшее с начала опыта. Найти вероятность того, что за промежуток времени длительности τ, начинающийся в момент t0, с катода вылетит ровно m электронов.
Решение. Находим среднее число электронов а, вылетающих с катода за данный отрезок времени:
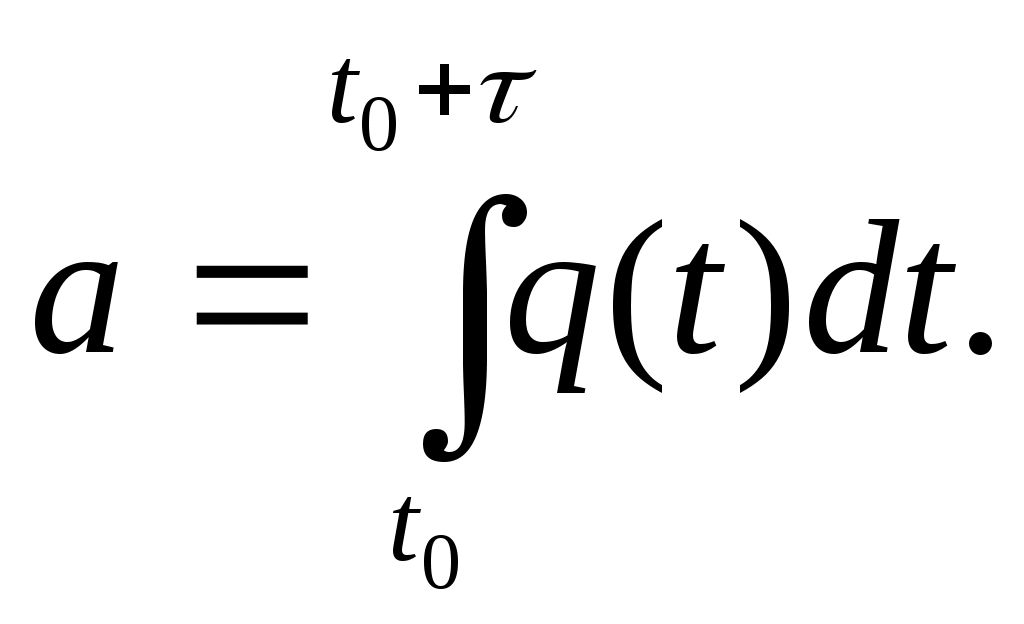
По вычисленному, а определяем искомую вероятность:
Заключение
В заключение хочется отметить то, что распределение Пуассона является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.
Многие задачи практики сводятся, в конечном счете, к распределению Пуассона. Его особое свойство, заключающееся в равенстве математического ожидания и дисперсии, часто применяют на практике для решения вопроса, распределена случайная величина по закону Пуассона или нет.
Также важен тот факт, что закон Пуассона позволяет находить вероятности события в повторных независимых испытаниях при большом количестве повторов опыта и малой единичной вероятности.
Список использованной литературы
1. Н.Ш. Кремер «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2004.
2. C.А. Айвазян, В.С. Мхитарян «Теория вероятностей и прикладная статистика»: Учеб. пособие. М., 2001.
3. Е.С. Кочетков «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2001.
4. В.А. Фигурин «Теория вероятности и математическая статистика»: Учеб. пособие. – Мн. ООО «Новое знание», 2000.
-
Л.П. Трошин «Теория вероятностей», МЭСИ. М.: 2004. -
В.Е. Гмурман «Теория вероятностей и математическая статистика». Учеб. пособие. М.: высшее образование, 2006.