ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 99
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Бланк выполнения задания 5
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все тела и точки механизма.
3. Находятся скорости точек и угловые скорости тел.
4. Находятся ускорения точек и угловые ускорения тел.
5. Показываются на рисунке все векторы скоростей и ускорений.
6. Записывается ответ.
Практическое задание 6
Тема 2.5. Сложное движение точки и твердого тела
Задание
Круглая пластина (рис. 6.1) радиусом 0,1(С + 1) (м) вращается вокруг неподвижной оси, проходящей перпендикулярно рисунку через нижнюю точку О по закону Пt2 – Гt (рад). По окружности пластины движется точка М из точки А. Закон ее относительного движения – длина дуги между точками А и М равна
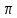 (П + 1)t2 (м). Определите абсолютную скорость и ускорение точки М в момент времени 1 с.
(П + 1)t2 (м). Определите абсолютную скорость и ускорение точки М в момент времени 1 с.
Рис. 6.1
Рекомендации по выполнению задания 6
-
Выделите точку, совершающую сложное движение. -
Проведите анализ движения точки – выделите относительное, переносное, абсолютное движения. -
Изобразите точку на рисунке в заданный момент времени. -
Определите относительную скорость точки:-
Постройте траекторию точки в относительном движении. -
Постройте вектор относительной скорости точки, определите его модуль.
-
-
Определите переносную скорость точки:-
Постройте траекторию точки тела, совпадающей с исследуемой точкой в заданный момент времени в переносном движении точки. -
Постройте вектор переносной скорости точки, определите его модуль.
-
-
Определите абсолютную скорость точки:-
Постройте вектор абсолютной скорости точки либо по касательной к траектории в абсолютном движении, либо как диагональ параллелограмма, построенного на векторах относительной скорости точки и переносной скорости точки. -
Определите модуль либо по теореме Пифагора, либо по теореме косинусов.
-
-
Определите относительное ускорение точки:-
Постройте траекторию точки в относительном движении. -
Постройте вектор относительного ускорения точки, определите его модуль.
-
-
Определите переносное ускорение точки:-
Постройте траекторию точки тела, совпадающей с исследуемой точкой в заданный момент времени в переносном движении. -
Постройте вектор переносного ускорения точки, определите его модуль.
-
-
Определите абсолютное ускорение точки:-
Постройте вектор абсолютного ускорения точки как геометрической суммы трех ускорений – относительного, переносного и поворотного. -
Определите модуль абсолютного ускорения точки.
-
Бланк выполнения задания 6
1. Записываются данные задания.
2. Представляется рисунок, на котором показана точка, совершающая сложное движение на теле, в заданный момент времени.
3. Находятся все скорости точки.
4. Находятся все ускорения точки.
5. На рисунке показываются все векторы скоростей и ускорений точки.
6. Записывается ответ.
Практическое задание 7
Тема 3.1. Динамика материальной точки
Задание
Материальная точка массой Г + 1 (кг) движется в горизонтальной плоскости ХОY системы координат под действием силы F̅, где ее проекция на ось Х равна (C + 800)sin(Гt) (Н), а на ось Y равна (900 – П)cos(Гt) (Н). Определите уравнение движения точки при следующих начальных условиях: начальная абсцисса равна П + 2 (м); начальная ордината равна Г + 1 (м); проекция вектора начальной скорости на ось Х равна С – 6 (м/с); проекция вектора начальной скорости на ось Y равна 0 (м/с).
Рекомендации по выполнению задания 7
-
Выделите материальную точку, движение которой рассматривается. -
Расставьте внешние силы, действующие на материальную точку. -
Выделите тела связей с их реакциями. -
Постройте систему координат. -
Составьте дифференциальные уравнения абсолютного движения материальной точки. -
Решите дифференциальные уравнения абсолютного движения материальной точки.
Бланк выполнения задания 7
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все силы.
3. Записываются уравнения динамики материальной точки.
4. Решаются уравнения динамики материальной точки.
5. Записывается ответ.
Практическое задание 8
Тема 3.3. Основные теоремы динамики механической системы
Задание
Круглая пластина (рис. 8.1) радиусом 0,3(Г + 1) (м) и массой C + 30 (кг) вращается с угловой скоростью (С – 20) (с–1) вокруг вертикальной оси Z, проходящей через точку О перпендикулярно рисунку.
На пластине имеется желоб, по которому начинает двигаться точка М массой П + 2 (кг) из точки А по закону 0,1(Г + 3)t2 (м).
Найдите угловую скорость пластины в момент времени 1 с.
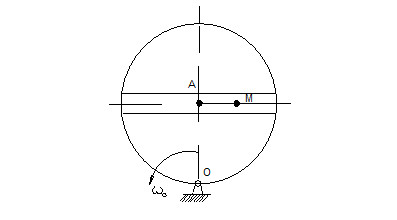
Рис. 8.1
Рекомендации по выполнению задания 8
-
Выделите твердое тело и материальную точку.
Рассмотрите их совместное движение.
Расставьте внешние силы, действующие на тело и материальную точку.
-
Выделите тела связей.
Освободите тело от существующих связей, их действие замените реакциями связей.
-
Покажите векторы скоростей и найдите центр тяжести тела. -
Постройте систему координат. -
Составьте уравнение, применяя одну из основных теорем динамики механической системы.
Решите полученное уравнение, определите неизвестную по условию величину.
Бланк выполнения задания 8
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все силы и скорости.
3. Записывается уравнение теоремы об изменении кинетического момента механической системы.
4. Решается уравнение.
5. Записывается ответ.
Практическое задание 9
Тема 3.3. Основные теоремы динамики механической системы
Задание
Механическая система в вертикальной плоскости (рис. 9.1) состоит из груза 1, ступенчатых шкивов 2 и 3 и катка 4 с радиусами: r2 = 0,2 (м); R2 = 0,4 (м); г3 = 0,3 (м); R3 = 0,4 (м); R4 = 0,5 (м). Радиусы инерции 2-го и 3-го тел: i2 = 0,3 (м); i3 = 0,33 (м). Коэффициент трения скольжения груза 1 о плоскость равен 0,1; коэффициент трения качения колеса 4 равен 0,002 (м). Система начинает движение из состояния покоя в направлении заданной силы F1, которая равна C + 1 (кН) (если П = 0… 2), или в направлении, обусловленном направлением вращения моментов M2, который равен C + 2 (кН·м) (если П = 3...5); М3, который равен С + 3 (кН·м) (если П = 6... 7), и М4, который равен С + 4 (кН·м) (если П = 8... 9). Определите скорость груза 1 в тот момент, когда его перемещение станет равным 0,1(Г + 1) (м), если массы тел следующие: масса первого тела Г + 2 (кг); второго 2Г + 1 (кг); третьего П + 2 (кг); четвертого ПГ + 1 (кг); углы: α равен 30 + 5П (град); β равен 80 – 5П (град).
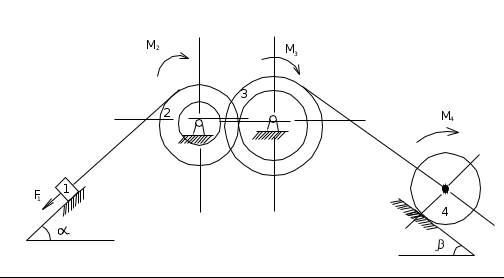
Рис. 9.1
Рекомендации по выполнению задания 9
-
Выделите твердое тело или систему тел, движение которых рассматривается.
Расставьте внешние силы, действующие на тело или систему тел.
-
Выделите тела связей.
Освободите тело от существующих связей, их действие замените реакциями связей.
-
Покажите векторы скоростей и найдите центр тяжести тела. -
Постройте систему координат. -
Составьте уравнение, применяя одну из основных теорем динамики механической системы.
Решите полученное уравнение, определите неизвестную по условию величину.
Бланк выполнения задания 9
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все силы.
3. Записывается уравнение теоремы об изменении кинетической энергии механической системы.
4. Решается уравнение.
5. Записывается ответ.
Практическое задание 10
Тема 3.5. Динамика твердого тела и принцип Даламбера
Задание
Вал (рис. 10.1), закрепленный вертикально в подпятнике А и в подшипнике В, вращается с постоянной угловой скоростью С + 10 (c–1).
С валом в одной плоскости под углами α, равным 45 + 5Г (град), и β, равным 90 – 5П (град), к его оси жестко соединены однородный стержень CD длиной Г + 1 (м), массой П + 2 (кг) и невесомый стержень ЕМ длиной П + 3 (м), на конце которого закреплена материальная точка М массой Г + 4 (кг). Определите реакции в точках А и В, если |AС|=|CE|=|EB| и равны 0,5(Г+1) (м).
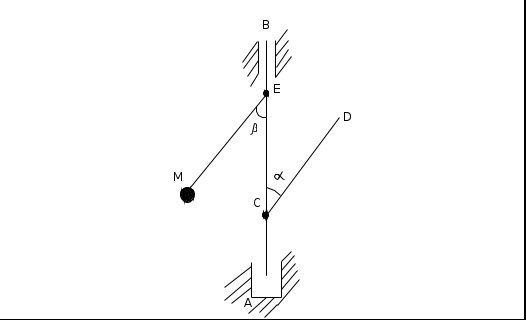
Рис. 10.1
Рекомендации по выполнению задания 10
-
Выделите тело и материальную точку.
Рассмотрите их совместное движение.
Расставьте внешние силы, действующие на тело и материальную точку.
2. Выделите тела связей.
Освободите твердое тело от связей, их действие замените реакциями связей.
3. Покажите и найдите центр тяжести тела.
Покажите и найдите силу тяжести тела.
4. Постройте систему координат.
5. Найдите и покажите силы инерции.
6. Примените принцип Даламбера, записывая уравнения динамического равновесия.
Решите полученную систему уравнений и определите неизвестные величины.
Бланк выполнения задания 10
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все активные силы и силы реакции.
-
Находятся все ускорения и силы инерции.
4. Записывается принцип Даламбера в виде уравнений динамического равновесия.
5. Решаются полученные уравнения.
6. Записывается ответ.
Практическое задание 11
Тема 3.6. Принцип возможных перемещений и общее уравнение динамики точки
Задание
Рис. 11.1
Многозвенный механизм (рис. 11.1), расположенный в горизонтальной плоскости ХОY, находится в равновесии. Определите значение силы Р, если сила F1 равна С + 1 (кН); сила F2 равна С + П (кН); сила F3 равна C + Г (кН); момент М1 равен П + Г (кН·м); момент М2 равен С – П + Г (кН·м); угол α равен 45 + 5П (град); угол β равен 90 – 5П (град); угол χ равен 20 + 5П (град); |О1A|=|AB|=|BC|=|BD|= 1 м. Точка В находится между точками А и С.
Рекомендации по выполнению задания 11
-
Выделите точки механической системы, к которым приложены внешние силы.
Проведите анализ возможного движения точек и тел механической системы под действием сил.
2. Изобразите на рисунке точки механической системы, к которым приложены силы.
3. Определите возможные перемещения всех точек и тел механической системы.
Постройте векторы возможных перемещений точек по касательной к траектории.
-
Примените в виде уравнения принцип возможных перемещений. -
Решите полученное уравнение и найдите неизвестную по заданию величину.
Бланк выполнения задания 11
1. Записываются данные задания.
2. Представляется рисунок, на котором показаны все силы.
3. Находятся возможные перемещения точек.
4. Записывается принцип возможных перемещений.
5. Решается полученное уравнение.
-
Записывается ответ.
Практическое задание 12
Тема 3.6. Принцип возможных перемещений и общее уравнение динамики точки
Задание
Круглое однородное колесо радиусом 0,1(Г + 1) (м) и массой (П + 2) (кг) катится по неподвижной горизонтальной оси без скольжения из состояния покоя.
К центру колеса приложена постоянная горизонтальная сила (С + П) в Ньютонах.
Коэффициент трения качения равен 0,001 (м).
Определите абсолютное ускорение центра колеса, решив задачу с помощью общего уравнения динамики.