Файл: Отчет по практической работе 1 Вариант 25 по дисциплине Метрология, стандартизация и сертификация.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение
высшего образования «Южно-Уральский государственный университет»
(национальный исследовательский университет)

Высшая школа электроники и компьютерных наук

Кафедра «Информационно-измерительная техника»

Обработка и формы представления результата прямых измерений с многократными наблюдениями

ОТЧЕТ

по практической работе №1

Вариант №25

по дисциплине «Метрология, стандартизация и сертификация»

Выполнил:

студент группы П–273

/ М.П. Ходырев /

(подпись)

«» г.

Проверил: ст. преподаватель

/ И.С. Никитин /

(подпись)

«» г.

Проведено измерение ЭДС с помощью потенциометра постоянного тока. Результаты наблюдений приведены в таблице 1. Определите результат измерения напряжения. Уровень значимости q принять равным 0,01

Исходные данные для выполнения практической работы согласно варианту №25

Показания потенциометра, В
3,73094	0,671632
3,75549	0,672226
3,68536	0,670530
3,72568	0,671505
3,73585	0,671751
3,68354	0,670486
3,74574	0,671990
3,74597	0,671996
3,65684	0,669840
3,73597	0,671754
3,69597	0,670786
3,71542	0,671257
3,75586	0,672235
3,71515	0,671250
3,72548	0,671500
3,74694	0,672019
3,71511	0,671249
3,72814	0,671564
3,74593	0,671995
3,71299	0,671198

---

Алгоритм задания исходных данных для практической работы:

,



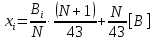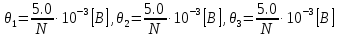
где N – порядковый номер студента в общем списке группы;

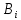– исходные данные для выполнения практической работы, взятые из таблицы 1;

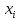– исходные данные для выполнения практической работы, взятые из таблицы для варианта N;

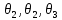– составляющие систематической погрешности.

,



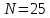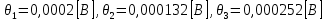
Уровень значимости q=1%

Проверка наличия в результатах измерений грубых погрешностей и исключение их при необходимости

Согласно ГОСТ 8.736-2011 для исключения грубых погрешностей следует использовать критерий Граббса. Исследование проводится в 2 этапа: проверка гипотезы о том, что наибольший x_max результат измерения вызван грубыми погрешностями; проверка гипотезы о том, что наименьший x_min результат измерений вызван грубыми погрешностями.

Каждое исследование проводится согласно приведенному ранее порядку.

Исследование x_max

1. 
   Формирование исходных данных.
   

Исходные данные для исследования представлены в таблице 1.

2. 
   Формулировка нулевой (H₀) и альтернативной (H₁) гипотез.
   

Гипотеза H₀— наибольший x_max результат измерения вызван грубыми погрешностями;

---

Гипотеза H₁ — наибольший x_max результат измерения не содержит грубой погрешности (промаха).

3. 
   Выбор вида статистической проверки гипотезы.
   

Для исследования результатов измерений на наличие систематических погрешностей будет использован критерий Граббса.

4. 
   Определение уровня значимости.
   

Уровень значимости q согласно заданию равен 0,01 (1%).

5. 
   Вычисление фактического значения выбранного статистического критерия на основе исходных данных.
   

Согласно критерию Граббса критическое значение определяется по формул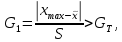е где: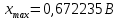







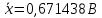
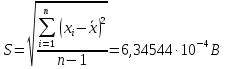
Тогда:

6. 
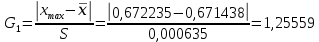
   Нахождение в таблицах квантиля распределения.
   

Согласно таблице A.1 приложения А при уровне значимости q и объеме выборки n квантиль G_T (q, п) будет равен:

7. 
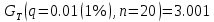
   Проверка, выполняется ли указанное в выбранном критерии условие. Согласно критерию Граббса, наибольший x_max результат измерений вызван грубыми погрешностями если выполняется неравенство:
   

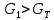
где G_T—теоретическое значение критерия Граббса при выбранном уровне значимости q и числу измерений

---

n в группе.

При подстановке значений данное неравенство принимает вид: 1,25559 > 3,001.

8. 
   Формулировка вывода.
   

Видно, что условие не выполняется, следовательно,

отвергается нулевая и принимается альтернативная гипотеза.

Вывод: условие критерия Граббса не выполняется, следовательно, отвергается нулевая гипотеза (H₀) и принимается альтернативная гипотеза (H₁), согласно которой наибольший x_max результат измерения не вызван грубыми погрешностями.

Исследование x_min

1. 
   Формирование исходных данных.
   

Исходные данные для исследования представлены в таблице 1.

2. 
   Формулировка нулевой (H₀) и альтернативной (H₁) гипотез.
   

Гипотеза H₀ — наименьший x_min результат измерения вызван грубыми погрешностями;

Гипотеза H₁ — наибольший x_min результат измерения не содержит грубой погрешности (промаха).

3. 
   Выбор вида статистической проверки гипотезы.
   

Для исследования результатов измерений на наличие систематических погрешностей будет использован критерий Граббса.

4. 
   Определение уровня значимости.
   

Уровень значимости q согласно заданию равен 0,01 (1%).

5. 
   Вычисление фактического значения выбранного статистического критерия на основе исходных данных.
   

Согласно критерию Граббса критическое значение определяется по формуле

---

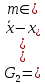
где:







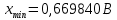
Тогда:

6. 
   Нахождение в таблицах квантиля распределения.
   

Согласно таблице A.1 приложения А при уровне значимости q и объеме выборки n квантиль G_T (q, п) будет равен:

7. 
   Проверка, выполняется ли указанное в выбранном критерии условие. Согласно критерию Граббса, наибольший x_min результат измерений вызван грубыми погрешностями если выполняется неравенство:
   

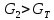
где G_T—теоретическое значение критерия Граббса при выбранном уровне значимости q и числу измерений n в группе.

При подстановке значений данное неравенство принимает вид: 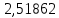> 3,001.

8. 
   Формулировка вывода.
   

Видно, что условие 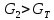не выполняется, следовательно,

отвергается нулевая и принимается альтернативная гипотеза.

Вывод: условие критерия Граббса не выполняется, следовательно, отвергается нулевая гипотеза (H₀) и принимается альтернативная гипотеза (H₁), согласно которой наибольший x_min результат измерения не вызван грубыми погрешностями.

Итоговыйвывод: поскольку условие критерия Граббса не выполняется в обоих случаях, ни наибольший x_max, ни наименьший x_min результат измерения не вызваны грубыми погрешностями (не содержит промаха).

---