ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 118
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
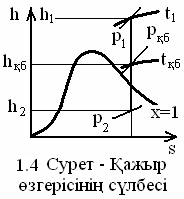
1 = 3302 кДж/кг, hқб = 2538 кДж/кг, h2 = 2092 кДж/кг, h’қб = 439,4 кДж/кг, h’2 = 121,4 кДж/кг, t’’2 = 29 0C, t’қб = 104,8 0C (1.3 пен 1.4 суреттерді қараңыз).
Қайрылған будың үлесін жылылық теңестігінен, араластырғышта қорек суы рқб -дағы қанығу ыстықтығы t’қб-ға дейін қыздырылады деп, анықтаймыз
 (1.35)
(1.35)
Мұндағы (кДж/кг) hқб - шығырдың алуындағы будың қажыры;
h’қб мен h’2 – рқб мен р2–лердегі қаныққан шықтардың қажырлары.
Жаңғыртулы айналымдағы 1 кг будың пайдалы жұмысы

 (1.36)
(1.36)
Бу мен жылылықтың меншікті шығындары
 (1.37)
(1.37)
 (1.38)
(1.38)
Қайрылған жылылықты Ренкин айналымының қайтымды ПЖЕ-сі
 (1.39)
(1.39)
Қайрылған жылылығы жоқ Ренкин айналымының қайтымды ПЖЕ-сі
 (1.40)
(1.40)
Қайрылған жылылықтың әсері
 (1.41)
(1.41)
Бақылау сұрақтары
2 Жылуөткізгіштік пен жылуөту
m=1 n=5
2.1 Тапсырма. Денелердің жылуөткізгіштік еселеуішін тікмегзем
әдісімен анықтау
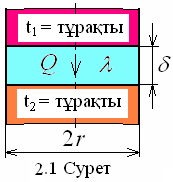
Жылуөткізгіштігі анықталатын дене өресі r =10 мм мен қалыңдығы δ = 1 мм-лі сырықты табақшадан жасалған. Ол ыстықтықтары t1 = 120 + m + 0,2n=122 0C мен t2 = 20 + m + 0,2n=22 0C тұрақты, қалыптасқан жылулық ағыны Q = 23,2 Вт, екі үйектің арасында тығыз орналасқан. Зерттелетін дене өрелі жылулық ысыраптары болмастай өтеуленген (2.1 суретті қараңыз).
Зерттелген дененің жылуөткізгіштік λ еселеуішін анықтаңыз.
2.1 Тапсырма шешімі (m =1 n = 5).
Зерттелген дененің жылуөткізгіштік λ еселеуішін қалыптасқан жылы-лықтың кейіптемесімен табамыз

(2.1)
 (2.2)
(2.2)
m =1 n = 5 түрлемінің жауабы λ ═ 0,739 Вт/(м∙К).
Бақылау сұрақтары
1. Жылуөткізгіштік еселеуіштің анықтаушы ыстықтығы не болады?
2. Жылуөткізгіштік еселеуішті ыстықтыққа тәуелді қалай анықталады?
3. Нақты жағдайлардағы есептің әдісі қандай болады?
4. Неліктен зерттелетін дененің мөлшерлері δ << r болуға тиіс?
5. Денелердің жылуфизикалық қасиеттерін зерттеу неліктен маңызды?
2.2 Тапсырма. Жылуөту
m=1 n=5
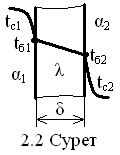
Пештің шамот кірпішінен жасалған қабырғасының жылуөткізгіштік еселеуіші Вт/(м·К) мен қалыңдығы
Вт/(м·К) мен қалыңдығы  . Пештегі газ бен бөлмедегі ауаның ыстықтықтары
. Пештегі газ бен бөлмедегі ауаның ыстықтықтары  мен
мен  Газдан қабырғаға және қабырғадан ауаға берілетін жылудың еселеуіштері
Газдан қабырғаға және қабырғадан ауаға берілетін жылудың еселеуіштері  мен
мен  (2.2 суретті қараңыз).
(2.2 суретті қараңыз).
Жылуөту еселеуіші k, Вт/(м2·К) мен жылу ағынының тығыздығы q, Вт/м2 және қабырғаның tб1 мен tб2 бет ыстықтықтарын дәлдігі 5 пайыз жуықты әдіспен анықтаңыз.
2.2 Тапсырма шешімі (m =1 n = 5).
Төрт белгісіздерді анықтау үшін келесі кейіптемелерді аламыз
 (2.3)
(2.3)
 (2.4)
(2.4)
 (2.5)
(2.5)
 (2.6)
(2.6)
Пештің қабырғасының жылуөткізгіштік еселеуішінің ыстықтыққа сызықты тәуелділігі арқылы оның (2.4)-тегі аумаққылық орта мәні белгілі шекті мәндерінің арифметикалық орта мәніне тең екенін көреміз
 (2.7)
(2.7)
Белгісіз tб1 мен tб2-лермен анықталатын (2.7)-дегі λ1 мен λ2-лер де белгісіз болады. Сондықтан λор – бесінші белгісіз шама. Жылуөту еселеуіші
 (2.8)
(2.8)
(1.3) ÷ (1.5)-терден шығатынынан, мұнда бесінші тәуелсіз теңдеу болмайды.
Сонымен, (1.3) ÷ (1.6) теңдеулердің жүйесі тұйықталмайтындықтан, есепті біртіндеп жуықтау әдісімен (БЖӘ) шешеміз.
БЖӘ-нің бірінші жуықтысы ретінде қабырғаның орта ыстықтығы деп оны қоршаған жылутасығыштар ыстықтықтарының арифметикалық орта мәнін аламыз tбор' ≈ (1200 + 30)/2 = 650 0С. Анықталатын жылуөткізгіштік пен жылуөту еселеуіштері және жылу ағынының тығыздығы мен қабырғаның бет ыстықтықтарының бұған сәйкесті бірінші жуықты мәндерін табамыз
λор'═0,84(1+0,695∙10-3∙612)═1,219 Вт/(м∙К), (2.7')

 (2.8')
(2.8')
q' = k'(tс1 – tс2) = 2,974(1194 - 30) =3461,736 Вт/м2, (2.6')
tc1' = tс1 – q'/α1 =1194 – 3461,736/32 = 1085,82 0С, (2.3')
tc2' = tс2 + q'/α2 = 32 + 3461,736/10 = 376,173 0С. (2.5')
БЖӘ-нің екінші жуықтысы ретінде қабырғаның орта ыстықтығы деп оның бірінші жуықтысындағы бет ыстықтықтарының арифметикалық орта мәнін алып, бұған сәйкесті жылуөткізгіштік пен жылуөту еселеуіштері және жылу ағыны тығыздығының (екінші жуықты) мәндерін табамыз
tбор" ≈ (tб1' + tб2')/2 ═ (1085,82 + 376,173)/2 ═ 725 0С, (2.9")
λор"═0,84(1+0,695∙10-3∙730,996)═1,2667 Вт/(м∙К), (2.7")

 (2.8")
(2.8")
q" = k"(tс1 – tс2) = 3,044(1194 - 30) =3543,216 Вт/м2. (2.6")
Жылу ағыны тығыздығының бұл мәніндегі қабырғаның бет ыстықтықтары мен қабырғаның орта ыстықтығы және бұған сәйкесті жылуөткізгіштік еселеуішінің үшінші жуықтаудағы орта мәні келесіге тең
tб1" = tс1 – q"/α1 =1194 – 3543,216/32 = 1083,2745 0С, (2.3")
tб2" = tс2 + 21/α2 = 30 + 3543,216/10 = 384,3216 0С, (2.5")
tбор"' ≈ (tб1" + tб2")/2 ═ (1083,2745 + 384,3216)/2 ═ 733,798
0С, (2.9"')
λор"'═0,84(1+0,695∙10-3∙733,798)═1,268 Вт/(м∙К). (2.7"')
Үшінші жуықтыда жылуөткізгіштік еселеуішінің орта мәні онша өзгерген жоқ, яғни, оның есептік дәлділігі берілгенінен келесідей көп жоғары
 (2.9)
(2.9)
Сонымен, есеп аяқталады. Оның m =1 n = 2 түрлемінің жауабы ретінде бұл жолы екінші жуықты қорытындылары алынады
tб1 ≈ tб1" = 1083,2745 0С, tб2 ≈ tб2" = 383 0С, k ≈ k" ═ 3,044 Вт/(м2·К), q≈q"=3543,216 Вт/м2.
Кейде талдаулық күрделі шешімдердің орнына мүмкін дәлдікпен БЖӘ-ні пайдаланған ұтымды.
Бақылау сұрақтары
1. Пештің жылылық ысыраптарын қалай бағалап, азайтуға болады?
2. Пештің ішкі бетінің күйеленуі жылулық неге соғады?
3. Қабырғаның бет ыстықтықтары қалай тұрақталады?
4. α1, α2, k-лердің мәндерін өзара салыстырыңыздар.
5. 2.2 суреттегі ыстықтықтар α1, λ/δ, α2, k-лерге қалай байланысты?
6. БЖӘ-нің қаралған есептегі пайдалануын түсіндіріңіздер.
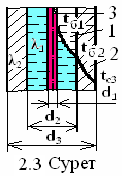 2.3 Тапсырма. Сұйықтың жылуөткізгіштік
2.3 Тапсырма. Сұйықтың жылуөткізгіштік
еселеуішін қыздырылған сым әдісімен анықтау
m=1 n=5
Сұйықтардың жылуөткізгіштік еселеуішін «қыз-дырылған сым» әдісімен анықтайтын аспапта (2.3 суретті қараңыз) платина сымы 3 пен кварц 2 түтікшенің аралығына май 1 құйылған. Платина сымының қосөресі мен ұзындығы d1 = 0,12 мм мен l = 90 мм; кварц түтікшенің ішкі және сыртқы қосөрелері d2 = 1 мм мен d3 = 3 мм және жылуөткізгіштік еселеуіші λ2 ═ 1,4 Вт/(м·К).
Жылулық ағыны Q = 1,8 + 0,1m + 0,02n=2 Вт пен платина сымының ыстықтығы tб1 = 106,9 + m + 0,2n=108,9 0C және кварц түтікшенің сыртқы бет ыстықтығы t
Қайрылған будың үлесін жылылық теңестігінен, араластырғышта қорек суы рқб -дағы қанығу ыстықтығы t’қб-ға дейін қыздырылады деп, анықтаймыз

 (1.35)
(1.35)Мұндағы (кДж/кг) hқб - шығырдың алуындағы будың қажыры;
h’қб мен h’2 – рқб мен р2–лердегі қаныққан шықтардың қажырлары.
Жаңғыртулы айналымдағы 1 кг будың пайдалы жұмысы
Бу мен жылылықтың меншікті шығындары
 (1.37)
(1.37)Қайрылған жылылықты Ренкин айналымының қайтымды ПЖЕ-сі
 (1.39)
(1.39)Қайрылған жылылығы жоқ Ренкин айналымының қайтымды ПЖЕ-сі
 (1.40)
(1.40)Қайрылған жылылықтың әсері
 (1.41)
(1.41)Бақылау сұрақтары
-
Отынды үнемдеу мен қоршаған ортаны сақтаудың маңыздылығы. -
Жылуқозғалымдық айналымдардың ең тиімді түрлері. -
ЖЭО-ның өнімділік көрсеткіштері. -
Жылу электр станцияларының негізгі қағидалы сүлбелері. -
Су мен су буының жылу физикалық қасиеттерінің hs – сызбағы. -
Ренкин айналымының пайдалы жұмыс еселеуіштері мен жылулық және шықтық электр станциялардың отын шығындарын анықтау есебі. -
ЖЭО-ның сағаттық отын шығынын анықтау есебі. -
ЖЭО айналымының отын өнімділігін анықтау есебі. -
Қайрылған жылулықтың әсерін анықтау есебі.
2 Жылуөткізгіштік пен жылуөту
m=1 n=5
2.1 Тапсырма. Денелердің жылуөткізгіштік еселеуішін тікмегзем
әдісімен анықтау
Жылуөткізгіштігі анықталатын дене өресі r =10 мм мен қалыңдығы δ = 1 мм-лі сырықты табақшадан жасалған. Ол ыстықтықтары t1 = 120 + m + 0,2n=122 0C мен t2 = 20 + m + 0,2n=22 0C тұрақты, қалыптасқан жылулық ағыны Q = 23,2 Вт, екі үйектің арасында тығыз орналасқан. Зерттелетін дене өрелі жылулық ысыраптары болмастай өтеуленген (2.1 суретті қараңыз).
Зерттелген дененің жылуөткізгіштік λ еселеуішін анықтаңыз.
2.1 Тапсырма шешімі (m =1 n = 5).
Зерттелген дененің жылуөткізгіштік λ еселеуішін қалыптасқан жылы-лықтың кейіптемесімен табамыз


(2.1)
 (2.2)
(2.2)m =1 n = 5 түрлемінің жауабы λ ═ 0,739 Вт/(м∙К).
Бақылау сұрақтары
1. Жылуөткізгіштік еселеуіштің анықтаушы ыстықтығы не болады?
2. Жылуөткізгіштік еселеуішті ыстықтыққа тәуелді қалай анықталады?
3. Нақты жағдайлардағы есептің әдісі қандай болады?
4. Неліктен зерттелетін дененің мөлшерлері δ << r болуға тиіс?
5. Денелердің жылуфизикалық қасиеттерін зерттеу неліктен маңызды?
2.2 Тапсырма. Жылуөту
m=1 n=5
Пештің шамот кірпішінен жасалған қабырғасының жылуөткізгіштік еселеуіші
Жылуөту еселеуіші k, Вт/(м2·К) мен жылу ағынының тығыздығы q, Вт/м2 және қабырғаның tб1 мен tб2 бет ыстықтықтарын дәлдігі 5 пайыз жуықты әдіспен анықтаңыз.
2.2 Тапсырма шешімі (m =1 n = 5).
Төрт белгісіздерді анықтау үшін келесі кейіптемелерді аламыз

 (2.4)
(2.4)Пештің қабырғасының жылуөткізгіштік еселеуішінің ыстықтыққа сызықты тәуелділігі арқылы оның (2.4)-тегі аумаққылық орта мәні белгілі шекті мәндерінің арифметикалық орта мәніне тең екенін көреміз
 (2.7)
(2.7)Белгісіз tб1 мен tб2-лермен анықталатын (2.7)-дегі λ1 мен λ2-лер де белгісіз болады. Сондықтан λор – бесінші белгісіз шама. Жылуөту еселеуіші
 (2.8)
(2.8)(1.3) ÷ (1.5)-терден шығатынынан, мұнда бесінші тәуелсіз теңдеу болмайды.
Сонымен, (1.3) ÷ (1.6) теңдеулердің жүйесі тұйықталмайтындықтан, есепті біртіндеп жуықтау әдісімен (БЖӘ) шешеміз.
БЖӘ-нің бірінші жуықтысы ретінде қабырғаның орта ыстықтығы деп оны қоршаған жылутасығыштар ыстықтықтарының арифметикалық орта мәнін аламыз tбор' ≈ (1200 + 30)/2 = 650 0С. Анықталатын жылуөткізгіштік пен жылуөту еселеуіштері және жылу ағынының тығыздығы мен қабырғаның бет ыстықтықтарының бұған сәйкесті бірінші жуықты мәндерін табамыз
λор'═0,84(1+0,695∙10-3∙612)═1,219 Вт/(м∙К), (2.7')

 (2.8')
(2.8')q' = k'(tс1 – tс2) = 2,974(1194 - 30) =3461,736 Вт/м2, (2.6')
tc1' = tс1 – q'/α1 =1194 – 3461,736/32 = 1085,82 0С, (2.3')
tc2' = tс2 + q'/α2 = 32 + 3461,736/10 = 376,173 0С. (2.5')
БЖӘ-нің екінші жуықтысы ретінде қабырғаның орта ыстықтығы деп оның бірінші жуықтысындағы бет ыстықтықтарының арифметикалық орта мәнін алып, бұған сәйкесті жылуөткізгіштік пен жылуөту еселеуіштері және жылу ағыны тығыздығының (екінші жуықты) мәндерін табамыз
tбор" ≈ (tб1' + tб2')/2 ═ (1085,82 + 376,173)/2 ═ 725 0С, (2.9")
λор"═0,84(1+0,695∙10-3∙730,996)═1,2667 Вт/(м∙К), (2.7")

 (2.8")
(2.8")q" = k"(tс1 – tс2) = 3,044(1194 - 30) =3543,216 Вт/м2. (2.6")
Жылу ағыны тығыздығының бұл мәніндегі қабырғаның бет ыстықтықтары мен қабырғаның орта ыстықтығы және бұған сәйкесті жылуөткізгіштік еселеуішінің үшінші жуықтаудағы орта мәні келесіге тең
tб1" = tс1 – q"/α1 =1194 – 3543,216/32 = 1083,2745 0С, (2.3")
tб2" = tс2 + 21/α2 = 30 + 3543,216/10 = 384,3216 0С, (2.5")
tбор"' ≈ (tб1" + tб2")/2 ═ (1083,2745 + 384,3216)/2 ═ 733,798
0С, (2.9"')
λор"'═0,84(1+0,695∙10-3∙733,798)═1,268 Вт/(м∙К). (2.7"')
Үшінші жуықтыда жылуөткізгіштік еселеуішінің орта мәні онша өзгерген жоқ, яғни, оның есептік дәлділігі берілгенінен келесідей көп жоғары
 (2.9)
(2.9)Сонымен, есеп аяқталады. Оның m =1 n = 2 түрлемінің жауабы ретінде бұл жолы екінші жуықты қорытындылары алынады
tб1 ≈ tб1" = 1083,2745 0С, tб2 ≈ tб2" = 383 0С, k ≈ k" ═ 3,044 Вт/(м2·К), q≈q"=3543,216 Вт/м2.
Кейде талдаулық күрделі шешімдердің орнына мүмкін дәлдікпен БЖӘ-ні пайдаланған ұтымды.
Бақылау сұрақтары
1. Пештің жылылық ысыраптарын қалай бағалап, азайтуға болады?
2. Пештің ішкі бетінің күйеленуі жылулық неге соғады?
3. Қабырғаның бет ыстықтықтары қалай тұрақталады?
4. α1, α2, k-лердің мәндерін өзара салыстырыңыздар.
5. 2.2 суреттегі ыстықтықтар α1, λ/δ, α2, k-лерге қалай байланысты?
6. БЖӘ-нің қаралған есептегі пайдалануын түсіндіріңіздер.
 2.3 Тапсырма. Сұйықтың жылуөткізгіштік
2.3 Тапсырма. Сұйықтың жылуөткізгіштікеселеуішін қыздырылған сым әдісімен анықтау
m=1 n=5
Сұйықтардың жылуөткізгіштік еселеуішін «қыз-дырылған сым» әдісімен анықтайтын аспапта (2.3 суретті қараңыз) платина сымы 3 пен кварц 2 түтікшенің аралығына май 1 құйылған. Платина сымының қосөресі мен ұзындығы d1 = 0,12 мм мен l = 90 мм; кварц түтікшенің ішкі және сыртқы қосөрелері d2 = 1 мм мен d3 = 3 мм және жылуөткізгіштік еселеуіші λ2 ═ 1,4 Вт/(м·К).
Жылулық ағыны Q = 1,8 + 0,1m + 0,02n=2 Вт пен платина сымының ыстықтығы tб1 = 106,9 + m + 0,2n=108,9 0C және кварц түтікшенің сыртқы бет ыстықтығы t