Файл: Надежность элементов, определенная по статистическим данным об отказах устройств.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 29

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Лабораторная работа 1

НАДЕЖНОСТЬ ЭЛЕМЕНТОВ, ОПРЕДЕЛЕННАЯ ПО СТАТИСТИЧЕСКИМ ДАННЫМ ОБ ОТКАЗАХ УСТРОЙСТВ

Ц е л ь р а б о т ы: изучить основные показатели надежности, дать оценку влиянию количества интервалов наблюдения и количества отказавших объектов за интервал наблюдения на основные показатели надежности.

Задание

Статистические данные об отказах устройств

Исходные данные:

Интервал времени: Δt = 4 103 ч;

Коэффициент изменения числа отказавших объектов: Kn = 0,9;

Число объектов наблюдения в начале испытаний: N0 = 106.

Таблица 1.1. Исходные данные

Интервал

наблюдения i
1
2
3
4
5
6
7
8
9
10

Число отказавших объектов на участке наработки,

Δni, %
1
3
7
13
15
20
12
13
9
7


Решение

Воспользуемся следующими формулами:

Рассчитаем границы интервалов наблюдения – начало интервала

tнi = (i – 1)Δt, ч; конец интервала tкi = i Δt, ч; среднюю наработку в интервале

, ч/

Рассчитаем число объектов N(tнi) и N(tкi), не отказавших в начале и

конце i-го интервала наблюдения.

Рассчитаем среднее число объектов, не отказавших на каждом интервале наблюдения: N( ) = .

Определим вероятность безотказной работы, плотность распределения и интенсивность отказа наработки до отказа по выражениям соответственно для каждого интервала наблюдения:


Р(t) =

q(t) =

λ(t) =

где – число объектов наблюдения в начале испытаний;

– число объектов, отказавших к моменту времени t;

– число отказавших объектов на участке наработки от t до t + t;

– интервал наработки;

– среднее число неотказавших объектов на участке наработки от t до t + Δt.

Результаты вычислений занесем в таблицу 1.2.

Таблица 1.2. Результаты вычислений

Интервал наблюдения
Показатели надежности

i
tнi, 103ч
tкi, 103ч
, 103ч
N(tнi)
N(tкi)
Р(tнi)
Р(tкi)
q( ), 10-3ч
N( )
λ( ), 10-3ч

1
0
4
2
106
105
1
0,990566
0,002358
105,5
0,00237

2
4
8
6
105
102
0,990566
0,962264
0,007075
103,5
0,007246

3
8
12
10
102
95
0,962264
0,896226
0,016509
98,5
0,017766

4
12
16
14
95
82
0,896226
0,773585
0,03066
88,5
0,036723

5
16
20
18
82
67
0,773585
0,632075
0,035377
74,5
0,050336

6
20
24
22
67
47
0,632075
0,443396
0,04717
57
0,087719

7
24
28
26
47
35
0,443396
0,330189
0,028302
41
0,073171

8
28
32
30
35
22
0,330189
0,207547
0,03066
28,5
0,114035

9
32
36
34
22
13
0,207547
0,122642
0,021226
17,5
0,128571

10
36
40
38
13
12
0,122642
0,113208
0,002358
12,5
0,02


Изменим число интервалов наблюдения, задав его равным 2Δt, объединив попарно число отказавших объектов на участке наработки Δni из табл. 1.2 первого и второго интервалов наблюдения, третьего и четвертого, … и т. д. Повторно выполнить задания, результаты расчетов занесем в таблицу 1.3.

Таблица 1.3. Результаты вычислений

Интервал наблюдения
Показатели надежности

i
tнi, 103ч
tкi, 103ч
, 103ч
N(tнi)
N(tкi)
Р(tнi)
Р(tкi)
q( ), 10-3ч
N( )
λ( ), 10-3ч

1
0
8
4
106
102
1
0,962264
0,004717
104
0,004808

2
8
16
12
102
82
0,962264
0,773585
0,023585
92
0,027174

3
16
24
20
82
47
0,773585
0,443396
0,041274
64,5
0,067829

4
24
32
28
47
22
0,443396
0,207547
0,029481
34,5
0,09058

5
32
40
36
22
12
0,207547
0,113208
0,011792
17
0,073529




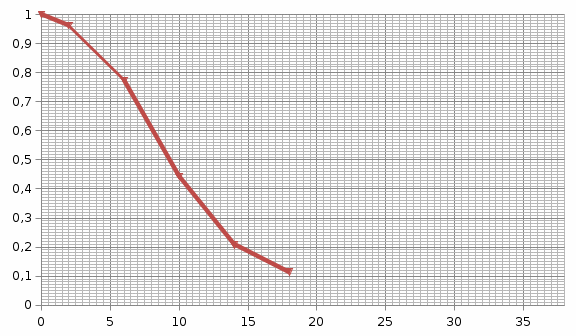
а



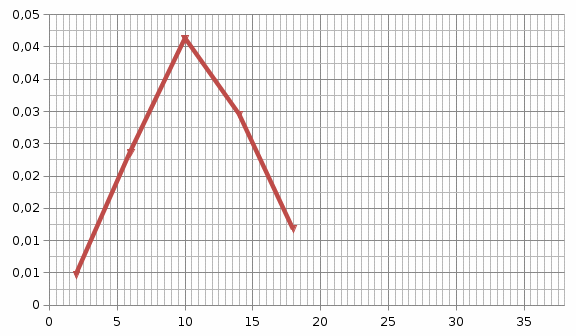
б



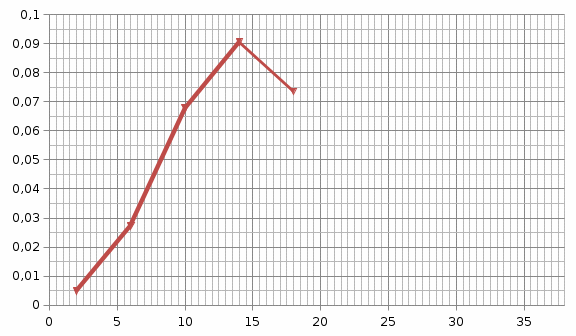
в

Рис. 1.1. Зависимости вероятности безотказной работы (а), плотности распределения наработки до отказа (б), интенсивности отказов (в) от количества интервалов наблюдения.

Уменьшим число отказавших элементов, задав его равным Kn ni и

повторно выполним расчеты, занесем их таблицу 1.4 и построим соответствующие графики (рис.1.2).

Таблица 1.4. Результаты вычислений

Интервал наблюдения
Показатели надежности

i
tнi, 103ч
tкi, 103ч
, 103ч
N(tнi)
N(tкi)
Р(tнi)
Р(tкi)
q( ), 10-3ч
N( )
λ( ), 10-3ч

1
0
4
2
106
105,1
1
0,991509
0,002123
105,55
0,002132

2
4
8
6
105,1
102,4
0,991509
0,966038
0,006368
103,75
0,006506

3
8
12
10
102,4
96,1
0,966038
0,906604
0,014858
99,25
0,015869

4
12
16
14
96,1
84,4
0,906604
0,796226
0,027594
90,25
0,03241

5
16
20
18
84,4
70,9
0,796226
0,668868
0,03184
77,65
0,043464

6
20
24
22
70,9
52,9
0,668868
0,499057
0,042453
61,9
0,072698

7
24
28
26
52,9
42,1
0,499057
0,39717
0,025472
47,5
0,056842

8
28
32
30
42,1
30,4
0,39717
0,286792
0,027594
36,25
0,08069

9
32
36
34
30,4
22,3
0,286792
0,210377
0,019104
26,35
0,07685

10
36
40
38
22,3
21,4
0,210377
0,201887
0,002123
21,85
0,010297



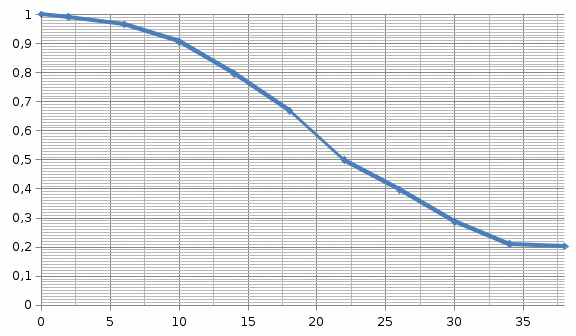
a



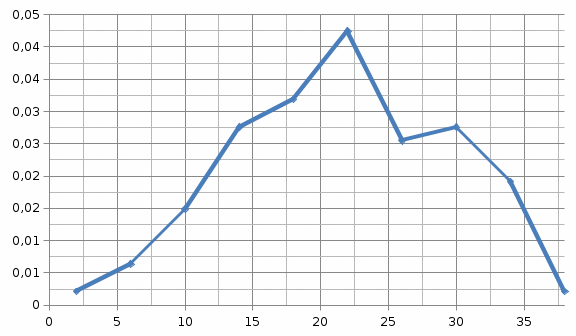
б



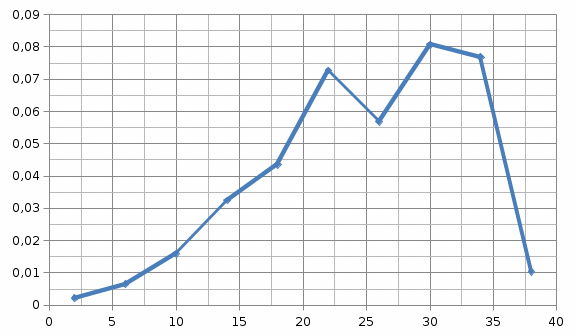
в

Рис. 1.2. Зависимости вероятности безотказной работы (а), плотности распределения наработки до отказа (б), интенсивности отказов (в) при уменьшении числа отказавших объектов.
Вывод: Как видно из расчетов и графиков (рис.1.1) при уменьшении интервалов как-бы сравниваются углы и лучше виден закон распределения к которому относятся данные отказы. При уменьшении числа отказавших объектов график безотказности работы выше предыдущего и уменьшение графиков плотности и интенсивности отказов в высоту (рис. 1.2.).


Лабораторная работа 2

НАДЕЖНОСТЬ ЭЛЕМЕНТОВ, ОПРЕДЕЛЕННАЯ

ПО ИЗВЕСТНЫМ ЗАКОНАМ

РАСПРЕДЕЛЕНИЯ НАРАБОТКИ ДО ОТКАЗА

Ц е л ь р а б о т ы: изучить основные законы распределения случайных величин, используемых в теории надежности, дать оценку влиянию основных параметров законов распределения на основные показатели надежности.

Исходные данные:

Параметры законов распределения случайных величин и коэффициент изменения параметров закона распределения:

α = 0,20 ч-1; m = 4,9 ч; σ = 0,2 ч; Кпар = 3,0

По экспоненциальному закону:

Рассчитаем наработку tпр:

tпр = = = 25 ч

Определим интервал наработки Δt:

Δt = = = 2,5 ч

де k - количество интервалов наблюдения, k =10.

Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i –

Смотрите также файлы