Файл: Надежность элементов, определенная по статистическим данным об отказах устройств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа по выражениям:
Р(t) =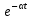 ;
;
q(t) = α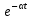 ;
;
λ(t) =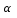
T0 = α-1
Результаты расчетов занесем в таблицу 2.1.
Изменим параметр экспоненциального закона распределения, задав его
равным Кпар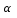 = 3,0
= 3,0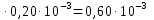 и повторить расчет.
и повторить расчет.
Рассчитаем наработку tпр:
tпр = =
= 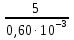 = 8,33
= 8,33 ч
ч
Определим интервал наработки Δt:
Δt = =
= 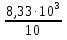 = 0,833
= 0,833 ч
ч
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты расчетов также занесем в таблицу 2.1.
Таблица 2.1 Результаты расчетов
Построим графики зависимости P(t), q(t), λ(t).
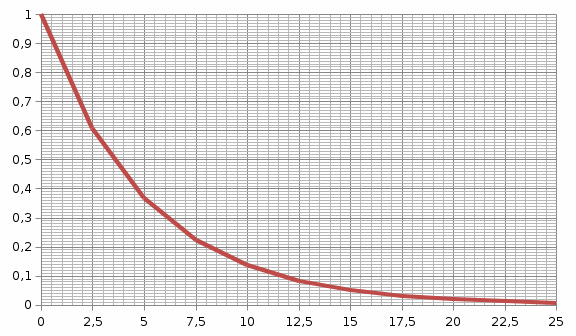
а
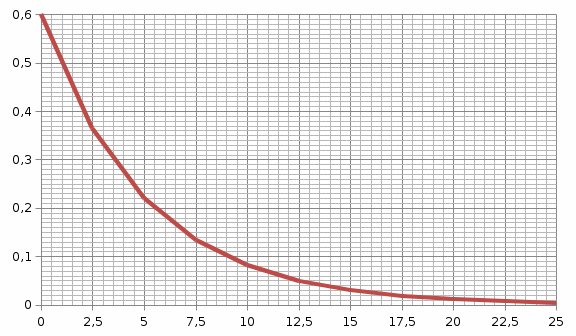
б
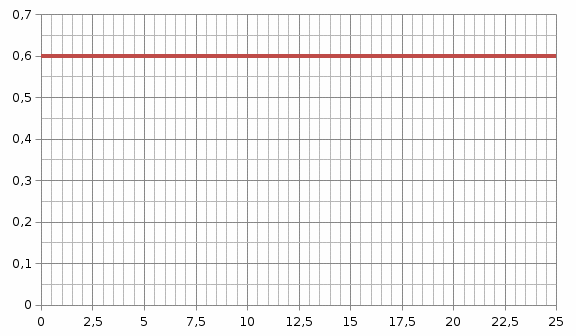
в
Рис. 2.1. Влияние параметров экспоненциального закона распределения на вероятность безотказной работы (а), плотность распределения наработки до отказа (б), интенсивность отказов (в).
Вывод: При экспоненциальном законе, на основании полученных зависимостей (рис. 2.1) при увеличении параметра α, уменьшается вероятность безотказной работы, увеличиваются плотность и интенсивность отказов, уменьшается средняя наработка до отказов.
По нормальному закону распределения:
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 4,9 - 3
- 3 0,2
0,2 = 4,3
= 4,3 ;
;
tпр = m + 3σ = 4,9 + 3
+ 3 0,2
0,2 = 5,5
= 5,5
Определим интервал наработки Δt:
Δt =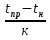 =
= 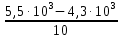 = 0,12
= 0,12 ч
ч
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа по выражениям:
Р(t) =1 -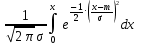 ;
;
q(t) =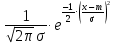 ;
;
λ(t) =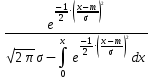
T0 = m
Результаты расчетов занесем в таблицу 2.2.
Изменим параметр нормального закона распределения, задав его
равным Кпар m и повторить расчет:
m и повторить расчет:
m = 4,9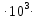 3,0 = 14,7
3,0 = 14,7
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 14,7 - 3
- 3 0,2
0,2 = 14,1
= 14,1 ;
;
tпр = m + 3σ = 14,7 + 3
+ 3 0,2
0,2 = 15,3
= 15,3
Определим интервал наработки Δt:
Δt = =
= 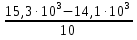 = 0,12
= 0,12 ч
ч
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты вычислений занесем в таблицу 2.2.
Изменим параметр нормального закона распределения, задав его
равным Кпар σ и повторить расчет: σ = 3
σ и повторить расчет: σ = 3 0,2
0,2 = 0,6
= 0,6
.
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 4,9 - 3
- 3 0,6
0,6 = 3,1
= 3,1 ;
;
tпр = m + 3σ = 4,9 + 3
+ 3 0,6
0,6 = 6,7
= 6,7
Определим интервал наработки Δt:
Δt = =
= 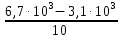 = 0,36
= 0,36 ч
ч
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты вычислений занесем в таблицу 2.2.
Таблица 2.2 Результаты расчетов
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа по выражениям:
Р(t) =
q(t) = α
λ(t) =
T0 = α-1
Результаты расчетов занесем в таблицу 2.1.
Изменим параметр экспоненциального закона распределения, задав его
равным Кпар
Рассчитаем наработку tпр:
tпр =
Определим интервал наработки Δt:
Δt =
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты расчетов также занесем в таблицу 2.1.
Таблица 2.1 Результаты расчетов
| Интервал наблюдений, i | Параметры закона распределения | |||||||||
| первоначальный | измененный | |||||||||
| ti, 103ч | P(t) | q(t), 10-3/ч | λ(t), 10-3/ч | Т0, 103ч | ti, 103ч | P(t) | q(t), 10-3/ч | λ(t), 10-3/ч | Т0, 103ч | |
| 0 | 0 | 1 | 0,2 | 0,2 | 5 | 0 | 1 | 0,6 | 0,6 | 1,67 |
| 1 | 2,5 | 0,60653 | 0,12131 | 0,83 | 0,6067 | 0,364 | ||||
| 2 | 5 | 0,36788 | 0,07358 | 1,67 | 0,3680 | 0,2208 | ||||
| 3 | 7,5 | 0,22313 | 0,04463 | 2,5 | 0,2233 | 0,1340 | ||||
| 4 | 10 | 0,13534 | 0,02707 | 3,33 | 0,1354 | 0,0813 | ||||
| 5 | 12,5 | 0,08209 | 0,01642 | 4,17 | 0,0822 | 0,0493 | ||||
| 6 | 15 | 0,04979 | 0,00996 | 5,0 | 0,0499 | 0,0299 | ||||
| 7 | 17,5 | 0,030197 | 0,006039 | 5,83 | 0,0302 | 0,0181 | ||||
| 8 | 20 | 0,01832 | 0,00367 | 6,66 | 0,0184 | 0,0110 | ||||
| 9 | 22,5 | 0,01111 | 0,00222 | 7,5 | 0,0111 | 0,0067 | ||||
| 10 | 25 | 0,00674 | 0,00135 | 8,33 | 0,0067 | 0,0040 | ||||
Построим графики зависимости P(t), q(t), λ(t).

а

б

в
Рис. 2.1. Влияние параметров экспоненциального закона распределения на вероятность безотказной работы (а), плотность распределения наработки до отказа (б), интенсивность отказов (в).
Вывод: При экспоненциальном законе, на основании полученных зависимостей (рис. 2.1) при увеличении параметра α, уменьшается вероятность безотказной работы, увеличиваются плотность и интенсивность отказов, уменьшается средняя наработка до отказов.
По нормальному закону распределения:
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 4,9
tпр = m + 3σ = 4,9
Определим интервал наработки Δt:
Δt =
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа по выражениям:
Р(t) =1 -
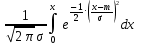 ;
;q(t) =
λ(t) =
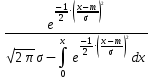
T0 = m
Результаты расчетов занесем в таблицу 2.2.
Изменим параметр нормального закона распределения, задав его
равным Кпар
m = 4,9
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 14,7
tпр = m + 3σ = 14,7
Определим интервал наработки Δt:
Δt =
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты вычислений занесем в таблицу 2.2.
Изменим параметр нормального закона распределения, задав его
равным Кпар
.
Рассчитаем начальную наработку tн и наработку tпр:
tн = m - 3σ = 4,9
tпр = m + 3σ = 4,9
Определим интервал наработки Δt:
Δt =
де k - количество интервалов наблюдения, k =10.
Рассчитаем наработку для всех интервалов наблюдения: ti = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.
Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.
Результаты вычислений занесем в таблицу 2.2.
Таблица 2.2 Результаты расчетов
| Интервал наблюдений, i | Параметры закона распределения | ||||
| Первоначальные параметры закона распределения | |||||
| ti, 103ч | P(t) | q(t), 10-3/ч | λ(t), 10-3/ч | Т0, 103ч | |
| 0 | 4,3 | 0,99865 | 0,022159242 | 0,022189195 | 4,9 |
| 1 | 4,42 | 0,991802 | 0,111972651 | 0,112898138 | |
| 2 | 4,54 | 0,96407 | 0,394750792 | 0,409462925 | |
| 3 | 4,66 | 0,88493 | 0,970930275 | 1,09718273 | |
| 4 | 4,78 | 0,725747 | 1,666123014 | 2,295735683 | |
| 5 | 4,9 | 0,5 | 1,994711402 | 3,989422804 | |
| 6 | 5,02 | 0,274253 | 1,666123014 | 6,075128801 | |
| 7 | 5,14 | 0,11507 | 0,970930275 | 8,437760124 | |
| 8 | 5,26 | 0,03593 | 0,394750792 | 10,98656514 | |
| 9 | 5,38 | 0,008198 | 0,111972651 | 13,65930598 | |
| 10 | 5,5 | 0,00135 | 0,022159242 | 16,41549327 | |
| Измененный параметр m | |||||
| 0 | 14,1 | 0,99865 | 0,022159 | 0,022189195 | 14,7 |
| 1 | 14,22 | 0,991802 | 0,111973 | 0,112898138 | |
| 2 | 14,34 | 0,96407 | 0,394751 | 0,409462925 | |
| 3 | 14,46 | 0,88493 | 0,97093 | 1,09718273 | |
| 4 | 14,58 | 0,725747 | 1,666123 | 2,295735683 | |
| 5 | 14,7 | 0,5 | 1,994711 | 3,989422804 | |
| 6 | 14,82 | 0,274253 | 1,666123 | 6,075128801 | |
| 7 | 14,94 | 0,11507 | 0,97093 | 8,437760124 | |
| 8 | 15,06 | 0,03593 | 0,394751 | 10,98656514 | |
| 9 | 15,18 | 0,008198 | 0,111973 | 13,65930598 | |
| 10 | 15,3 | 0,00135 | 0,022159 | 16,41549327 | |
| Измененный параметр σ | |||||
| 0 | 3,1 | 0,99865 | 0,007386414 | 0,007396398 | 4,9 |
| 1 | 3,46 | 0,991802 | 0,037324217 | 0,037632713 | |
| 2 | 3,82 | 0,96407 | 0,131583597 | 0,136487642 | |
| 3 | 4,18 | 0,88493 | 0,323643425 | 0,365727577 | |
| 4 | 4,54 | 0,725747 | 0,555374338 | 0,765245228 | |
| 5 | 4,9 | 0,5 | 0,664903801 | 1,329807601 | |
| 6 | 5,26 | 0,274253 | 0,555374338 | 2,025042934 | |
| 7 | 5,62 | 0,11507 | 0,323643425 | 2,812586708 | |
| 8 | 5,98 | 0,03593 | 0,131583597 | 3,662188381 | |
| 9 | 6,34 | 0,008198 | 0,037324217 | 4,553101993 | |
| 10 | 6,7 | 0,00135 | 0,007386414 | 5,471831092 | |