Файл: Урока Учитель математики Наумкина Светлана Анатольевна Тема урока Теорема Виета Класс 8 Дата 16. 03. 2023.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 45
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Технологическая карта урока
Учитель математики: Наумкина Светлана Анатольевна
Тема урока: Теорема Виета
Класс: 8
Дата: 16.03.2023.
Цель: формирование практико-ориентированной компетенции привыводе и доказательстве теоремы Виета и её применении при выполнении различных упражнений.
Задачи:
обучающие: экспериментальным путем выявить зависимость между корнями квадратного уравнения и его коэффициентами; доказать теорему Виета; сформировать умения применять её при решении типовых упражнений;
развивающие: развивать умения сравнивать, выявлять закономерности, обобщать, делать выводы;
воспитательные: воспитывать ответственное отношение к учебному труду.
Оборудование: компьютер, проектор, интерактивная доска, карточки с заданиями
Структура урока
-
Организационный момент (1 минута) -
Актуализация знаний. Создание проблемной ситуации. (6 мин.) -
Подготовка к изучению нового материала. (5 мин.) -
Изучение нового материала (10 мин.) -
Первичное осмысление и применение изученного (14 мин.) -
Подведение итогов урока (3 мин.) -
Постановка домашнего задания (1 мин.)
Ход урока
1.Организационный момент
Проверка готовности к уроку (рабочих тетрадей, учебников, письменных принадлежностей).
2.Актуализация знаний. Мотивация обучающихся.
«Неизвестное X, неизвестное Y,
Их можно в равенствах повстречать.
И это, ребята, скажу вам, не игры,
Здесь нужно решение всерьез отыскать.
С неизвестными равенства, без сомнения,
Называем, ребята, мы как?»
- О чем эта загадка? (Уравнения)
Подскажите, какую тему мы изучали? (Квадратные уравнения)
Проверяет Ромашка Блума (отрываем 7 лепестков в порядке цветов радуги):
Красный – Сформулируйте определение квадратного уравнения.
Оранжевый – Объясните, в чём заключается разница между приведенными и неприведенными квадратными уравнениями.
Жёлтый – Придумайте приведенное квадратное уравнение.
Зелёный – Составьте квадратное уравнение, в котором главный коэффициент равен 5, свободный член равен -25, второй коэффициент равен -20.
Голубой – Можем ли составленное нами уравнение 5
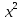-20x-25=0 сделать приведенным?
Синий – Поделитесь, какой способ решения частного случая квадратного уравнения вы знаете?
Фиолетовый – Можем ли решить уравнение х2 – 2012х + 2011 = 0. И как сократить затраты времени на решение этого уравнения? (решить можно, но долго вычислять)
Формулирование темы урока.
Разрешить этот вопрос поможет новая тема «Теорема Виета», а как звучит эта теорема сейчас мы узнаем.
(Предлагает заполнить таблицу в парах (слайд 5) и карточки с таким же заданием, организует ее проверку (слайд 6).)
3.Подготовка к изучению новой темы
| Уравнение | Х2-5х+6=0 | Х2-2х-15=0 | Х2+6х+8=0 |
| Корни уравнения | 2; 3 | -3 ;5 | -2;-4 |
| Коэффициент b | | | |
| Произведение корней | | | |
| Коэффициент c | | | |
| Сумма корней | | | |
(Предлагает найти закономерности по таблице и сделать выводы.)
С каким коэффициентом связано произведение корней? (c)
С каким коэффициентом связана сумма корней? (b) (слайд 7)
Формулируют гипотезу: сумма корней квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
4. Изучение нового материала
Эти соотношения впервые обнаружил французский математик Франсуа Виет. (Сведения из истории о Франсуа Виете (Cлайд 6))
Виет Франсуа (1540-1603) - французский математик, ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений. За это новшество его стали называть «отцом алгебры». Известны «формулы Виета», дающие зависимость между корнями и коэффициентами алгебраического уравнения.
(Предлагает рассмотреть доказательство Теоремы Виета)
На слайде: Сумма корней квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
По формулировке и доказательству теоремы Виета предлагает составить алгоритм решения приведенных квадратных уравнений. Записывают совместно алгоритм на доске.
| |
| |
| |
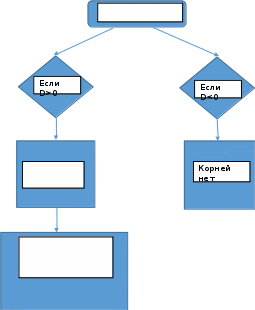
| Значит, как мы решим наше уравнение х2 – 2012х + 2011 = 0 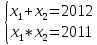 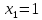 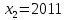 Показывает образец записи решения на доске А теперь решите уравнение х2+х+3=0. 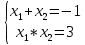 Почему невозможно подобрать корни? А от чего зависит количество корней? (Надо сначала найти Дискриминант) 5.Первичное закрепление знаний Решает совместно с учащимися квадратное уравнение. 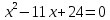 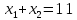 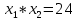 24=6*4=8*3=12*2=24*1/ 8+3=11 Ответ: 3; 8. z2+12z+20=0 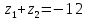 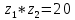 20=10*2=-10*(-2)=4*5=-4*(-5)=20*1=-20*(-1) -10+(-2)=-12 Ответ: -10; -2. 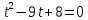 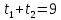 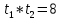 8=2*4=8*1 8+1=9 Ответ: 1; 8. 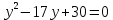 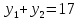 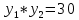 30=5*6=-5*(-6)=15*2=-15*(-2)=30*1=-30*(-1) 15+2=30 Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок, акцентирует внимание учащихся на значимости темы. 6.Подведение итогов урока Подводит итоги урока. Почему необходимо знать столько способов способ решения квадратных уравнений? Почему важно находить дискриминант при решении квадратных уравнений? 7.Постановка домашнего задания Выучить алгоритм решения квадратных уравнений. Решите уравнения из задачника №32.2-32.4 Составить «Синквейн» из предложенных словосочетаний, квадратное уравнение, полное, неприведенное, преобразовать уравнение, вычислить дискриминант, найти корни,знак дискриминанта – количество корней. Можно использовать свои словосочетания. |