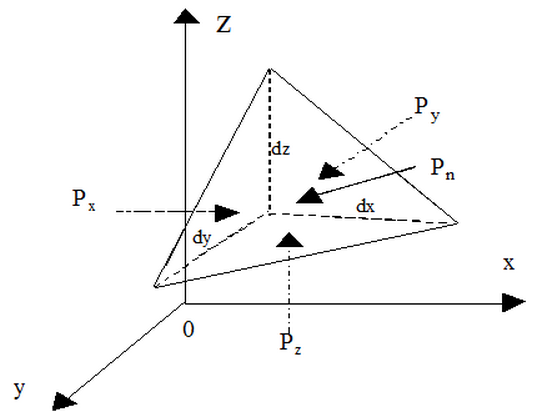
2.3-сурет. Гидростатикалық қысым қасиетін дәлелдеугеарналған сызба
Тік қабырғаға А - В; Р_хгоризанталды қабырғаға

В - С. Р және көлбеу қабырғаға А - С; Р_у.

Призмаға бұлардан басқа да салмақ күш әсері түседі,dG призманың салмағына тең: 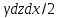. Сұйықтың тыныштық күйінде тепе-теңдік болуынан барлықкүштердің проекциядағы суммасы барлық бағыттағы

түсуі нөлге тең, яғни





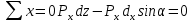
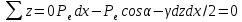
Табамыз:


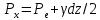
Егер призманың қырлары (қабырғалары) шексіз кеми берсе, ақырында ол нүктеге айналады, гидростатикалық қысым сол нүктеге түседі де әр түрлі бағытта болады, яғни Р_x = Р_z = Р_e(1.17). Сондықтан көлбеу жазыққа түсетін қысым Р_eшама жағынан тік қабырғаға түскен Р_x жөне горизанталды қабырғаға түскен Р_zкүшке тең болады да, көлбеу жазықтың ойша алына салған бұрышы ешқандай әсерін тигізбейді, бұл қасиетінің дәлелденуі бойынша сұйықтың қандай нүктесіне түскен күш барлық бағытқа бірдей тарайды.

Үшінші қасиеті. Нүктедегі гидростатикалың қысым оның кеңістіктегі координатасына байланысты болады, яғни:


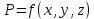
Нүктенің сұйық бетінен тереңдеген сайын гидростатикалық қысымы артады немесе керісінше тереңдігі кеміген сайын сұйықтың гидростатикалық қысымы кемиді. Сұйықтың бұл қасиеті арнайы дәлелдеуді қажет етпейді.
Сұйықтың тепе-теңдігінің дифференциалды тендеуі (Эйлер теңдеуі)

Тыныштық қалпындағы сұйықта қысымның таралу заңын анықтау үшін салыстырмалы тыныштықтағы сұйықтың жалпы тепе-теңдік жағдайын қарастырамыз. Ол тыныштықта тұрған сұйықтың ішіндегі шексіз өте кішкене шамадағы параллелепипедті алып, оның қабырғаларын dх, dу, dг деп белгілеп, (2.4-сурет) параллелепипедтің сыртқы қабырғасына түсетін сұйықтың өсерін гидростатикалық қысыммен алмастырамыз. Қаралап отырған параллелепипед мына сыртқы күштердің әсерімен тепе-теңдік жағдайда болады:

а) параллелепипедтің қабырғаларына перпендикуляр болып бағытталған айналадағы сұйықтың жазықтық күші деп аталатын қысым күші;

---

ә) сұйықтың әр бөлшегіне өсер ететін масса немесе

көлемдік күштер.

Онда параллелепипедтің сол жақ қабырғасына түсетін сұйықтың қысым күші А нүктесіне түсетін гидростатикалық күшті қабырға ауданының көбейтіндісіне тең болады:


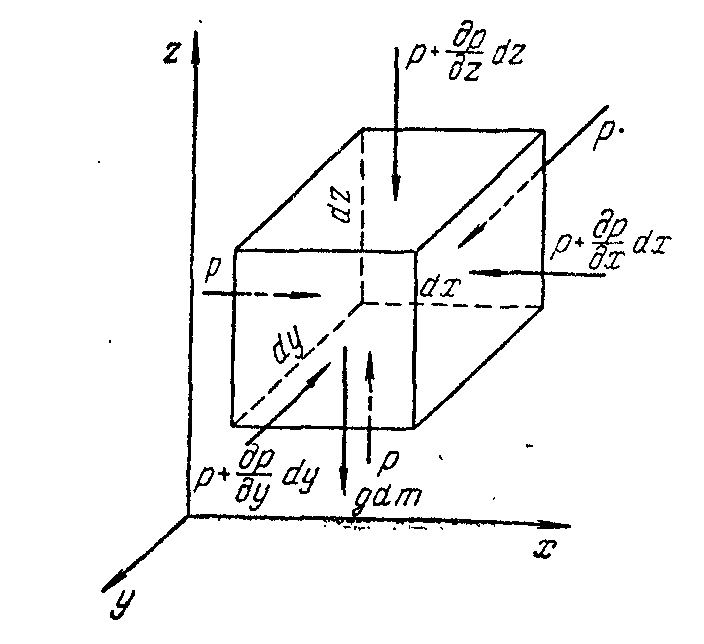
2.4-сурет. Сұйықтың тепе-теңдігінің дифференциалды

теңдеуін шығаруға арналған сызба


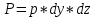
ал оң жақ қабырғаға түсетін қысым күші:



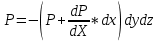
Сол жақ қабырғаға түсетін қысым күші ОХ осімен бағыттас болып, ол - оң шамада, ал оң жақтағы қабырғаға түскен күш, керісінше бағытталған, сондықтан оның таңбасы - теріс. ОХ осіндегі көлем күшінің проекциясы осындағы dх, dу, dz - параллелепипедтің массасы параллелепипедке түсетін барлық күштердің X осіндегі проекциясының жинаған және осы суммасын нөлге теңеп табамыз:


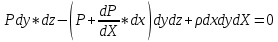
Бүдан:

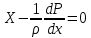
Осы теңдеу сияқты у және zшамаларын табады. Онда:
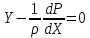және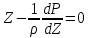
Сұйықтың тепе-теңдік дифференциалды теңдеуін 1755 жылы Л.Эйлер есептеп шығарған.
Гидростатиканың негізгі заңының геометриялық

және физикалық сипаттамасы

Гидростатиканың негізгі заңын толық қарастыралық.



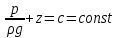
Ондағы 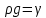алмастырылып және интегралдаудың тұрақтысын былай табамыз: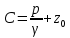



егер Р =P₀ және Z=Z₀, онда гидростатикалық негізгі теңдеуін А және В нүктелері үшін:

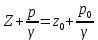немесе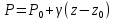
Сұйық бетінен төмен орналасқан А нүктесі үшін негізгі гидростатикалық теңдеуі былай жазылады. Р = Р₀+ һ, мұндағы, Р - толық немесе абсолютті қысым-Р_абс;

---

- салмақты қысым, бірлік аудандардағы һ - тереңдігі, Zжәне Z₀ — оймен алына салған салыстырмалы 0 — 0 жазықтықтан А және В нүктесіне дейінгі геометриялық биіктік,оны салыстыру жазықтығы деп атайды; Р/ және Р₀/ -биіктік, А және В нүктелеріндегі гидростатикалық қысым. Zжәне Р₀/ шамасын гидравликада геометриялық және пьезометрлік биіктік немесе геометриялық және пьезометрлік тегеурін деп атайды. Геометриялық және пьезометрлік екі биіктіктің қосындысын толық гидростатикалық биіктік деп атайды: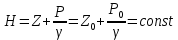

Бұл теңдеу бойынша тепе-теңдік қалпындағы біртекті сұйықтың барлық нүктелерінде геометриялық және пьезометрлік биіктіктердің қосындысы тұрақты шама болып саналады. Гидростатиканың негізгі теңдеуінің графигі есептеу жазықтығын Н биіктігімен параллель болып жүргізілген көлденең жазықтық (0-0) болып бейнеленеді.

Осы есептеу жазықтығынан Н биіктігінде жатқан көлденең жазықтықты тегеурін жазықтығы деп атайды. Егер сұйықтың еркін бетіндегі қысым атмосфера қысымына тең болса, тегеурін жазықтығы сұйықтың еркін бетімен бірдей болады.

Физикалық тұрғыдан қарағанда гидростатиканың негізгі теңдеулерінің мүшелерінің (Н = 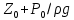) қосындысы мен g үдеуінің көбейтіндісіне тепе-теңдік қалпындағы сұйықтың меншікті потенциалды энергиясы деп есептейді. Меншікті потенциалды энергия деп потенциалды энергияның сұйық массасына қатынасын айтады. Мысалы, gz- сұйықтың жер жағдайындағы биіктігінің меншікті энергиясы; ал g• Р / = Р / = р / - сұйықтың қысымының меншікті энергиясы деп атайды.

Теңдеу (2.24) гидростатикалық қысым Р сұйықтың қай нүктесінде және қандай тереңдігінде болсын, еркін бетіне түскен сыртқы қысым Р₀ байланысты болады, яғни тыныштықта тұрған сұйықтың еркін бетіне сырттан түсетін қысым күшінің әсері, сұйықтың ішіндегі қай нүктесі болсын ешбір өзгеріссіз тартылып беріледі. Міне, бұл - тәжірибе түрінде табылған Паскаль заңының негізгі тұжырымдамасы.

---

Гидростатикалық қысымды өлшеу құралдары

Қысымның мынадай түрлері ажыратылады: барометрлік, абсолютті, манометрлік және ваккумметрлік.

Барометрлік қысым (кейде атмосфералық) Р₀ белгілейді, бұл теңсіз бетінің қандай биіктігіне және ауа райының жағдайымен тығыз байланысты болады.

Нормалы барометрлі қысым 760 мм сынап бағанасына тең, яғни 101325Н/м². Биіктігі өскен сайын қысым кеми береді:мысалы, теңіз деңгейінен 1000 м биіктікте нормалы қысымның 10 0/ 0-ге, 2000 м биіктікте 20 0/ 0-ге кемиді.

Абсолюттік қысым Р_абс гидростатиканың негізгі теңдеуі арқылы табылады:



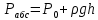
Егер сұйықтың ашық бетіне тіке ғана барометрлік қысым түссе, онда
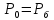және ,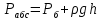
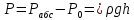
Бұл формуланы манометрлік немесе артық қысым дейді, егер Р_абс> Р_б, немесе Р_абс < Р_б, шама ваккуметрлік қысым деп аталады да, Р_вак = Р_б – Р_А . болады.

Манометрлік қысымды сұйық немесе серіппелі манометрмен өлшейді.

Ыдыстағы сұйықтың қысымын сұйықты манометрмен өлшейді, кейде мұндай аспапты пьезометр деп атайды (2.7-сурет).



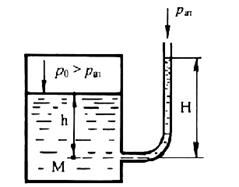
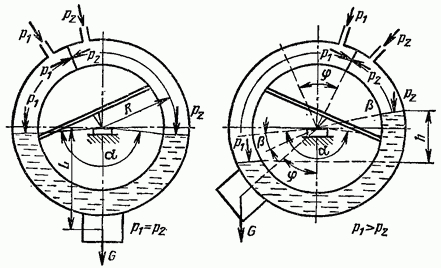
2.7-сурет. Сұйықты манометр

Сынапты манометр (2.8-сурет) қысымды өлшеу кезінде жиі қолданылады. Сұйық ішіндегі екі нүктенің қысым айырмашылығын табу үшін (мысалы екі ыдыстағы немесе бір құбыршаның) түтік (ішіндегі тек әр түрлі нүктедегі) арқылы, дифференциалды манометр қолданылады.

Серіппелі манометрлер мембраналы және түтікшелі болып бөлінеді. Мембраналық манометрдің негізгі бөлшегі ирек-ирек (V) мембрана. Қысым өлшеу кезінде, барометрлік қысымнан артық болса, V мембрана майысады да, көрсеткіш межелік (шкала) қозғалады. Түтік манометрдің жүмыс істеу тәртібі негізгі бөлшегі - түтік (К), қысым артқанда түтік жазылыңқырайды да нұсқар (стрелка) жылжиды (2 .8-сурет).



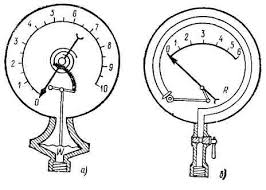
2.8-сурет. Пластинкалы манометр

Ваккуметрлік қысымды ваккуметрмен өлшейді. Өте көп тараған түрлері: сұйықты және серіппелі түрлері.Сұйықты ваккуметр - түтікшесінен тұрады, ол ваккуметрлік қысым өлшегіш ыдыспен жалғасқан (S), ал басқа бөлігі (түтікшенің) ыдыстағы тығыздығы белгілі сұйықпен жалғасқан.

---

Т - түтікшесіндегі, К - нүктесіндегі гидростатикалық негізгі теңдеуін жазамыз:


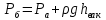
Бұдан:

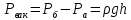немесе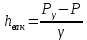

Сонымен сұйықтың тығыздығымен һ_вак білсек, онда Р_вак табуға болады. Серіппелі ваккуметрдің жұмыс істеуі серіппелі манометрмен бірдей.
Сұйықтың гидростатикалық қысым күшінің жазық және қисық бетке түсуін анықтау

Гидростатиканың негізгі теңдеуін пайдалана отырып, сұйықтың көлбеу жазықтық қабырғасына кейбір бұрышпен ( 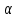) түскен гидростатикалық қысымның күшін толық табу. Қаралып отырған учаскедегі 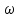көлеміне сұйық жақтан келіп түсетін қысым күшін есептеп шығарамыз. О_х сызық бойымен қабырға жазықтығымен жалғасып сұйықтың ашық бетімен кездеседі де, у осімен 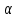бұрышында болады. Шексіз аз ғана элементарлы көлемге түскен қысым күші: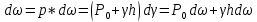



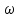Мұндағы, Р₀ - сұйықтың ашық бетіне түсетін қысым; - меншікті салмақ; - элементарлы ауданшаның һ тереңдіктегі орналасуы. Гидростатикалық толық қысым күшін анықтау үшін формуласымен барлық 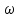ауданы бойынша интегралдап табамыз: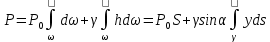



мұндағы, у - ауданша көлемінің центр координатасы, һ = уsin 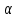интеграл

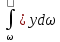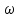, - жазықтың ауданының ОХ осіндегі статикалық моменті бойынша сол ауданның ауырлық ортасы координатасының көбейтіндісіне тең болады (с нүктесі) .

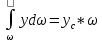Онда:

---

Смотрите также файлы

• Виды излучений. Шкала эмв с помощью какого вида излучений проводится флюорографическое обследование.docx

• 1. Зона то и Р Закрытая оттапливаемая мойка на 2 поста Ремонтный цех Техническая стоянка для тс, ожидающих ремонта (посты приёмки и выдачи) Открытый склад Парковочная зона для сотрудников 7.docx

• Задание 1 Переведите число 101010,012.docx

• 1. Дайте характеристику стретчинггимнастики.docx

• Операционнная система windows.docx