Министерство образования и науки Российской Федерации



Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский горный университет

Кафедра высшей математики

Расчетно-графическая работа

По дисциплине ______________Математика________________________

(наименование учебной дисциплине согласно учебному плану)

Тема работы: __ Основы математической статистики___

Вариант 106

Выполнил: ст. группы КРС-21 Крюков Т.В.

(должность) (подпись) (Ф.И.О)

Дата: ______________________________

Проверил: доцент Мансурова С.Е.

(должность) (подпись) (Ф.И.О)

Задача 1.

Статистическая обработка массива данных.

Выборочные оценки генеральной совокупности.

Условие задачи:

1) Составить сгруппированный статистический ряд:

а) определить нужное кол-во интервалов по формуле Стерджесса

k 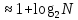, где N-объем выборки;

б) найти наибольшее и наименьшее значение измеряемой величины;

в) определить ширину интервала. Используемая формула:



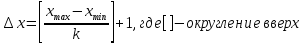
г) интервалы берутся открытыми слева и закрытыми справа: (α_i;β_i], i=1..k

д) концы интервалов вычисляются по формулам:



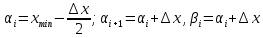
е) определить середины интервалов:

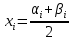
2) Для сгруппированного статистического ряда вычислить выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию, исправленное среднее квадратическое отклонение.

3) Считая генеральную совокупность нормально распределенной, найти интервальные оценки математического ожидания и среднего квадратического отклонения с надежностью 0,95

---

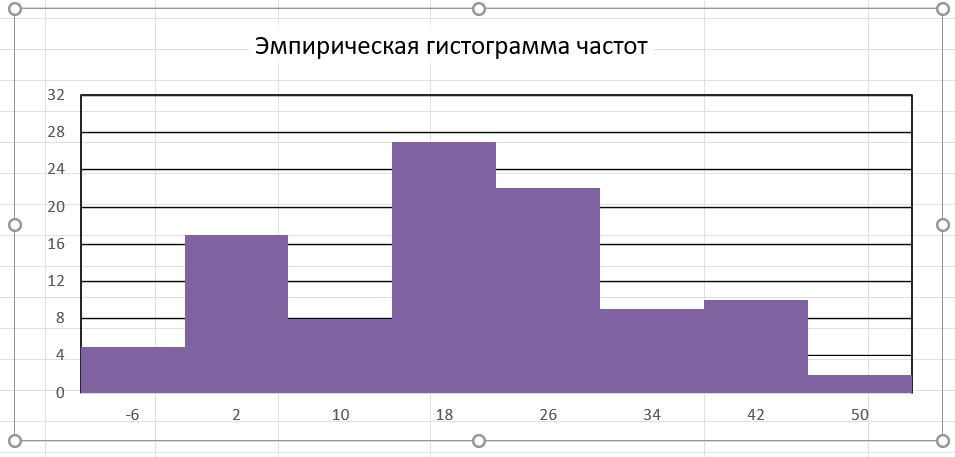
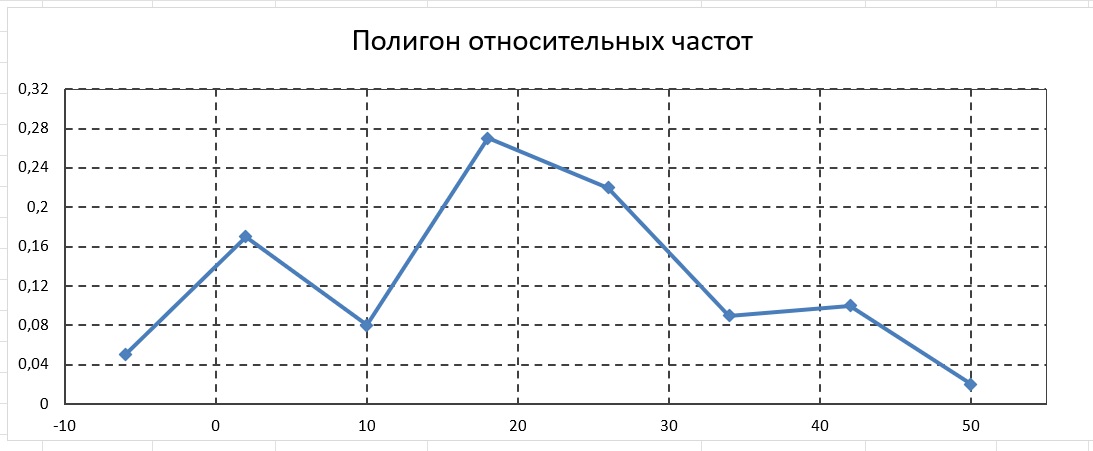
4) Построить гистограмму, полигон частот и эмпирическую функцию распределения.

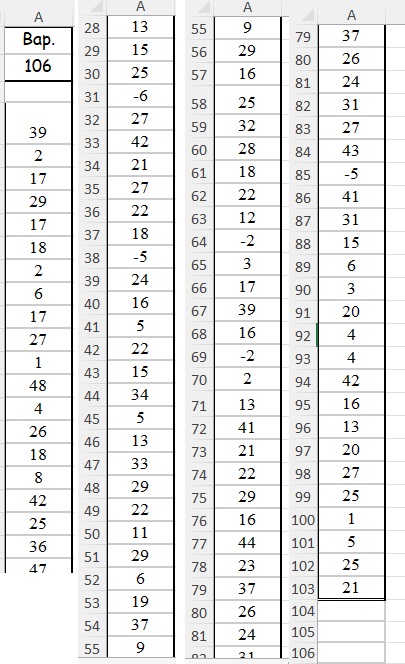
Исходные данные:



Решение:

1. 
   Объем выборки N=100. Определим кол-во интервалов для группировки по формуле Стеджесса:
   

k 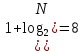, где […] – символ округления (вверх) до целого.

Найдем наибольшее и наименьшее значения измеряемой величины



Определим ширину интервала.



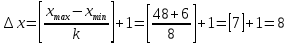
Составим таблицу со сгруппированным статистическим рядом:



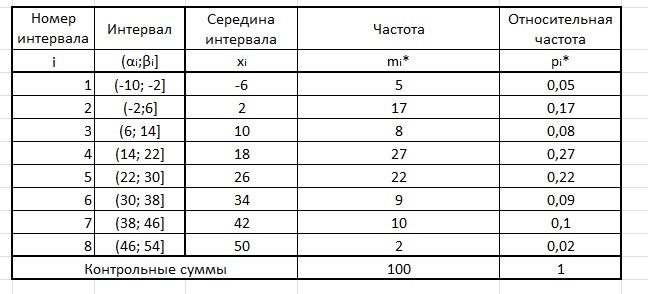
Рис.1. Таблица со сгруппированным статистическим рядом

Начало первого интервала вычисляется по формуле: 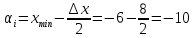; для остальных :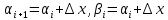

2)Числовые характеристики

(точечные оценки параметров генеральной совокупности)

Выборочное среднее:



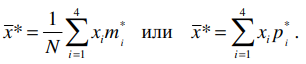
Выборочная дисперсия:



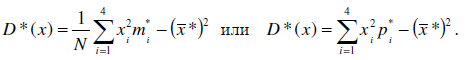
Выборочное среднее квадратическое отклонение:



Несмещенная дисперсия:



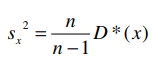
Исправленное среднее квадратическое отклонение

:

Полученные результаты из Excel:

3) Интервальные оценки параметров генеральной совокупности

Теория:1. Оценка мат. ожидания при неизвестной дисперсии

---

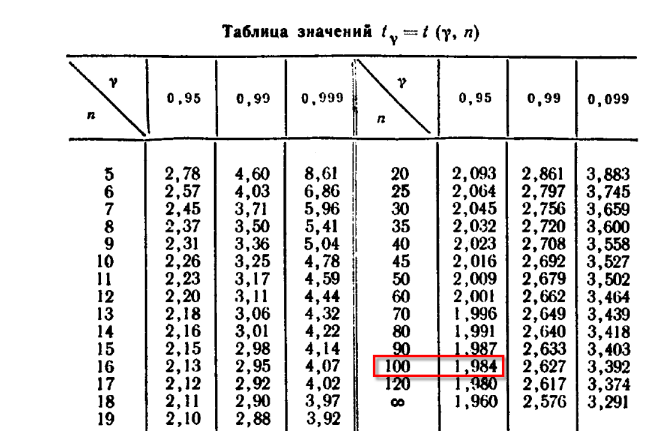
Для решаемой задачи: объем выборки N=100; надежность γ=0,95; исправленное квадратическое отклонение s=13,85. По таблице значений для t_γ находим: t_γ=1,984 (таблица значений ниже)

Тогда точность оценки (радиус доверительного интервала):



= =

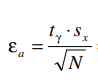
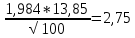
Таким образом, с вероятностью 0,95 математическое ожидание генеральной совокупности принадлежит интервалу (19,68-2,75; 19,68+2,75), т.е. 16,866


Теория: 2. Оценка ср.кв. отклонения.



По таблице значений для q(γ,N) находим: q(0,95;100) =0,143. Тогда концы доверительного интервала:





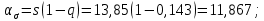
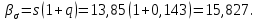
Таким образом, с вероятностью 0,95 среднее квадратическое отклонение генеральной совокупности принадлежит интервалу



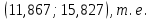
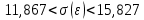
Результаты из Excel:



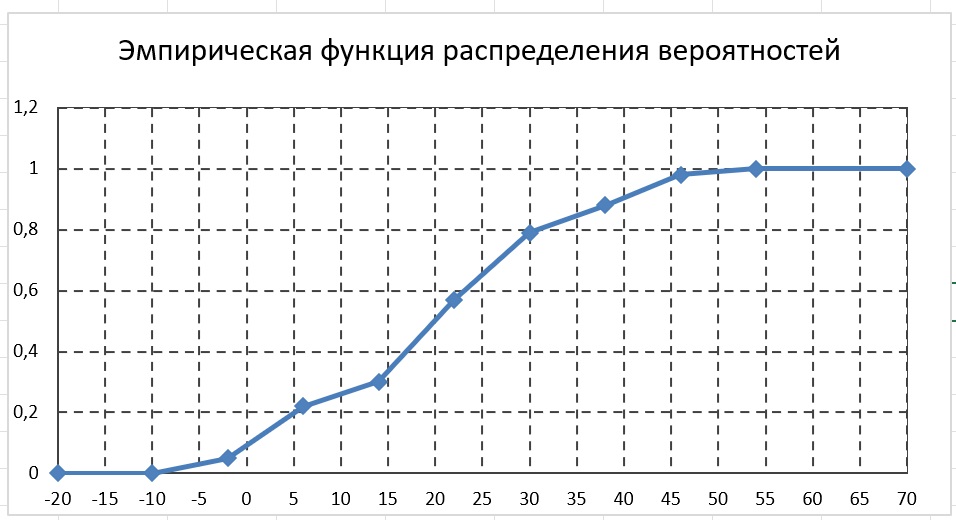
4)Гистограмма, полигон частот и эмпирическая функция распределения.





Для построения эмпирической функции распределения, с учетом группировки, лучше использовать не кусочно-постоянную, а непрерывную кусочно-линейную функцию, где до начала первого интервала и на левом конце первого интервала F* 0 , на правом конце первого интервала 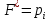на отрезке 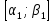строим функцию как отрезок, соединяющий конечные точки. На втором отрезке будет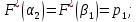

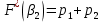и т.д. Таким образом, для последнего интервала получим:

---

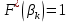и это же значение 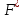будет иметь для всех значений х, больших, чем 54. При подобном рассмотрении эмпирической функции распределения вероятностей мы предполагаем, что изменения ее значений происходят не скачком в средних точках интервалов, а накапливаются "плавно" на каждом интервале.

Составим таблицу для построения описанной функции распределения:





Задача 2. Проверка статистических гипотез.

Условие задачи:

По данным из задачи 1:

1) Оценить с помощью критерия Пирсона хи-квадрат согласие данных с нормальным распределением при уровне значимости α=0,05

2) Построить сравнительный график эмпирических (ломаная линия с маркерами) и теоретических (сглаженная линия без маркеров) частот. График рисуется на белом фоне линиями разных цветов, добавляются линии сетки координат и легенда.

Решение:

Оценим с помощью критерия Пирсона хи-квадрат согласие эмпирических данных с нормальным распределением при уровне значимости α=0,05 .

Основная гипотеза Н₀: рассматриваемая генеральная совокупность ξ распределена по нормальному закону с параметрами 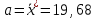и δ=δ*=13,78 ; альтернативная гипотеза Н₁: генеральная совокупность распределена по какому-то другому закону.

Для этого дополним таблицу со сгруппированным статистическим рядом значениями теоретических вероятностей теоретических частот.

Теоретические вероятности попадания значения генеральной совокупности в интервал вычисляются как 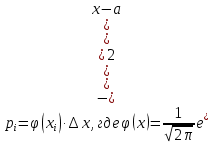плотность нормального распределения, i=1..k . Теоретические частоты вычисляются по формуле 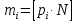, где [...] — округление до целого.

При этом контрольные суммы для теоретических вероятностей и частот должны приближенно равняться 1 и объему выборки.

Вычислив необходимые величины, получим:

---

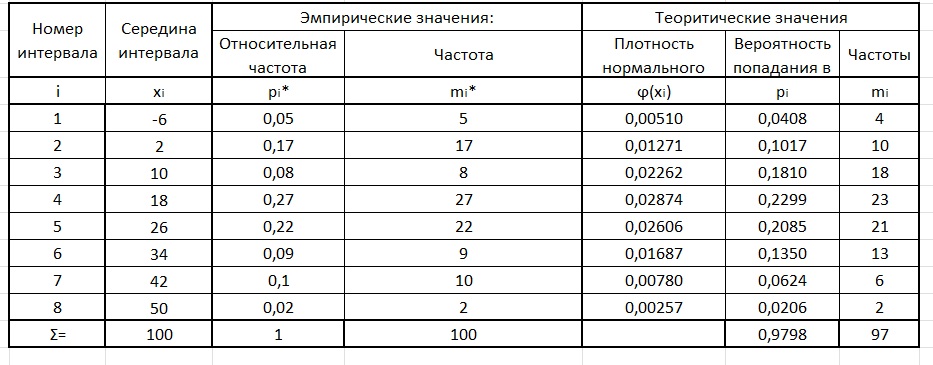
Т.к. критерий Пирсона не "работает" при малых частотах, объединим 1-й интервал со 2-ми 7й с 8-м. Таким образом, количество интервалов уменьшится до k =6.

Добавим в таблицу столбец с наблюдаемыми значениями распределения , где

Получим: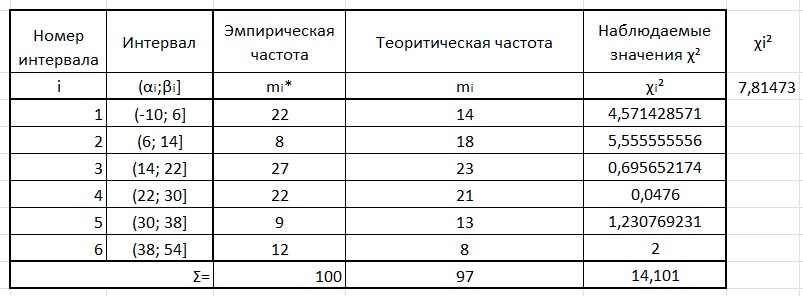



Таким образом, 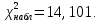По таблице критических точек распределения 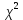найдем при числе степеней свободы n k 3 63 3 и уровне значимости 0,05 :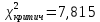



Сравнивая найденное значение 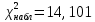с критическим (14,101> 7,815), определяем, что 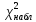лежит в критической области

Таким образом, при уровне значимости α=0,05 можно утверждать, что распределение рассматриваемой генеральной совокупности ξ сильно отличается от нормальной

Построим сравнительный график эмпирических (ломаная линия с маркерами) и теоретических (сглаженная линия без маркеров) частот (используя точечную диаграмму).



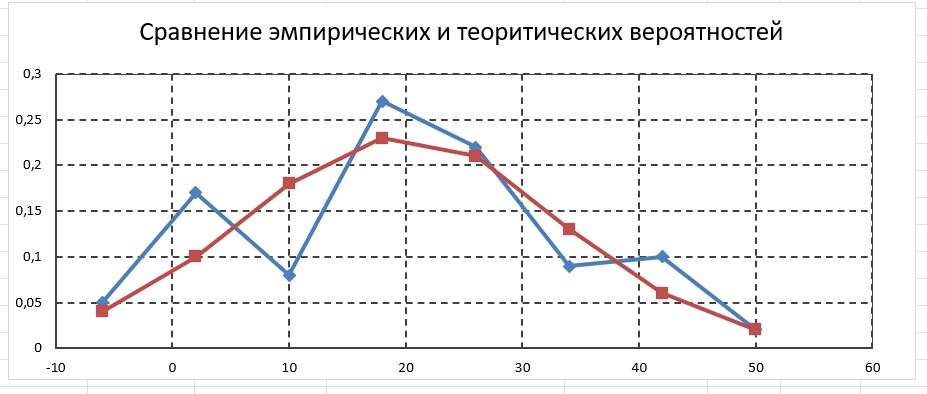
Задача 3. Корреляционный и регрессионный анализ данных.

Условие задачи:

1)Установить наличие или отсутствие связи между случайными величинами Х и У, вычислив выборочный коэффициент корреляции.

2)Найти выборочные регрессии У на Х и Х на У, предполагая, что они линейные

3)Построить линии регрессий и точки условных средних на одном чертеже (точки условных средних Х и регрессия Х и У изображаются одним цветом, а точки условных средних У и регрессия У на Х – другим цветом).

---

Смотрите также файлы

• алтайский государственный университет.docx

• 2. 1 Изучение фундаментальных основ современных технологий на уроках информатики и во внеурочной деятельности.docx

• Білім беру йымыны атауы Егіндікл жоббм пні.docx

• Допускаю к защите Руководитель Бочкарев В. А. Природоохранные технологии на тэс в городе Челябинск пояснительная записка к курсовой работе по дисциплине Природоохранные технологии на тэс 031. 00. 00. Пз.docx

• Обезбол билеты 1 билет.docx