Файл: Геометрия пнінен Жиынты баалауа арналандістемелік сыныстар 10сынып.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 136
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«Геометрия» пәнінен
Жиынтық бағалауға арналғанәдістемелік ұсыныстар
10-сынып
(қоғамдық-гуманитарлық бағыты)
Нұр-Сұлтан – 2019
Әдістемелік ұсыныстар мұғалімге 10-сынып білім алушыларына «Геометрия» пәні бойынша жиынтық бағалауды жоспарлау, ұйымдастыру және өткізуге көмек құралы ретінде құрастырылған. Бөлім бойынша жиынтық бағалаудың тапсырмалары мұғалімге білім алушылардың тоқсан бойынша жоспарланған оқу мақсаттарына жету деңгейін анықтауға мүмкіндік береді.
Әдістемелік ұсыныста бөлім бойынша жиынтық бағалауды өткізуге арналған бағалау критерийі мен дескрипторлары бар тапсырмалар ұсынылған. Сондай-ақ жинақта білім алушылардың оқу жетістіктерінің мүмкін деңгейлері (рубрикалар) сипатталған. Дескрипторлары мен балдары бар тапсырмалар ұсыныс түрінде берілген.
Әдістемелік ұсыныс мұғалімдерге, мектеп әкімшілігіне, білім беру бөлімінің әдіскерлеріне, критериалды бағалау бойынша мектеп, өңірлік үйлестірушілеріне және басқа да мүдделі тұлғаларға арналған.
Әдістемелік ұсынысты дайындау барысында ресми интернет-сайттағы қолжетімді ресурстар (суреттер, фотосуреттер, мәтіндер, аудио және бейнематериалдар) қолданылды.
2
МАЗМҰНЫ
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 4
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау 4
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 8
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 8
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 12
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 12
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 18
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» тарауы бойынша
жиынтық бағалау 18
3
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау
Тақырып Стереометрия аксиомалары және олардың салдарлары
Кеңістіктегі екі түзудің өзара орналасуы
Түзу мен жазықтықтың өзара орналасуы
Екі жазықтықтың өзара орналасуы
Оқу мақсаты
10.2.1 Стереометрия аксиомаларын, олардың салдарларын
білу және оларды математикалық символдар арқылы
жазып көрсету
10.2.2 Кеңістіктегі параллель және айқас түзулердің
анықтамаларын білу және оларды анықтау және
кескіндеу
10.2.3 Кеңістіктегі параллель түзулердің қасиеттерін білу
және оларды есептер шығаруда қолдану
10.2.4 Түзу мен жазықтықтың параллельдік және
перпендикулярлық белгілерін, қасиеттерін білу және
оларды есептер шығаруда қолдану
10.2.5 Жазықтықтардың параллельдігі мен
перпендикулярлығының белгілерін білу және
оларды есептер шығаруда қолдану
Бағалау критерийі Білім алушы
Стеореметрия аксиомаларын және олардың салдарын
қолданады
Кеңістіктегі түзулердің өзара орналасуын анықтайды
Түзу мен жазықтықтың параллельдік белгісін
қолданады
Жазықтықтардың параллельдік қасиетін қолданады
Ойлау дағдыларының Қолдану
деңгейі
Орындау уақыты 25 минут
Тапсырма
-
Берілген символдық жазу бойынша сызбаны салып, дәлелдеңіз:
( ∩ )= , ∈ , ∉ ⇨ ⊄
-
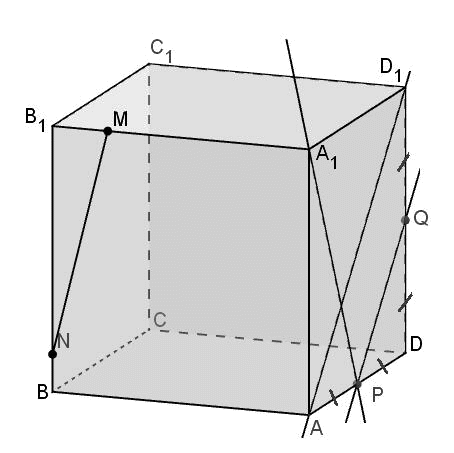
Төменде АВСDA1B1C1D1 текшесінің суреті берілген. Келесі түзулер жұбының орналасуын анықтаңыз:-
QP және AD1, мұндағы Q және Р сәйкесінше DD1 және AD кесінділерінің орталары;
-
-
AD1және A1P;
-
MN және AD1,мұндағыMжәне N сәйкесінше A1B1және BB1кесінділерінетиісті;
-
CD және A1 P;
-
MN және AB?
Қиылысатын түзулер үшін қиылысу нүктесін анықтаңыз, ал айқас және параллель түзулер үшін сәйкес белгіні қолданып жазыңыз.
4
-
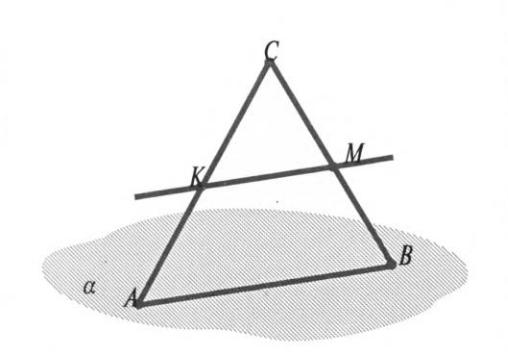
АВ кесіндісі15 см-ге тең жәнеαжазықтығында жатыр. С нүктесіαжазықтығынатиісті емес. К және М нүктелері сәйкесінше АС мен ВС кесінділерінің орталары.
а) КМ түзуінің α жазықтығымен ортақ нүктелері болуы мүмкін бе? Жауабыңызды негіздеңіз.
-
К және М нүктелерінің арақашықтығы неге тең?
-
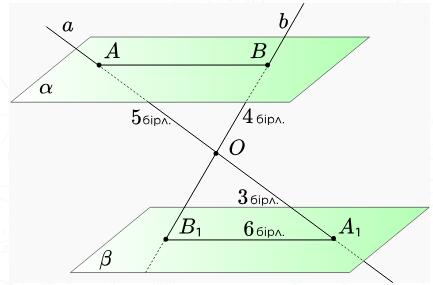
a және b түзулері О нүктесінде қиылысады.Олар және параллель жазықтықтарынсуретте көрсетілгендей, А, А1, В, В1 нүктелерінде қияды. АВ және ОВ1 ұзындықтарын табыңыз.
5
| Бағалау критерийі | Тапсырма | | | Дескриптор | | Балл | ||
| № | Білім алушы | | ||||||
| | | | | | ||||
| Стеореметрия | | | қиылысушы жазықтықтарды салады; | 1 | ||||
| аксиомаларын | және | 1 | сызбада PQ-дің β-ны қиғаны көрінеді; | 1 | ||||
| олардың | | салдарын | | | | | ||
| | | | | | | |||
| | аксиомаларды/салдарларды | қолданып | | |||||
| қолданады | | | | 1 | ||||
| | | | тұжырым жасайды; | | ||||
| | | | | | | |||
| Кеңістіктегі түзулердің | | параллель түзулерді анықтайды; | 1 | |||||
| өзара | орналасуын | | параллель түзулердің белгісін жазады; | 1 | ||||
| анықтайды | | | | қиылысатын түзулерді табады; | | 1 | ||
| | | | | | | | | |
| | | | | | | | | |
| | | | 2 | қиылысатын | түзулердің | қиылысу | 1 | |
| | | | | нүктелерін табады; | | |||
| | | | | | | |||
| | | | | айқас түзулерді табады; | | 1 | ||
| | | | | | | |||
| | | | | айқас түзулердің белгісін жазады; | 1 | |||
| | | | | |||||
| Түзу мен жазықтықтың | | түзулердің параллельділігін анықтайды; | 1 | |||||
| параллельдік | белгісін | 3 | түзу | мен | жазықтықтың параллельдік | 1 | ||
| қолданады | | | белгісін қолданады; | | ||||
| | | | | |||||
| | | | | ұзындықты анықтайды; | | 1 | ||
| | | | | | | | | |
| | | | | | | |||
| Жазықтықтардың | | параллель | жазықтықтардың | қасиетін | 1 | |||
| параллельдік | қасиетін | | қолданады; | | | |||
| | | | | |||||
| қолданады | | | 4 | үшбұрыштардың ұқсастығын | анықтап, | | ||
| | | | сәйкес | қабырғалардың | қатынасын | 1 | ||
| | | | | |||||
| | | | | жазады; | | | | |
| | | | | белгісізді табады. | | 1 | ||
| | | | | | | | | |
| Барлығы: | | | | | | | | 15 |
| | | | | | | | | |
6
Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ______________________________________________________
| | Бағалау критерийі | | | Оқу жетістіктерінің деңгейлері | | | | | |||||
| | | | | Төмен | Орта | | | | Жоғары | | |||
| | | | | | | | | | |||||
| Стеореметрия | аксиомаларын | Стереометрия | аксиомаларын, | Стереометрия | | | Стереометрия | аксиомаларын, | |||||
| және | олардың | салдарын | олардың | | салдарларын | аксиомаларын, | олардың | | олардың | | салдарларын, | ||
| қолданады | | қолдануда қиналады. | салдарларын | | қолдануда | | математикалық символикасын | ||||||
| | | | | | | қателіктер жібереді. | | дұрыс қолданады. | | ||||
| | | | | | | | | ||||||
| Кеңістіктегі түзулердің өзара | Кеңістіктегі | түзулердің өзара | Кеңістіктегі | | параллель/ | | Кеңістіктегі түзулердің өзара | ||||||
| орналасуын анықтайды | орналасуын | анықтауда | айқас/ қиылысатын түзулерді | | орналасуын | | дұрыс | ||||||
| | | | қиналады. | | анықтауда | | қателіктер | | анықтайды. | | | ||
| | | | | | | жібереді. | | | | | | | |
| | | | | | | | | | | | | ||
| Түзу | мен | жазықтықтың | Түзу | мен | жазықтықтың | Түзумен | жазықтықтың | | Түзу | мен | жазықтықтың | ||
| параллельдік | белгісін | параллельдік | белгісін | параллельдік | | белгісін | | параллельдік | белгісін | дұрыс | |||
| қолданады | | қолдануда қиналады. | қолданады, | бірақ | жауапты | | қолданады. | | | ||||
| | | | | | | негіздеуде | | қателіктер | | | | | |
| | | | | | | жібереді. | | | | | | | |
| | | | | | | | | ||||||
| Жазықтықтардың | параллельдік | Жазықтықтардың параллельдік | Жазықтықтардың | | | Жазықтықтардың | | ||||||
| қасиетін қолданады | қасиетін қолдануда қиналады. | параллельдік | | қасиетін | | параллельдік | қасиетін | ||||||
| | | | | | | қолданады, | | бірақ | | қолданып, | есепті | дұрыс | |
| | | | | | | есептеулерде | | қателіктер | | шығарады. | | | |
| | | | | | | жібереді. | | | | | | | |
| | | | | | | | | | | | | | |
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау
Тақырып
Кеңістіктегі түзулер арасындағы бұрыш
Перпендикуляр және көлбеу
Үш перпендикуляр туралы теорема
Оқу мақсаты
10.2.6 Кеңістіктегі екі түзу арасындағы бұрыш
анықтамасын білу
10.3.5 Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын білу
10.3.1 Үш перпендикуляр туралы теореманы білу және
оны есептер шығаруда қолдану
Бағалау критерийі
Білім алушы
Кеңістіктегі екі түзу арасындағы бұрышты
табады
Ойлау дағдыларының
деңгейлері
Орындау уақыты
Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын қолданады
Үш перпендикуляр туралы теореманы
қолданады
Қолдану
25 минут
Тапсырма
-
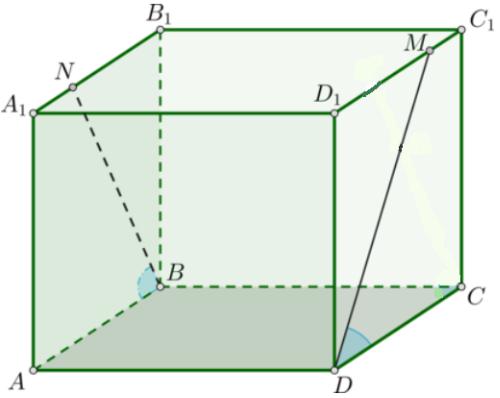
ABCDA1B1C1D1-текше. A1B1және C1D1қырларында сәйкесінше N және M
нүктелері берілген, MDC NBA 600 . NB және MD кесінділері арасындағы бұрышты табыңыз.
-
M нүктесінен жазықтығына MA, MB көлбеулері және MO перпендикуляры жүргізілген.
-
көлбеулердің жазықтығына проекциясын салыңыз;
b) егер = 600, = 450, = 16 см болса, проекциялардың ұзындығын табыңыз.

-
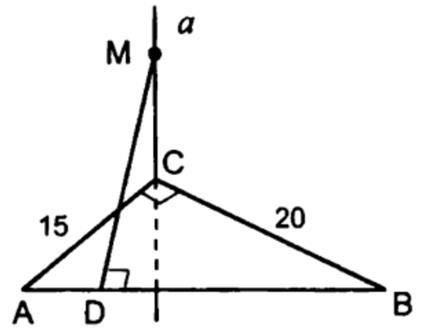
a түзуі ABC жазықтығына перпендикуляр, MD 13см,АС=15см,ВС=20см. АВС үшбұрышы тікбұрышты: = 900.
MC кесіндісінің ұзындығын табыңыз.
9
| Бағалау критерийі | Тапсырма | | Дескриптор | | Балл | ||
| № | | Білім алушы | | ||||
| | | | | | | ||
| Кеңістіктегі | екі түзу | | NB немесеMDтүзуін екінші түзумен | 1 | |||
| арасындағы | бұрышты | 1 | қиылысқанша параллель көшіреді; | | |||
| табады | | | | | | | |
| | | NB жәнеMDкесінділері арасындағы | 1 | ||||
| | | | |||||
| | | | | бұрышты анықтайды; | | | |
| Кеңістіктегі | | 2a | көлбеулердің проекцияларын салады | 1 | |||
| перпендикуляр, көлбеу | | бұрыштың | тангенсінің | анықтамасын | 1 | ||
| және | | көлбеудің | | қолданады; | | ||
| | | | | ||||
| проекциясы | | 2b | теңбүйірлі | тікбұрышты | үшбұрыштың | 1 | |
| анықтамаларын | | қасиетін қолданады; | | ||||
| | | | |||||
| қолданады | | | проекциялардың ұзындықтарын табады; | 1 | |||
| | | | | | | | |
| Үш | перпендикуляр | | ∆ABC | тікбұрышты | үшбұрышына | 1 | |
| туралы | | теореманы | | Пифагор теоремасын қолданады; | |||
| | | | |||||
| қолданады | | | гипотенуза ұзындығын есептейді; | 1 | |||
| | | | | | | ||
| | | | 3 | үш перпендикуляр туралы теореманы | 1 | ||
| | | | қолданады; | | |||
| | | | | | | ||
| | | | | үшбұрыштың тік бұрышынан түсірілген | 1 | ||
| | | | | биіктіктің ұзындығын табады; | |||
| | | | | | |||
| | | | | | | ||
| | | | | ізделінді кесінді ұзындығын табады; | 1 | ||
| | | | | | | | |
| Барлығы: | | | | | | 11 | |
| | | | | | | | |