Файл: Уметь пользоваться современной научной аппаратурой для проведения инженерных измерений и научных исследований использовать основные приемы обработки экспериментальных данных владеть.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х.
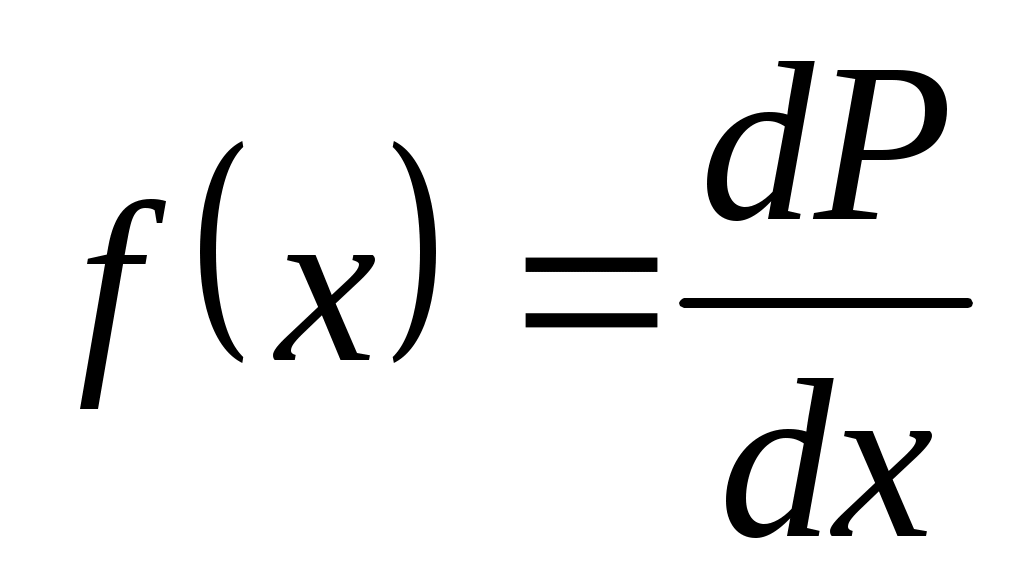 .
.
Зная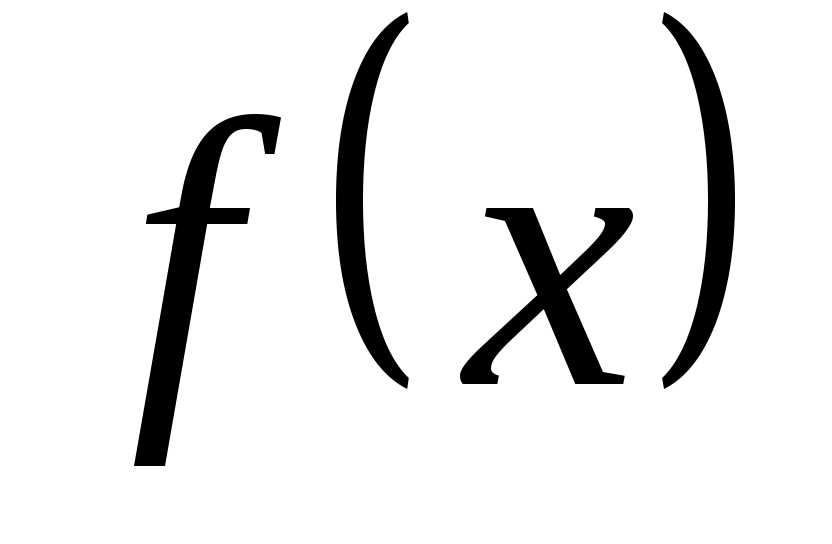 , можно определить вероятность того, что непрерывная случайная величина будет иметь значение в интервале от
, можно определить вероятность того, что непрерывная случайная величина будет иметь значение в интервале от 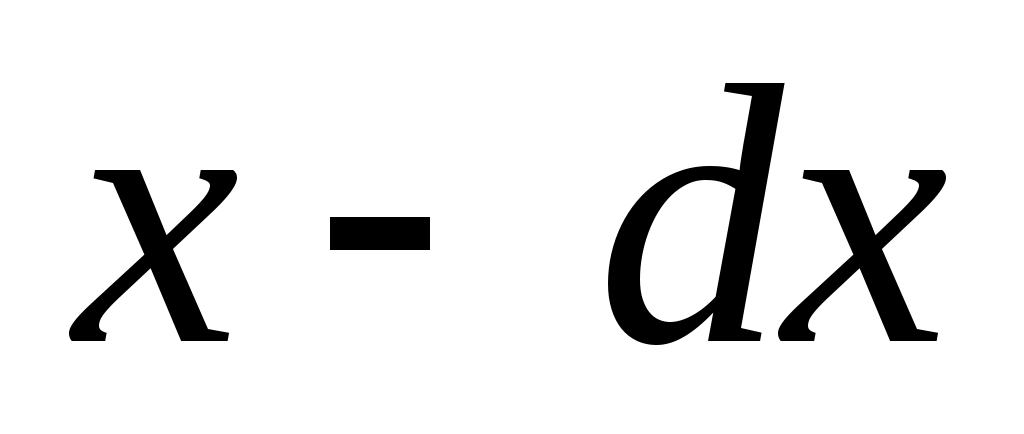 до
до 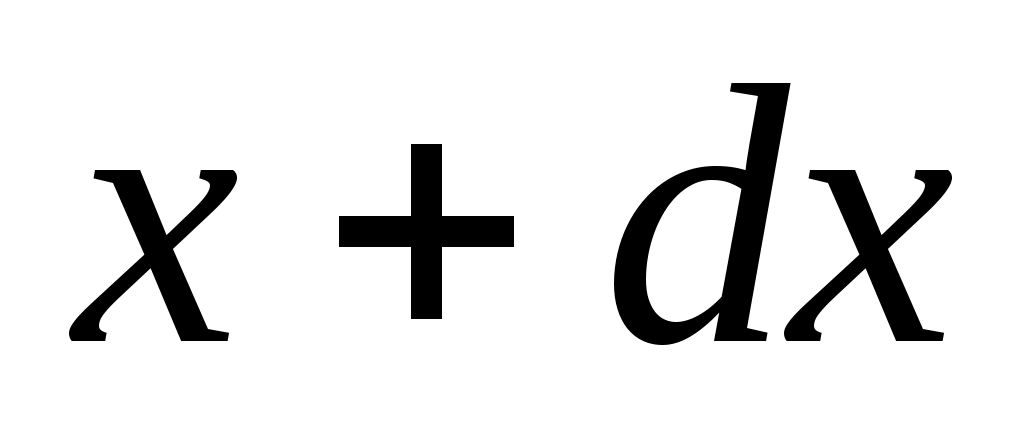 .
.
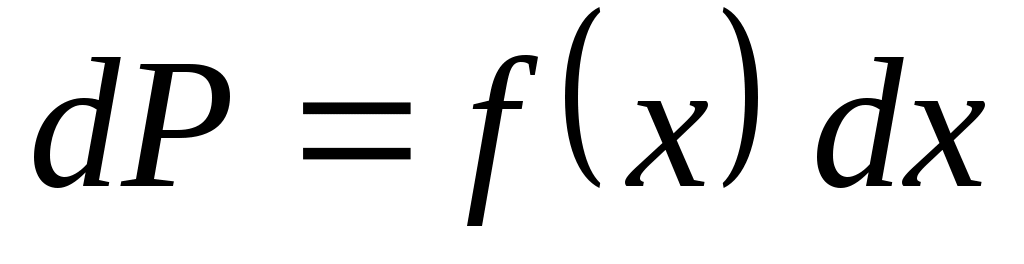 .
.
Кривая нормального распределения и ее физический смысл
В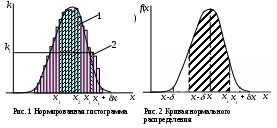 лабораторном эксперименте проведено n измерений одной и той же физической величины и получены ее значения х1, х2, х3,...хn. Отложив эти значения в виде точек на оси абсцисс (рис.1), получим на этой оси множество точек (если число измерений достаточно велико), причем их плотность в одних местах будет больше, в других меньше. Выделим на оси абсцисс равные интервалы Δx = , и сосчитаем, сколько точек попало в каждый интервал. Построив над каждым интервалом прямоугольник с высотой, равной количеству точек в данном интервале, получим ступенчатую кривую (гистограмму).
лабораторном эксперименте проведено n измерений одной и той же физической величины и получены ее значения х1, х2, х3,...хn. Отложив эти значения в виде точек на оси абсцисс (рис.1), получим на этой оси множество точек (если число измерений достаточно велико), причем их плотность в одних местах будет больше, в других меньше. Выделим на оси абсцисс равные интервалы Δx = , и сосчитаем, сколько точек попало в каждый интервал. Построив над каждым интервалом прямоугольник с высотой, равной количеству точек в данном интервале, получим ступенчатую кривую (гистограмму).
Например, в выделенный интервал, заключенный между значениями хi и хi + , попало ki точек и высота прямоугольника 1 равна ki.
Отношение площади выделенного прямоугольника к площади всех прямоугольников, т.е. ki/[(k1 + k2+ ... + kn)] = ki/n = ki/n, определяет вероятность того, что при проведении единичного измерения его результат окажется в интервале между хi и xi + .
Гистограмму строят так, чтобы сумма площадей всех прямоугольников была равна единице (такая процедура называется нормировкой). Тогда вероятность попадания результата измерения в интервале от х1 до х2 равна суммарной площади прямоугольников, заключенных между х1 и х2.
Если неограниченно увеличивать число измерений n, а интервал устремить к нулю, то в пределе нормированная гистограмма перейдет в непрерывную кривую (рис.2), которую называют кривой нормального распределения. Функция распределения определяется формулой Гаусса
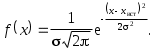
Физический смысл остается тем же: площадь под любым участком кривой нормального распределения равна вероятности «попадания» результата измерения в интервал х, ограниченный этим участком.
Входящую в формулу Гаусса величину называют стандартным отклонением, а 2 - дисперсией измерения.
При достаточно большом числе измерений стандартное отклонение (или средняя квадратичная ошибка) определяется по формуле
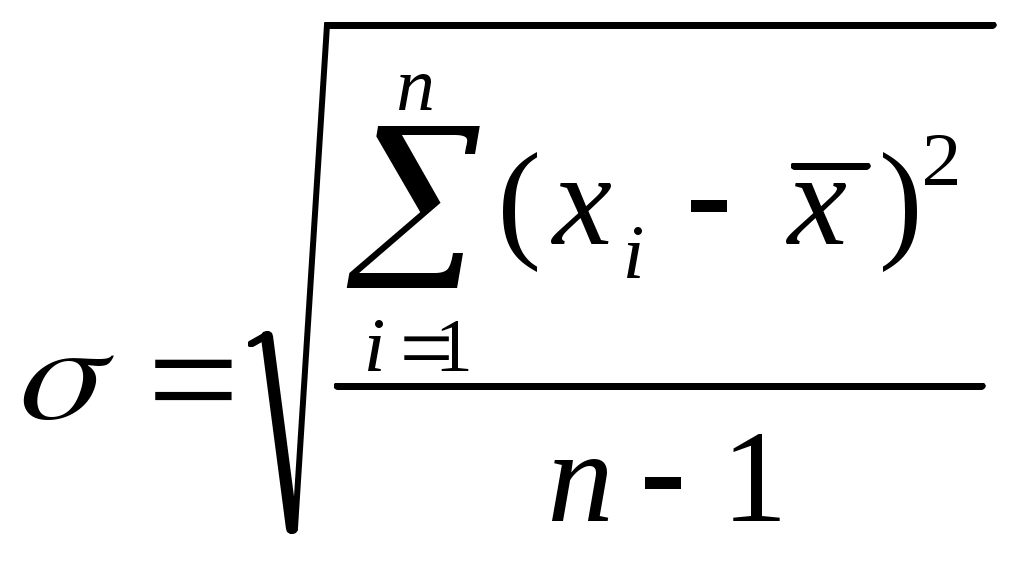
Средняя квадратичная ошибка используется, когда необходимо знать надежность полученных результатов.
В случае выполнения серии измерений, необходимо рассчитать средние арифметические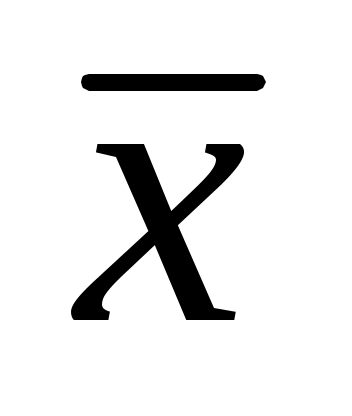 каждого отдельного измерения и их средние квадратичные погрешности , а затем определить среднюю квадратичную погрешность серии независимых прямых измерений одной и той же величины
каждого отдельного измерения и их средние квадратичные погрешности , а затем определить среднюю квадратичную погрешность серии независимых прямых измерений одной и той же величины 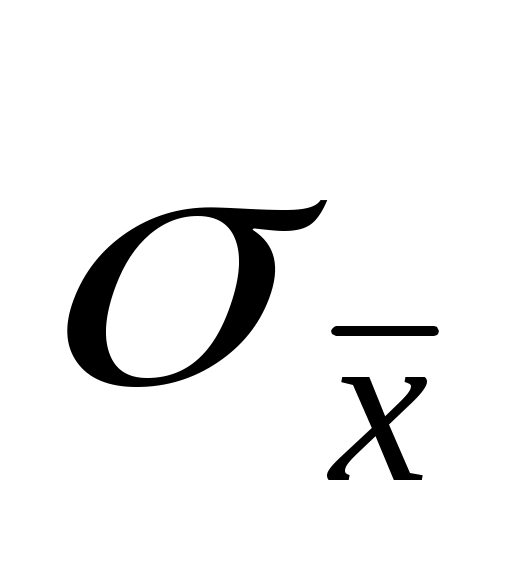 по формуле
по формуле
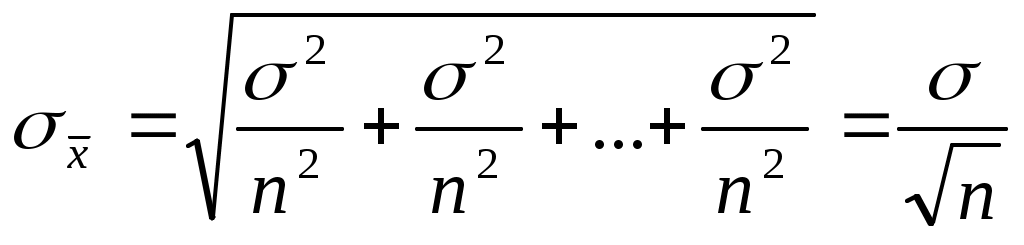
или средняя квадратичная ошибка среднего значения
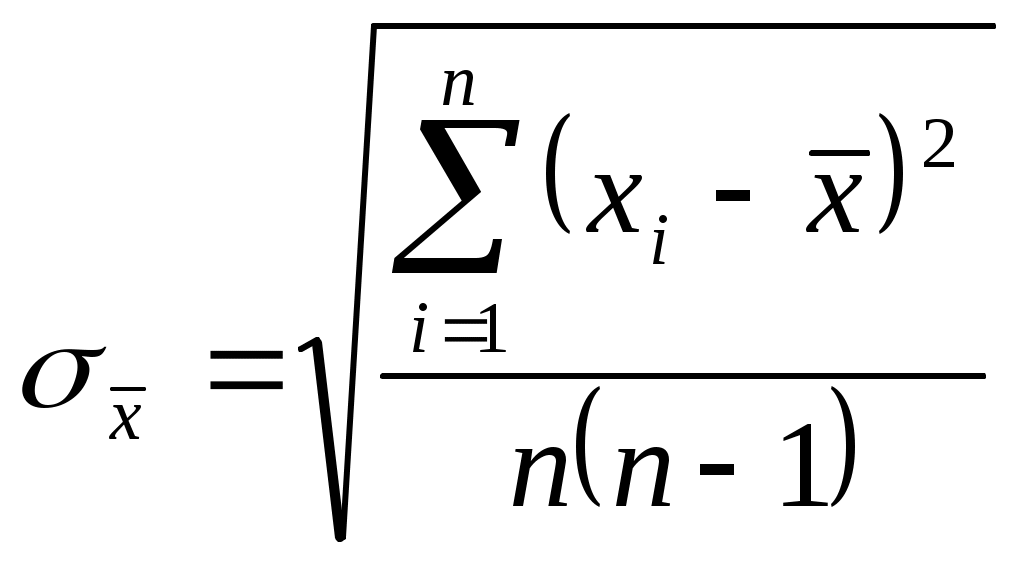
где: - средняя квадратичная ошибка каждого отдельного измерения, n – число измерений.
При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).
Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки.
Физический смысл средней квадратичной погрешности.
При любых численных значениях стандартного отклонения для доверительного интервала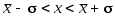 (рис.2) доверительная вероятность всегда равна 0,68. То есть можно утверждать, что с вероятностью 68 % результат единичного измерения окажется в интервале от
(рис.2) доверительная вероятность всегда равна 0,68. То есть можно утверждать, что с вероятностью 68 % результат единичного измерения окажется в интервале от 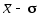 до
до 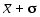 или, что то же самое, с вероятностью 68 % ошибка единичного измерения не превышает величины стандартного отклонения (среднеквадратичной погрешности).
или, что то же самое, с вероятностью 68 % ошибка единичного измерения не превышает величины стандартного отклонения (среднеквадратичной погрешности).
Доверительному интервалу от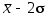 до
до 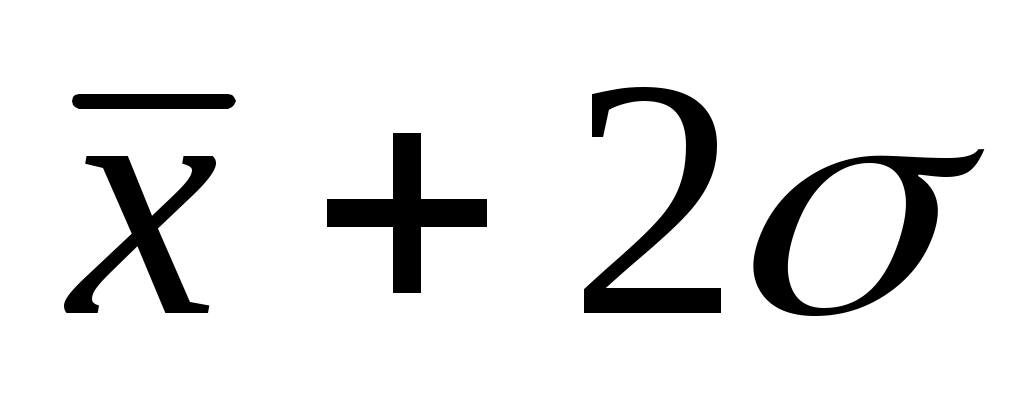 соответствует доверительная вероятность 95 %, а доверительному интервалу от
соответствует доверительная вероятность 95 %, а доверительному интервалу от 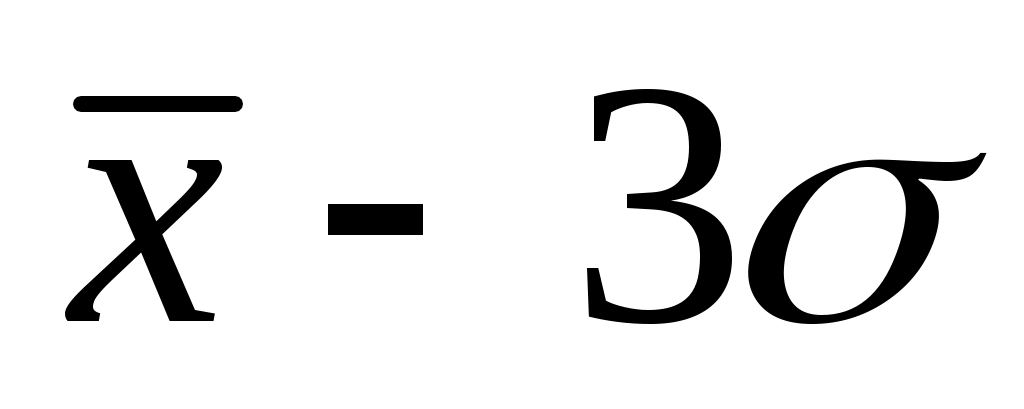 до
до 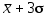 - доверительная вероятность 99,7 %.
- доверительная вероятность 99,7 %.
Если ограничится доверительной вероятностью 68 %, то величину стандартного отклонения используют для оценки случайной погрешности. При этом результат измерений величины х должен быть представлен в виде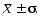 Эта запись означает, что с вероятностью 68 % результат единичного измерения величины х окажется в интервале значений от (
Эта запись означает, что с вероятностью 68 % результат единичного измерения величины х окажется в интервале значений от (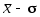 ) до (
) до (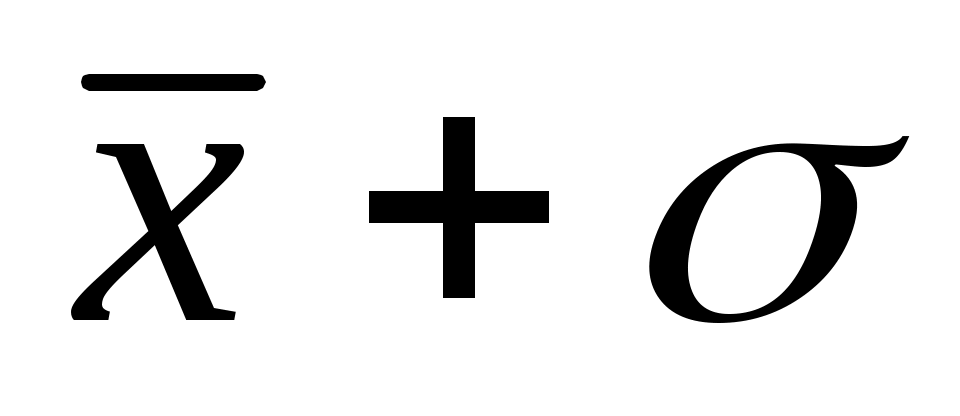 ).
).
Учет систематических ошибок
Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.
Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. У неэлектрических приборов, имеющих шкалу с делениями, принимают в качестве систематической ошибки половину цены деления прибора. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм. Приборы, имеющие дополнительную шкалу (нониус), имеют точность измерений, соответствующую дополнительной шкале. Например, для измерений штангенциркулем – 0,1–0,05 мм; микрометром – 0,01 мм.
На шкалах электроизмерительных приборов указывается класс точности. Согласно ГОСТу, электроизмерительные приборы делятся по степени точности на семь классов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆х по формуле
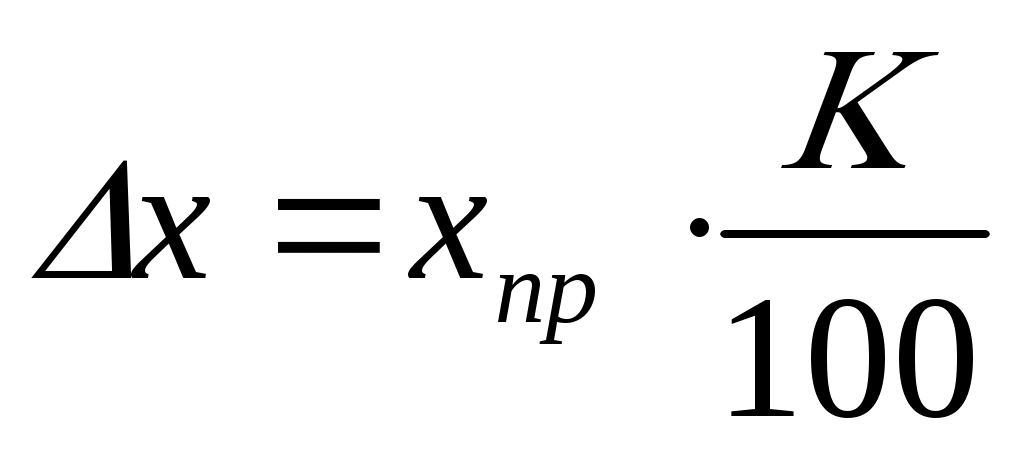
где К – класс точности прибора в процентах, xпр – предельное значение величины, которое может быть измерено по шкале прибора.
Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более
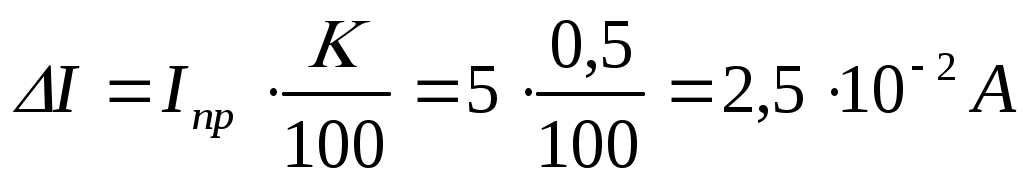
Среднее значение полной погрешности складывается из
случайной и систематической погрешности
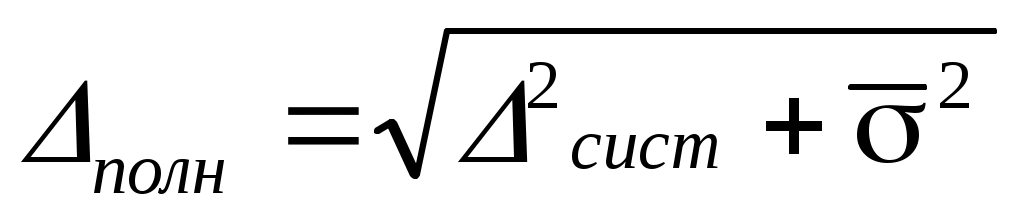
Ответ с учетом систематических и случайных ошибок записывается в виде
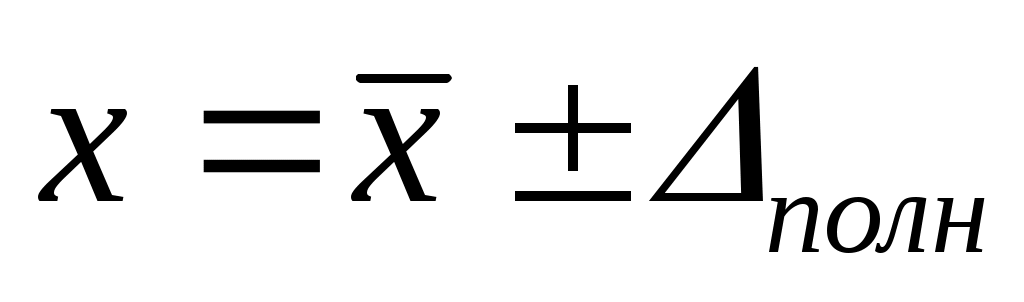
Погрешность косвенного измерения
Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными.
Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку косвенных измерений.
Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.
Пусть физическая величина (x, y, z, ...) является функцией ряда независимых аргументов x, y, z, ..., каждый из которых может быть определен экспериментально. Путем прямых измерений определяются величины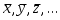 и оцениваются их средние абсолютные погрешности
и оцениваются их средние абсолютные погрешности 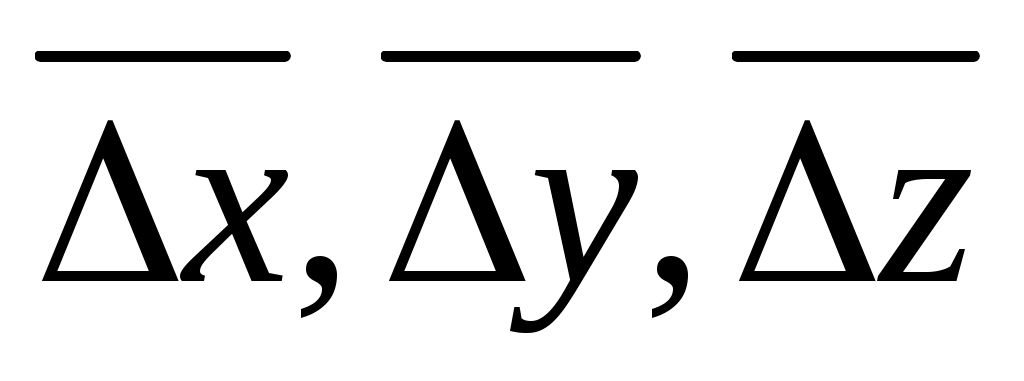 или средние квадратичные погрешности
или средние квадратичные погрешности 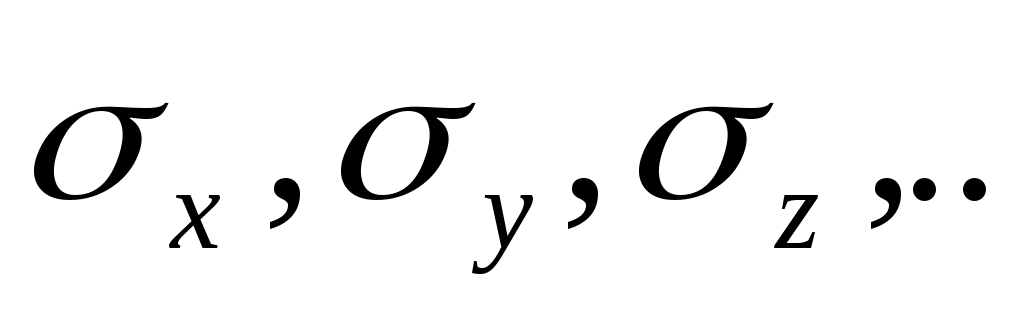 .
.
Средняя абсолютная погрешность косвенных измерений физической величины вычисляется по формуле
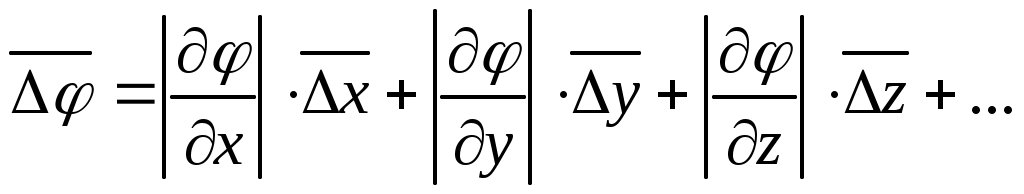
где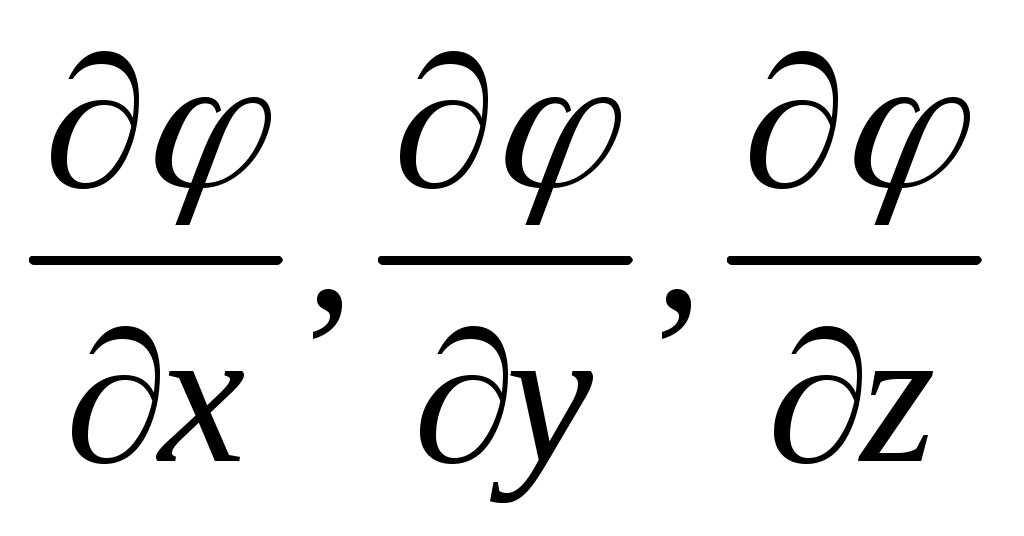 - частные производные от φ поx, y, z, вычисленные для средних значений соответствующих аргументов.
- частные производные от φ поx, y, z, вычисленные для средних значений соответствующих аргументов.
Так как в формуле использованы абсолютные величины всех членов суммы, то выражение для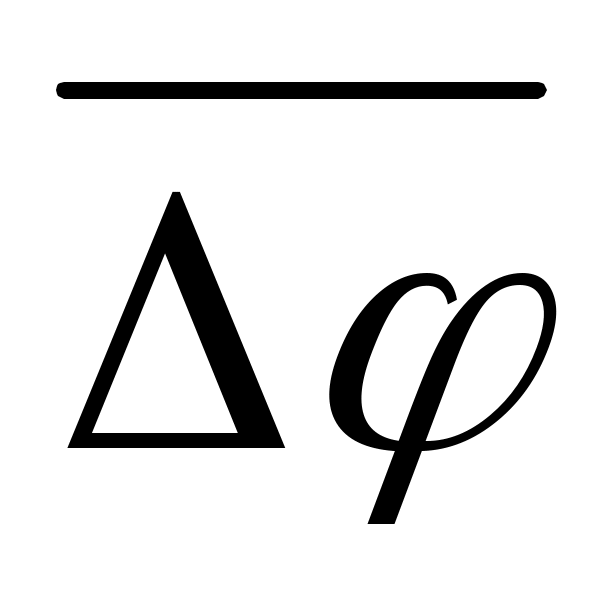 оценивает максимальную погрешность измерения функции при заданных максимальных ошибках независимых переменных.
оценивает максимальную погрешность измерения функции при заданных максимальных ошибках независимых переменных.
Средняя квадратичная погрешность косвенных измерений физической величины
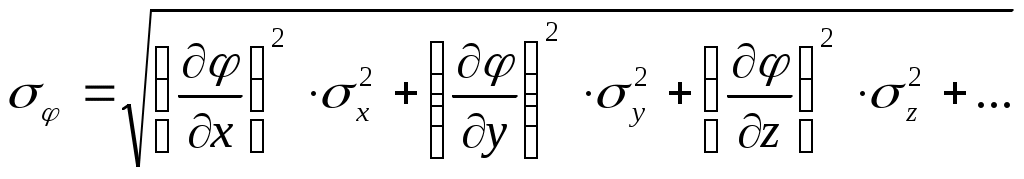
Относительная максимальная погрешность косвенных измерений физической величины
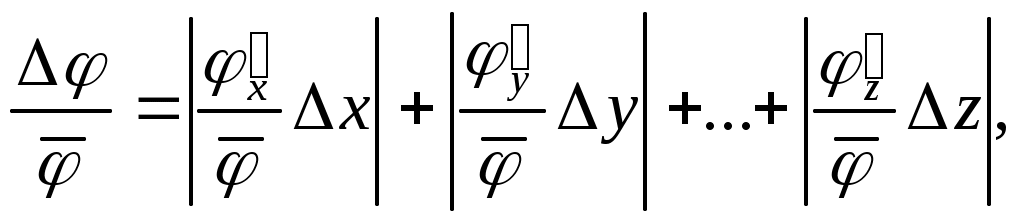
где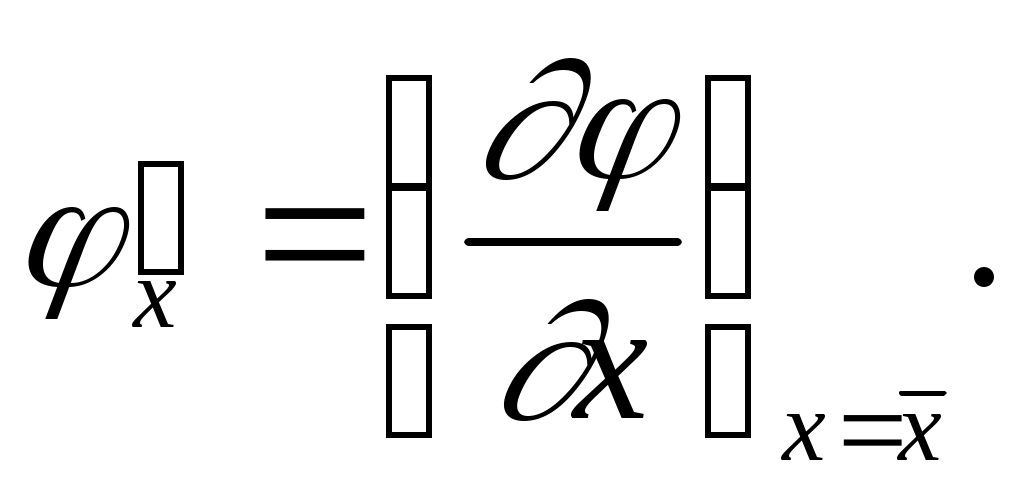
и т. д.
Аналогично можно записать относительную среднюю квадратичную погрешность косвенных измерений
Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять максимальную относительную погрешность косвенных измерений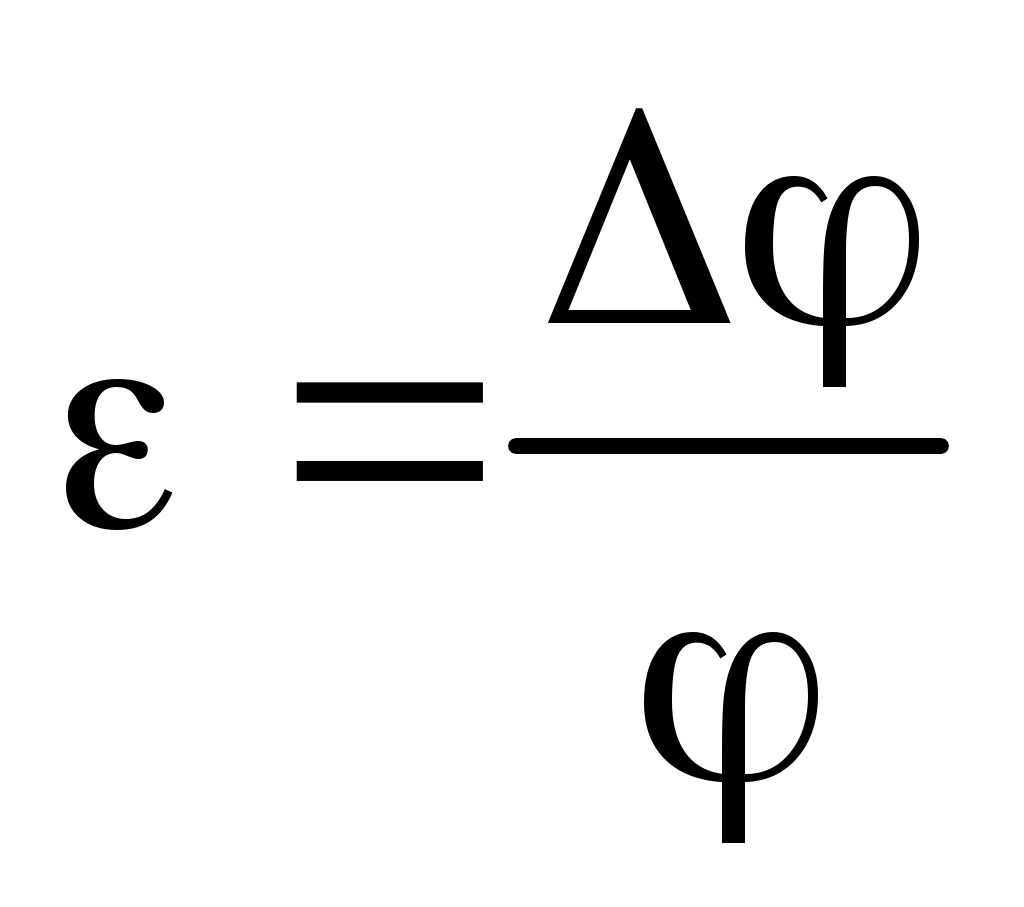 . Для этого (в случае средней абсолютной погрешности) надо проделать следующее.
. Для этого (в случае средней абсолютной погрешности) надо проделать следующее.
1. Прологарифмировать выражение для косвенного измерения физической величины.
2. Продифференцировать полученное выражение.
3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.
4. Взять выражение перед различными дифференциалами по модулю (в соответствии с теорией Гаусса погрешности складываются по абсолютной величине).
5. Формально заменить значки дифференциалов на значки абсолютной погрешности .
Затем, зная , можно вычислить абсолютную погрешность по формуле
=
Пример 1. Вывод формулы для вычисления максимальной относительной погрешности косвенных измерений объёма цилиндра.
Выражение для косвенного измерения физической величины (исходная формула)
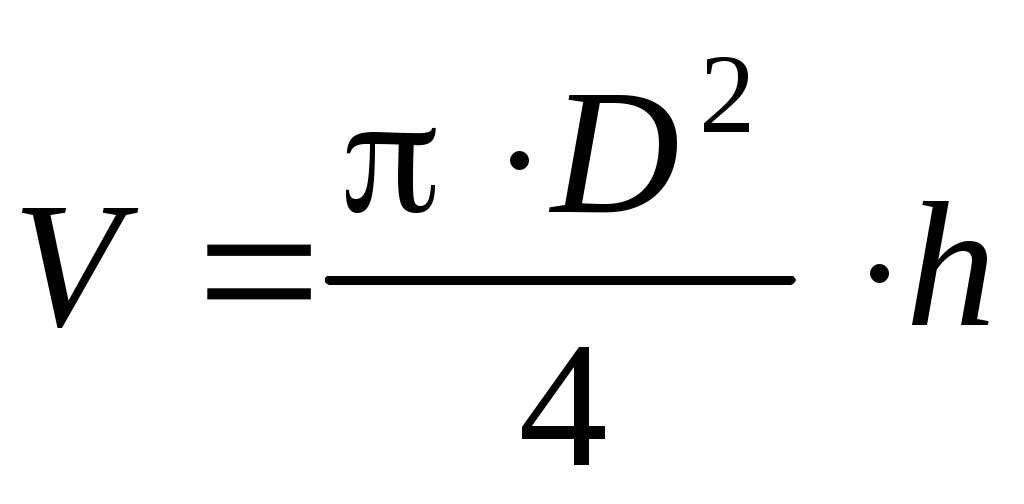
Величина диаметра D и высоты цилиндра h измеряются непосредственно приборами с погрешностями прямых измерений соответственно D и h.
Прологарифмируем исходную формулу и получим
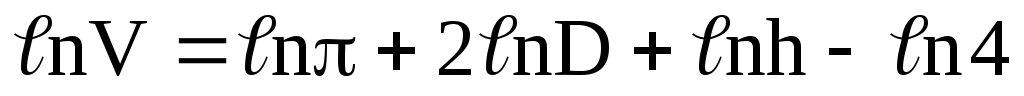
Продифференцируем полученное уравнение
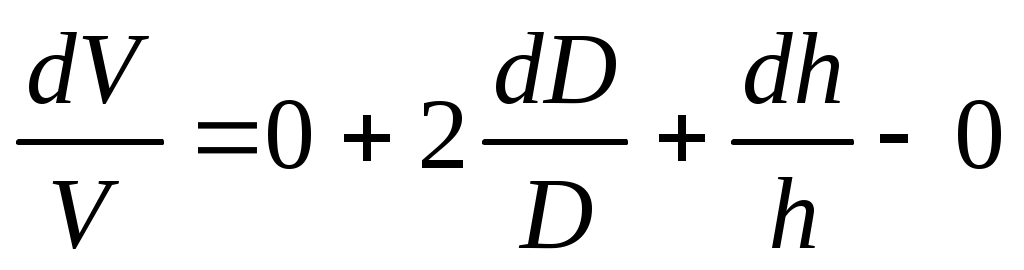
Заменив значки дифференциалов на значки абсолютной погрешности , окончательно получим формулу для расчёта максимальной относительной погрешности косвенных измерений объёма цилиндра
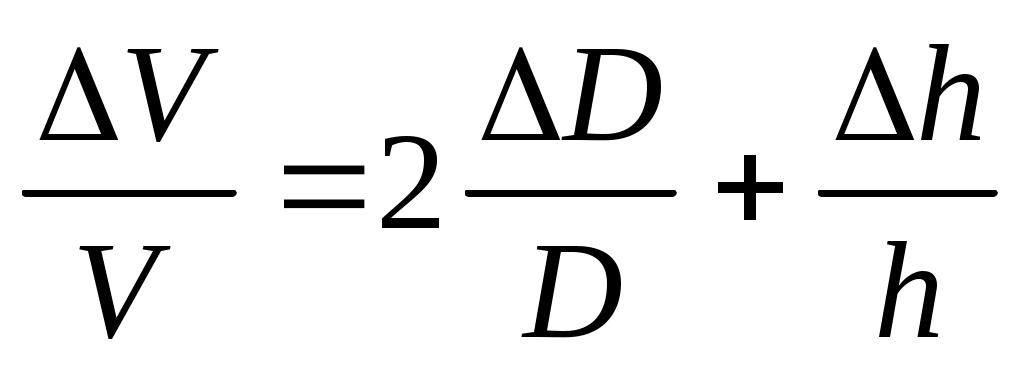
правильно – = 0,04,
неправильно – = 0,0382.
Зная
Кривая нормального распределения и ее физический смысл
В
 лабораторном эксперименте проведено n измерений одной и той же физической величины и получены ее значения х1, х2, х3,...хn. Отложив эти значения в виде точек на оси абсцисс (рис.1), получим на этой оси множество точек (если число измерений достаточно велико), причем их плотность в одних местах будет больше, в других меньше. Выделим на оси абсцисс равные интервалы Δx = , и сосчитаем, сколько точек попало в каждый интервал. Построив над каждым интервалом прямоугольник с высотой, равной количеству точек в данном интервале, получим ступенчатую кривую (гистограмму).
лабораторном эксперименте проведено n измерений одной и той же физической величины и получены ее значения х1, х2, х3,...хn. Отложив эти значения в виде точек на оси абсцисс (рис.1), получим на этой оси множество точек (если число измерений достаточно велико), причем их плотность в одних местах будет больше, в других меньше. Выделим на оси абсцисс равные интервалы Δx = , и сосчитаем, сколько точек попало в каждый интервал. Построив над каждым интервалом прямоугольник с высотой, равной количеству точек в данном интервале, получим ступенчатую кривую (гистограмму). Например, в выделенный интервал, заключенный между значениями хi и хi + , попало ki точек и высота прямоугольника 1 равна ki.
Отношение площади выделенного прямоугольника к площади всех прямоугольников, т.е. ki/[(k1 + k2+ ... + kn)] = ki/n = ki/n, определяет вероятность того, что при проведении единичного измерения его результат окажется в интервале между хi и xi + .
Гистограмму строят так, чтобы сумма площадей всех прямоугольников была равна единице (такая процедура называется нормировкой). Тогда вероятность попадания результата измерения в интервале от х1 до х2 равна суммарной площади прямоугольников, заключенных между х1 и х2.
Если неограниченно увеличивать число измерений n, а интервал устремить к нулю, то в пределе нормированная гистограмма перейдет в непрерывную кривую (рис.2), которую называют кривой нормального распределения. Функция распределения определяется формулой Гаусса
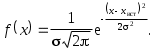
Физический смысл остается тем же: площадь под любым участком кривой нормального распределения равна вероятности «попадания» результата измерения в интервал х, ограниченный этим участком.
Входящую в формулу Гаусса величину называют стандартным отклонением, а 2 - дисперсией измерения.
При достаточно большом числе измерений стандартное отклонение (или средняя квадратичная ошибка) определяется по формуле
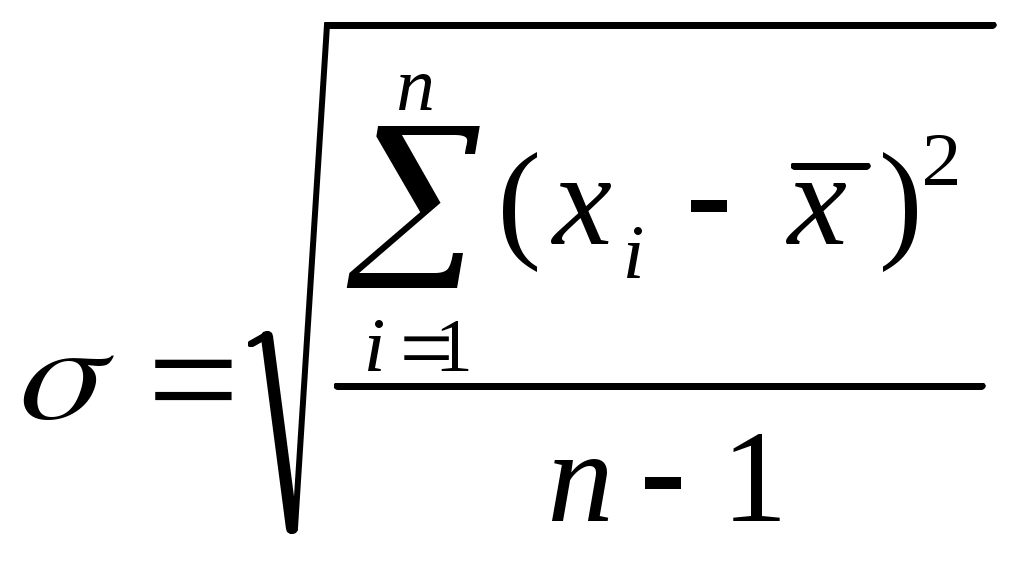
Средняя квадратичная ошибка используется, когда необходимо знать надежность полученных результатов.
В случае выполнения серии измерений, необходимо рассчитать средние арифметические
или средняя квадратичная ошибка среднего значения
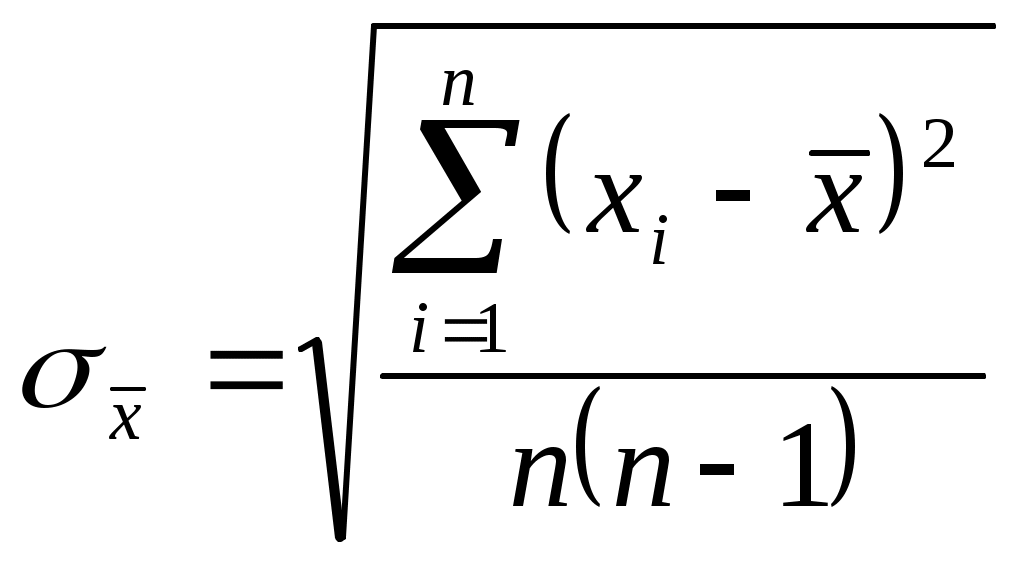
где: - средняя квадратичная ошибка каждого отдельного измерения, n – число измерений.
При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).
Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки.
Физический смысл средней квадратичной погрешности.
При любых численных значениях стандартного отклонения для доверительного интервала
Доверительному интервалу от
Если ограничится доверительной вероятностью 68 %, то величину стандартного отклонения используют для оценки случайной погрешности. При этом результат измерений величины х должен быть представлен в виде
Учет систематических ошибок
Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.
Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. У неэлектрических приборов, имеющих шкалу с делениями, принимают в качестве систематической ошибки половину цены деления прибора. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм. Приборы, имеющие дополнительную шкалу (нониус), имеют точность измерений, соответствующую дополнительной шкале. Например, для измерений штангенциркулем – 0,1–0,05 мм; микрометром – 0,01 мм.
На шкалах электроизмерительных приборов указывается класс точности. Согласно ГОСТу, электроизмерительные приборы делятся по степени точности на семь классов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆х по формуле
где К – класс точности прибора в процентах, xпр – предельное значение величины, которое может быть измерено по шкале прибора.
Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более
Среднее значение полной погрешности складывается из
случайной и систематической погрешности
Ответ с учетом систематических и случайных ошибок записывается в виде
Погрешность косвенного измерения
Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными.
Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку косвенных измерений.
Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.
Пусть физическая величина (x, y, z, ...) является функцией ряда независимых аргументов x, y, z, ..., каждый из которых может быть определен экспериментально. Путем прямых измерений определяются величины
Средняя абсолютная погрешность косвенных измерений физической величины вычисляется по формуле
где
Так как в формуле использованы абсолютные величины всех членов суммы, то выражение для
Средняя квадратичная погрешность косвенных измерений физической величины
Относительная максимальная погрешность косвенных измерений физической величины
где
и т. д.
Аналогично можно записать относительную среднюю квадратичную погрешность косвенных измерений
Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять максимальную относительную погрешность косвенных измерений
1. Прологарифмировать выражение для косвенного измерения физической величины.
2. Продифференцировать полученное выражение.
3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.
4. Взять выражение перед различными дифференциалами по модулю (в соответствии с теорией Гаусса погрешности складываются по абсолютной величине).
5. Формально заменить значки дифференциалов на значки абсолютной погрешности .
Затем, зная , можно вычислить абсолютную погрешность по формуле
=
Пример 1. Вывод формулы для вычисления максимальной относительной погрешности косвенных измерений объёма цилиндра.
Выражение для косвенного измерения физической величины (исходная формула)
Величина диаметра D и высоты цилиндра h измеряются непосредственно приборами с погрешностями прямых измерений соответственно D и h.
Прологарифмируем исходную формулу и получим
Продифференцируем полученное уравнение
Заменив значки дифференциалов на значки абсолютной погрешности , окончательно получим формулу для расчёта максимальной относительной погрешности косвенных измерений объёма цилиндра
4. Правила представления результатов измерения
-
Результаты измерения принято представлять в виде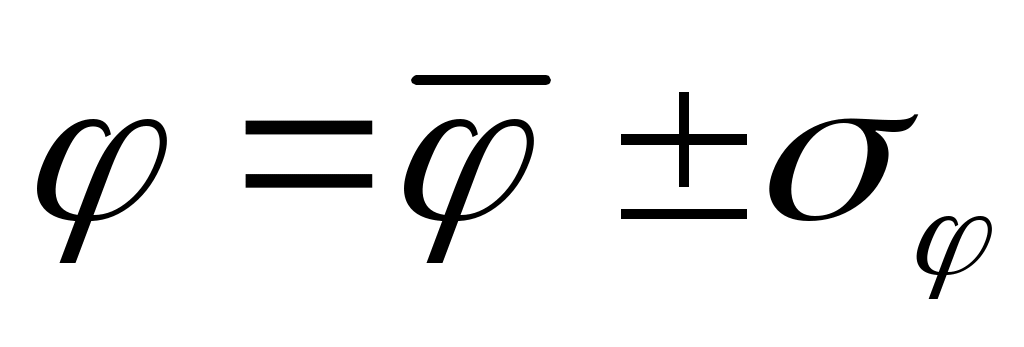 или
или 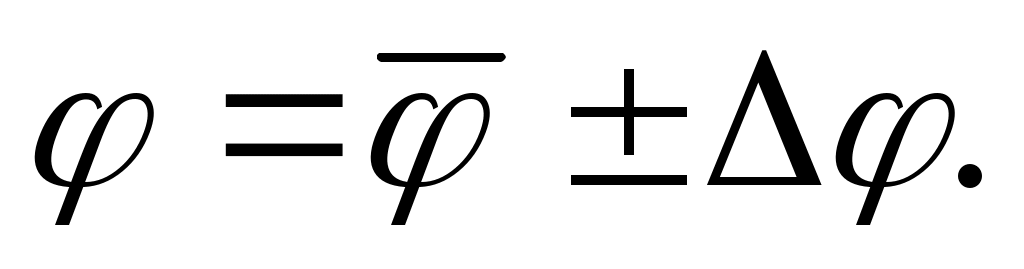
-
Погрешность должна округляться до одной значащей цифры:
правильно – = 0,04,
неправильно – = 0,0382.
-
Последняя значащая цифра результата должна быть того же порядка величины, что и погрешность: