Файл: Уметь пользоваться современной научной аппаратурой для проведения инженерных измерений и научных исследований использовать основные приемы обработки экспериментальных данных владеть.doc

правильно –  = 9,830,03,

неправильно –  = 9,8260,03.

• 
  Если результат имеет очень большую или очень малую величину, необходимо использовать показательную форму записи - одну и ту же для результата и его погрешности, причем запятая десятичной дроби должна следовать за первой значащей цифрой результата:
  

правильно –  = (5,270,03)10^-5,

неправильно –  = 0,00005270,0000003.

• 
  Если результат имеет размерность, ее необходимо указать:
  

правильно – g = (9,820,02) м/c²,

неправильно – g = (9,820,02).

5. Правила построения графиков

1. Графики строятся с использованием компьютера.

2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х), значения функции - на оси ординат (ось у).

3. Из экспериментальных данных определить пределы изменения аргумента и функции.

4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин.

5. На осях координат указать масштаб (при очень больших или очень малых величинах, показательную часть в записи величины указать рядом с единицами измерений на оси).

6. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой).

7. Провести через экспериментальные точки плавную линию, в соответствии с выбранным законом аппроксимации экспериментальных данных, по методу наименьших квадратов.

6. Содержание отчета

Отчёт оформляется в печатном виде на листах формата А4 в соответствии с требованиями, предъявляемыми кафедрой ОТФ, в котором помимо стандартного титульного листа должны быть раскрыты следующие пункты:

1. 
   Цель работы.
   
2. 
   Краткое теоретическое содержание.
   

1. 
   Явление, изучаемое в работе.
   
2. 
   Определение основных физических понятий, объектов, процессов и величин.
   
3. 
   Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчётные формулы.
   
4. 
   Пояснения к физическим величинам и их единицы измерений.
   

3. 
   Схема установки.
   
4. 
   Расчётные формулы.
   
5. 
   Формулы погрешностей косвенных измерений.
   
6. 
   Таблицы с результатами измерений и вычислений. (Таблицы должны иметь номер и название. Единицы измерения физических величин должны быть указаны в отдельной строке.)
   
7. 
   Пример вычисления (для одного опыта).
   

---

1. 
   Исходные данные.
   
2. 
   Вычисления.
   
3. 
   Окончательный результат.
   

8. 
   Графический материал.
   

1. 
   Аналитическое выражение функциональной зависимости, которую необходимо построить.
   
2. 
   На осях координат указать масштаб, физические величины и единицы измерения.
   
3. 
   На координатной плоскости должны быть нанесены экспериментальные точки.
   
4. 
   По результатам эксперимента, представленным на координатной плоскости, провести плавную линию, аппроксимирующую функциональную теоретическую зависимость в соответствии с методом наименьших квадратов.
   

9. 
   Анализ полученного результата. Выводы.
   

ПРИЛОЖЕНИЕ 2

Метод наименьших квадратов
Суть метода заключается в поиске такой функциональной зависимости у = (х, с₁, с₂, ..., с_m) с коэффициентами с_j(j = 1,2,...,m), при которой сумма

                      (1)

будет минимальна. Здесь у_i - совокупность экспериментальных значений функции.

В соответствии с необходимым условием экстремума функций нескольких переменных, нужно приравнять к нулю частные производные суммы (1) по каждому из коэффициентов, т.е.

                  (2)

Полученные уравнения (2) для нахождения коэффициентов с_j называются нормальными уравнениями для выбора наилучшего приближения к экспериментальным данным.

Если аппроксимирующая функция может быть представлена в виде линейной комбинации функций



(здесь _j(x) - известные функции), то аппроксимация называется линейной.

Рассмотрим использование метода на примере наиболее простой, линейной зависимости. Если две переменные у и х связаны зависимостью типа у = А + Вх, то график такой функции, как известно, представляет собой прямую, наклон которой к оси абсцисс определяется коэффициентом В = tg, а точка пересечения ординаты .

На практике каждое измерение х_i и

---

у_i сопровождается погрешностью. На рис. показаны экспериментальные точки с учетом погрешности при наличии линейной зависимости.

Можно провести множество прямых, которые близко проходят около этих точек. Метод наименьших квадратов позволяет подобрать такие коэффициенты А и В, что аппроксимация экспериментальных точек прямой у = f(х, А, В) будет наилучшей с точки зрения выполнения условия (1). Это условие предполагает в качестве критерия наилучших значений А и В такие, при которых вероятность получения всего данного набора результатов измерений у_i(i = 1,2,...,N) максимальна.

Предположим, что результат измерения каждого значения у_i подчиняется распределению Гаусса и средняя квадратическая погрешность _у одинакова для всех измерений. Согласно теории вероятности, вероятность получения значения у_i

, (3)

где y_i = A + Bx_i - истинное значение измеряемой величины при значении аргумента x_i.

Вероятность получения всего набора результатов измерений у₁, у₂, ..., у_N равна произведению соответствующих вероятностей:

… (4)

где



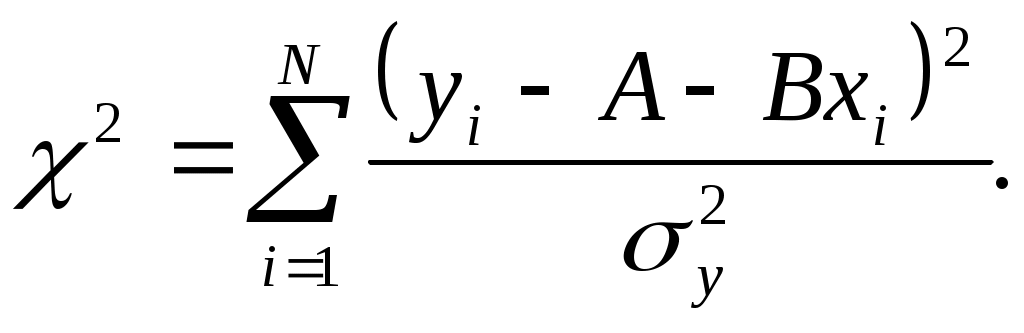
Из формулы (4) следует, что вероятность максимальна, когда значение минимально. Причем, если постоянно для всех y_i, то минимальной должна быть сумма



Итак, мы вернулись к условию (14), введенному в общем виде для любой функциональной зависимости.

Расчет величин А и В. В соответствии с уравнениями (2) приравняем производные по коэффициентам А и В к нулю:



Тогда

---

(5)


 (6)
В результате решения системы нормальных уравнений (5) и (6) получим наилучшие оценки постоянных А и В для прямой у = А + Вх, основанные на измеренных точках x_i, y_i:

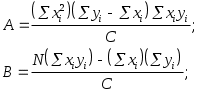(7)

где

Погрешность в измерениях у. Не вдаваясь в довольно сложные теоретические рассуждения, приведем формулу для расчета погрешности _у при наличии линейной аппроксимации у = А +Вх:

(8)

где А и В определяются по формуле (7).

Если в опыте произведено только два измерения, то _у = . Это означает, что при обработке данных опыта методом наименьших квадратов необходимо, чтобы число опытов было по крайней мере больше двух.

Погрешность постоянных А и В. Величины А и В рассчитывают на основании экспериментальных данных x_i и y_i. Так как каждое измерение x_i и y_i сопровождается погрешностью, то и величины А и В имеют погрешности _А и _В. Их рассчитывают по формулам

ПРИЛОЖЕНИЕ 3.

Штангенциркуль

Штангенциркуль предназначен для измерения длины до 150-500 мм, с точностью до 0.1 или 0.05 мм.

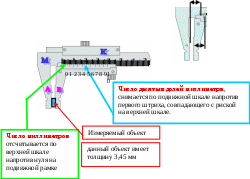
Штангенциркуль состоит из масштабной линейки – М с выступом А, называемым губкой, и подвижной рамки К, с другой губкой В. Рамка передвигается вдоль масштабной линейки, часть рамки снабжена нониусом.

Измеряемый объект зажимается между губками масштабной линейки и рамки.

Нуль масштабной линейки смещен на некоторое расстояние от плоскости губки А, на такое же расстояние смещен и нуль нониуса относительно плоскости губки В на рамке

---

К. Таким образом, измеряемая длина предмета равна расстоянию между нулем масштабной линейки и нулем нониуса.
Снятие отсчета.




Микрометр.

Микрометр используется для измерения небольших значений длины до 25-50 мм и более с точностью до 0.01 мм.

Микрометр состоит из микрометрического винта А, ввинченного в скобу Е.

Измеряемое тело помещается между плоскостями торца А и упора А', укрепленного в скобе.


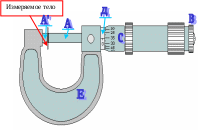
Шаг винта А равен 0,5 мм. На барабане С имеется лимб, разбитый на 50 равных делений. При вращении барабана он переме-щается вдоль шкалы Д, цена деления которой равна 0,5 мм, т.е. шагу винта А. Таким образом, цена деления лимба барабана 0,01 мм.



Измерение микрометром производят следующим образом: вращая винт А за головку В, прижимают измеряемый предмет к упору А' затем берут отсчет по неподвижной шкале Д с точностью до 0,5 мм и прибавляют сотые доли миллиметра, которые отсчитывают по делениям лимба барабана С.

Число сотых отсчитывают по штриху лимба, находящемуся против продольного штриха шкалы Д.

---