Функции нескольких переменных с примерами решения

Функции нескольких переменных:

Многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности введения понятия функции нескольких переменных.

Определение. Пусть имеется 

Например, формула   задает объем цилиндра   как функцию двух переменных:   (радиуса основания) и   (высоты).

Переменные   называются независимыми переменными или аргументами,   — зависимой переменной, а символ   означает закон соответствия. Множество   называется областью определения функции. Очевидно, это подмножество  -мерного пространства.

Пример:

Найти область определения функции:


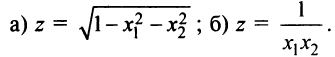
Решение:

а) Область определения задается условием:   или   т.е. представляет собой единичный круг с центром в начале координат.

б) Имеем   т.е. область определения — это плоскость   за исключением координатных прямых   и 

Рассмотрим некоторые примеры функций нескольких переменных.

1. Функция   где  — постоянные числа, называется линейной.

---

 Ее можно рассматривать как сумму   линейных функций от переменных 

2. Функция , — постоянные числа) называется квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т.е. не раскладывается в сумму функций одной переменной.

3. В § 5.6 была определена функция полезности — одно из базовых понятий экономической теории. Многомерный ее аналог — это функция   выражающая полезность от п приобретенных товаров. Чаще всего встречаются следующие ее виды:

 — логарифмическая функция;

 Здесь 
Такая функция называется функцией постоянной эластичности.
Также на случай   переменных обобщается понятие производственной функции (см. § 5.6), выражающей результат производственной деятельности от обусловивших его факторов   Приведем здесь наиболее часто встречающиеся виды производственных функций ( —величина общественного продукта,   — затраты труда,  — объем производственных фондов), полагая для простоты 

а) функция Кобба—Дугласа



б) функция с постоянной эластичностью замещения:

 В настоящей главе мы будем вести изложение в основном для функций двух переменных   при этом практически все понятия и теоремы, сформулированные для 

---

 легко переносятся и на случай   Однако рассмотрение случая двух переменных позволяет использовать наглядную геометрическую иллюстрацию основных понятий настоящей главы.

Функцию двух переменных будем обозначать в дальнейшем  Тогда ее область определения   есть подмножество координатной плоскости 

Окрестностью точки  называется круг, содержащий точку   (см. рис. 15.1).



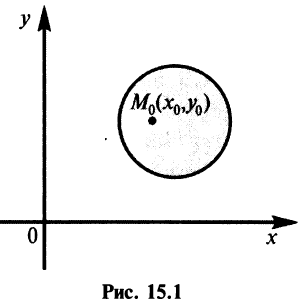
Очевидно, круг на плоскости есть двумерный аналог интервала на прямой.

При изучении функций нескольких переменных во многом используется уже разработанный в предыдущих главах математический аппарат. А именно: любой функции  можно поставить в соответствие пару функций одной переменной: при фиксированном значении   функцию  и при фиксированном значении   функцию 

Следует иметь в виду, что хотя функции   и   имеют одно и то же «происхождение», вид их может существенно различаться. Рассмотрим, например, функцию  , выражающую величину вклада через   лет при ставке 

---

. Очевидно, что это функция степенная по   и показательная по  .

Графиком функции двух переменных   называется множество точек трехмерного пространства   аппликата   которых связана с абсциссой   и ординатой у функционального соотношения  .

График функции двух переменных  , вообще говоря, представляет собой некоторую поверхность в трехмерном пространстве.

Для построения графика функции   полезно рассматривать функции одной переменной   представляющие сечения графика   плоскостями, параллельными координатным плоскостям   т.е. плоскостями

Пример:

Построить график функции 

Решение:

Сечения поверхности   плоскостями, параллельными координатным плоскостям   представляют параболы (например, при   

---

 и т.д.). В сечении поверхности координатной плоскостью   получается окружность   График функции представляет поверхность, называемую параболоидом (см. рис. 15.2). ►



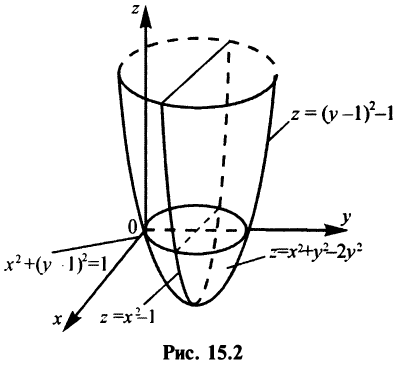
Как видно, график функции двух переменных — значительно более сложный объект, чем график функции одной переменной. Как правило, построение поверхности оказывается довольно трудной задачей. В то же время поверхность в пространстве обладает гораздо меньшей наглядностью, чем линия на плоскости. Поэтому в случае двух переменных для изучения поведения функции желательно использовать другие, более наглядные инструменты. Важнейшим из них являются линии уровня.

Определение._Линией_уровня'>Определение. Линией уровня функции двух переменных   называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно  . Число   в этом случае называется уровнем.



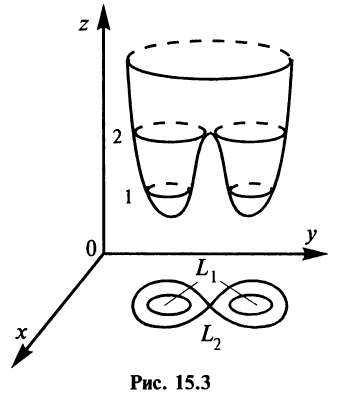
На рис. 15.3 изображены линии уровня, соответствующие значениям  Как видно, линия уровня   состоит из двух непересекающихся кривых. Линия  — самопересекающаяся кривая.

Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм — линий уровня температуры. В § 15.10 мы рассмотрим примеры использования линий уровня функций нескольких переменных в экономическом анализе. Построение линий уровня оказывается существенно более легкой задачей, чем построение графиков самих функций.

Пример:

---

Смотрите также файлы

• Нагревание. Сравнительный анализ устройства и принципов действия теплообменных аппаратов.docx

• 1 Верно Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Show me page.docx

• Программа по повышению эффективности использования дебиторской и кредиторской задолженности в ооо Диалог.docx

• Реферат структурная семейная психотерапия студентка 4 курса Белая Ю. В. Проверил.docx

• Программное обеспечение Soft.docx