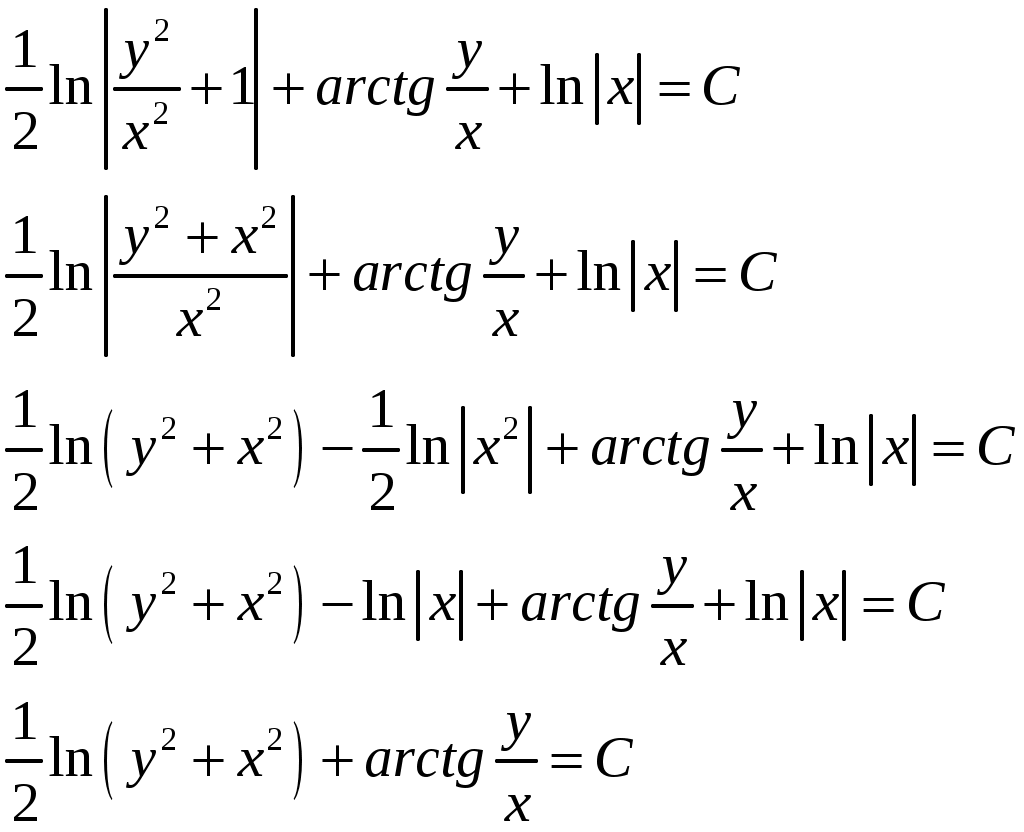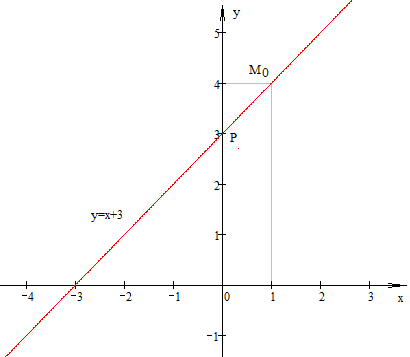
По полученным значениям координат точек построим интегральную кривую.



ЗАДАНИЕ 8. Найдите общее решение дифференциального уравнения первого порядка.

1) .

Решение.

Уравнение имеет вид , следовательно, это линейное дифференциальное уравнение 1-го порядка.

Решение будем искать в виде , тогда .

Подставив в уравнение, получим:



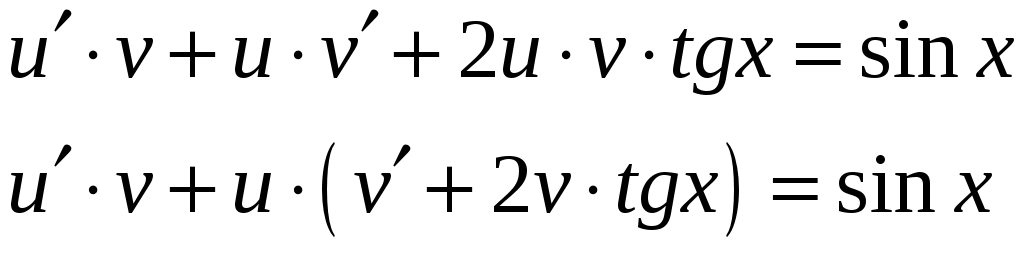
Пусть , тогда .

Получим систему уравнений с разделяющимися переменными:



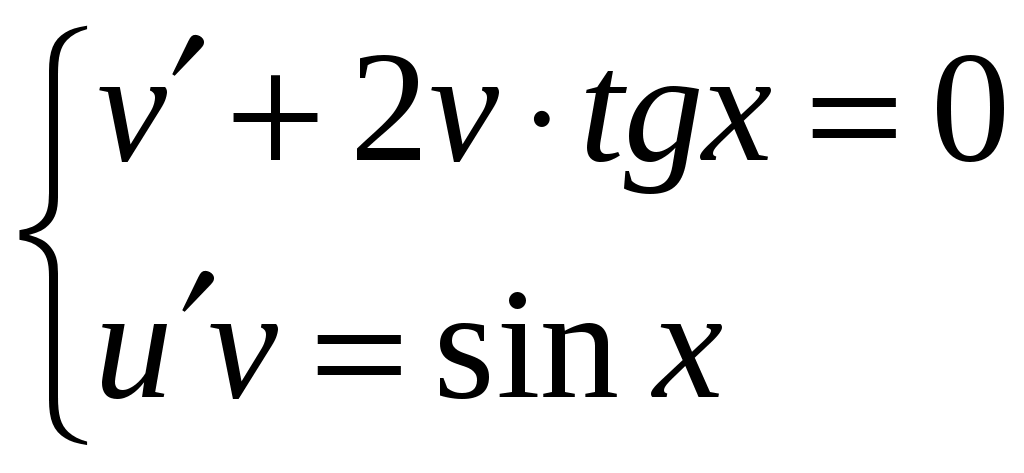
Решим систему.

1)



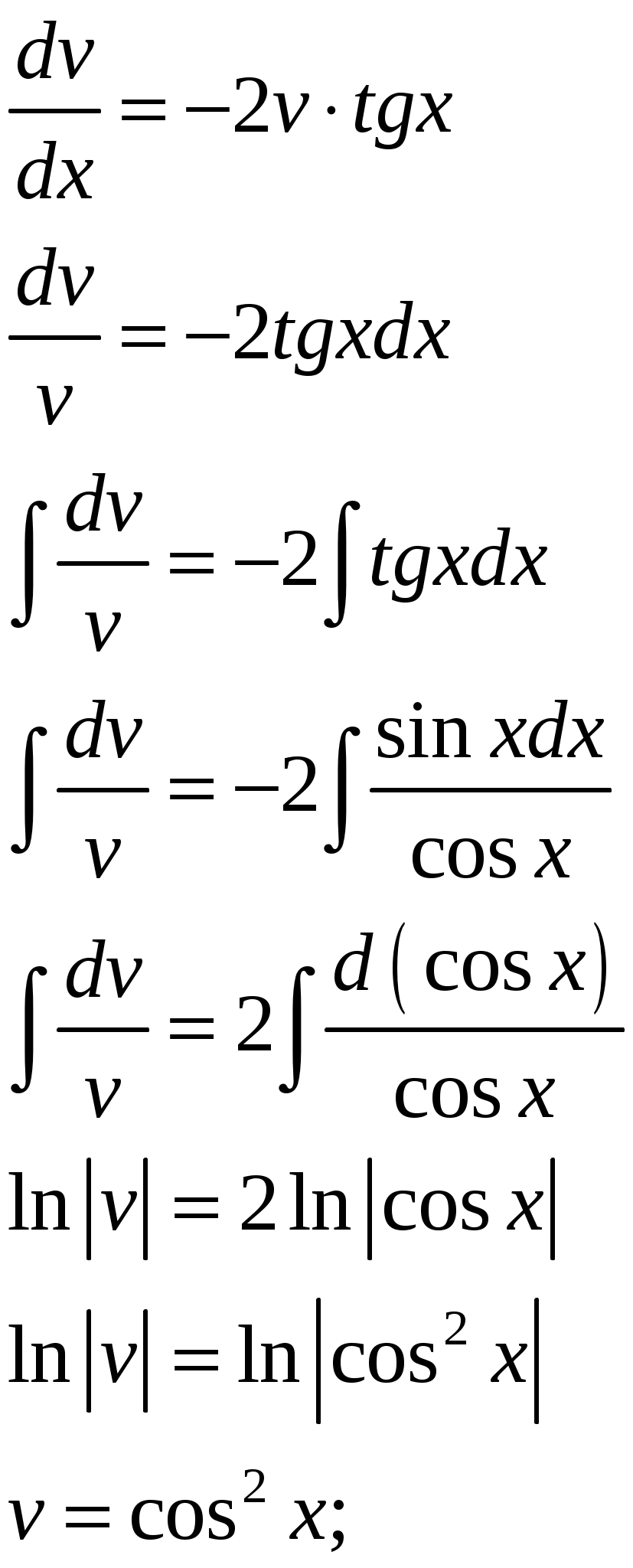
2)



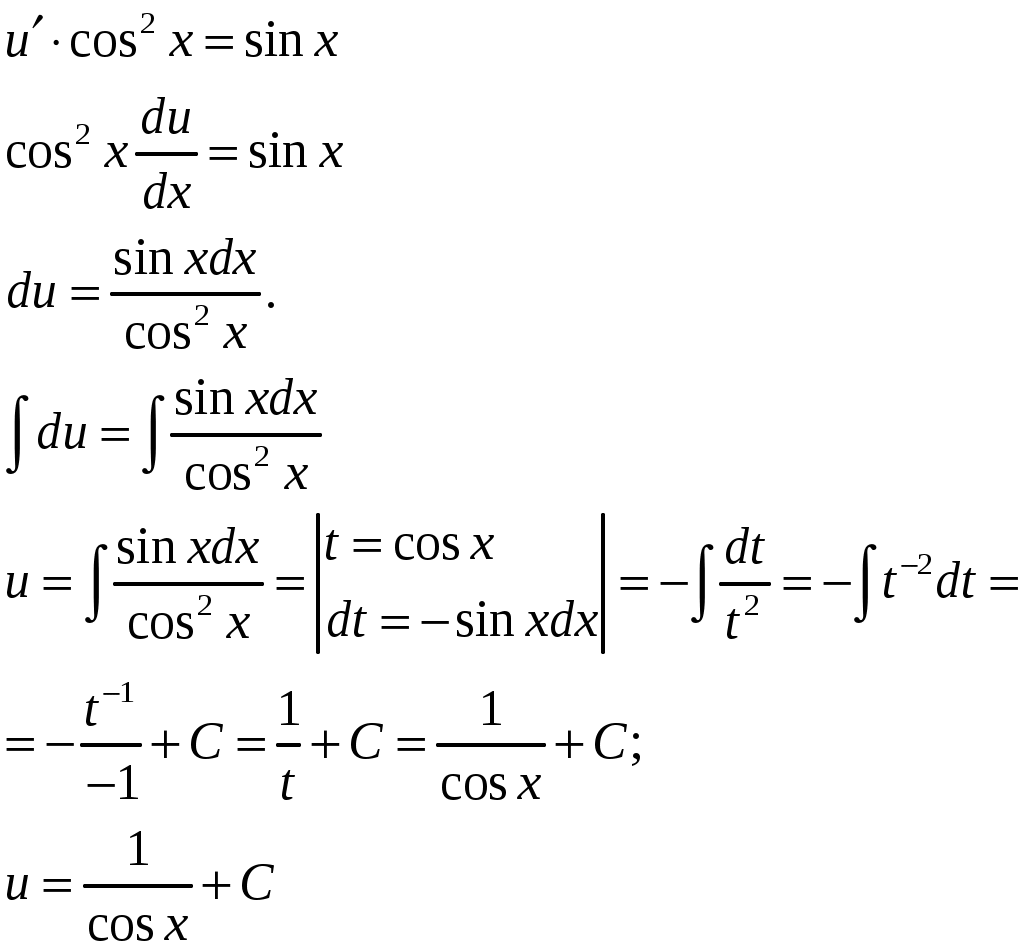
Тогда 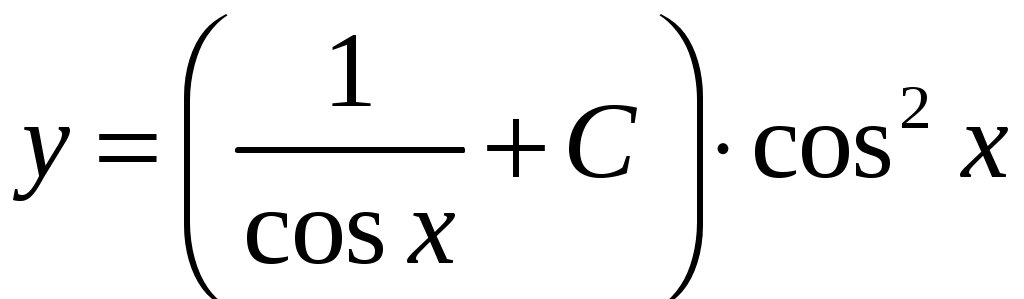, откуда - общее решение.

2) .

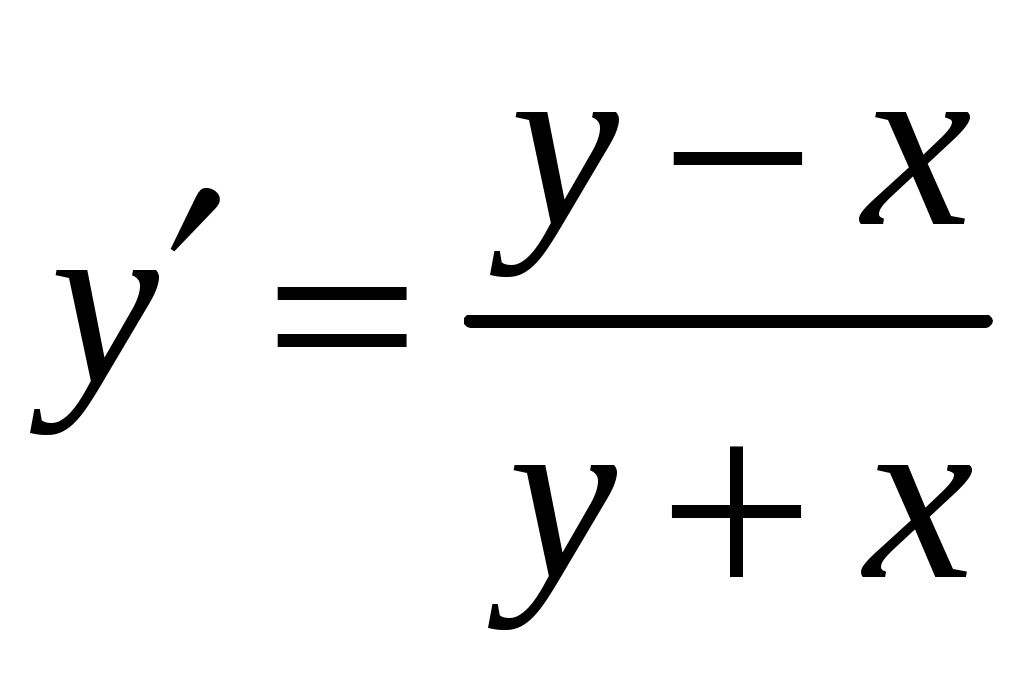Решение.

Приведем уравнение к стандартному виду.



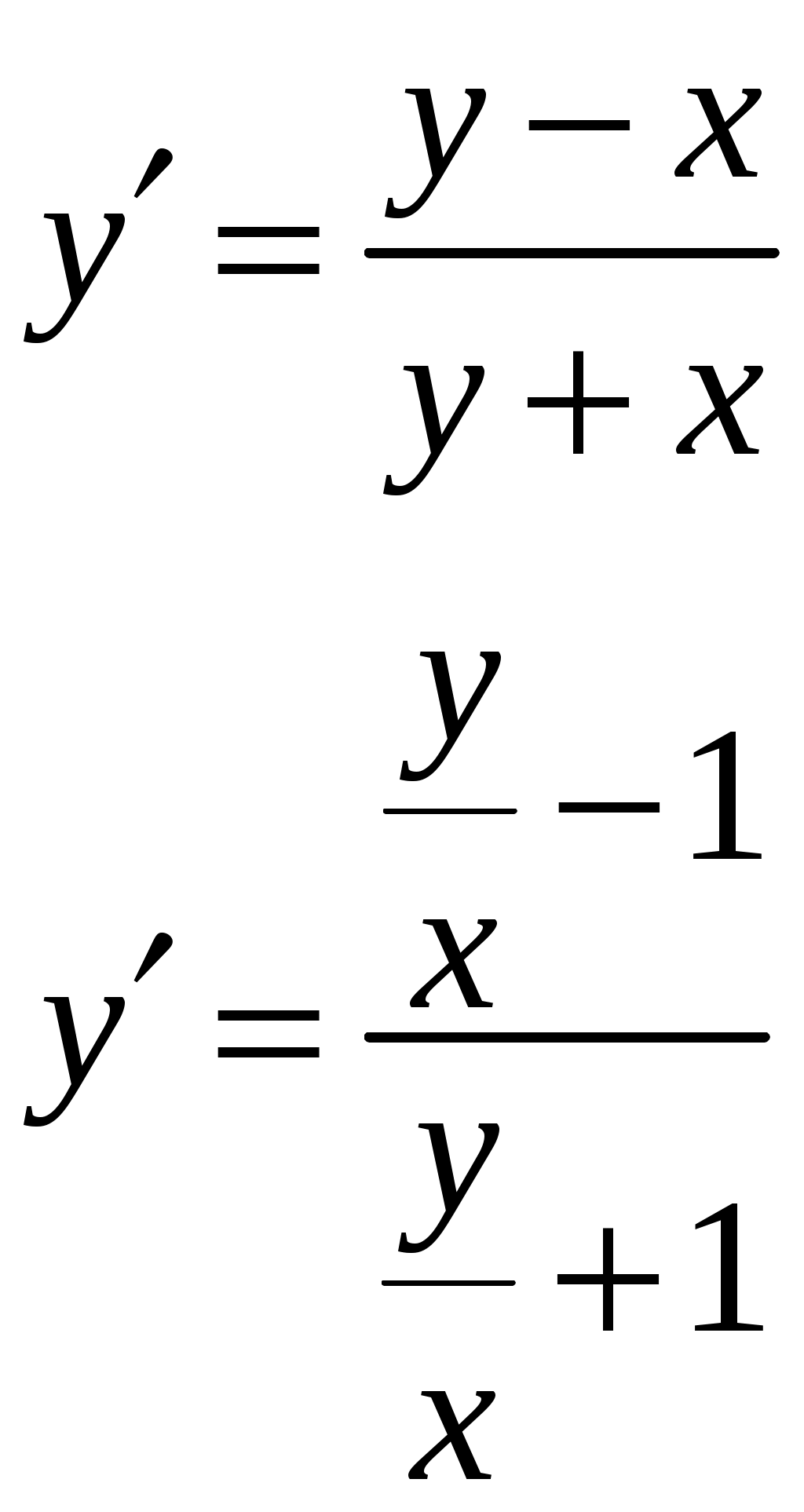
Общий вид уравнения определяется выражением 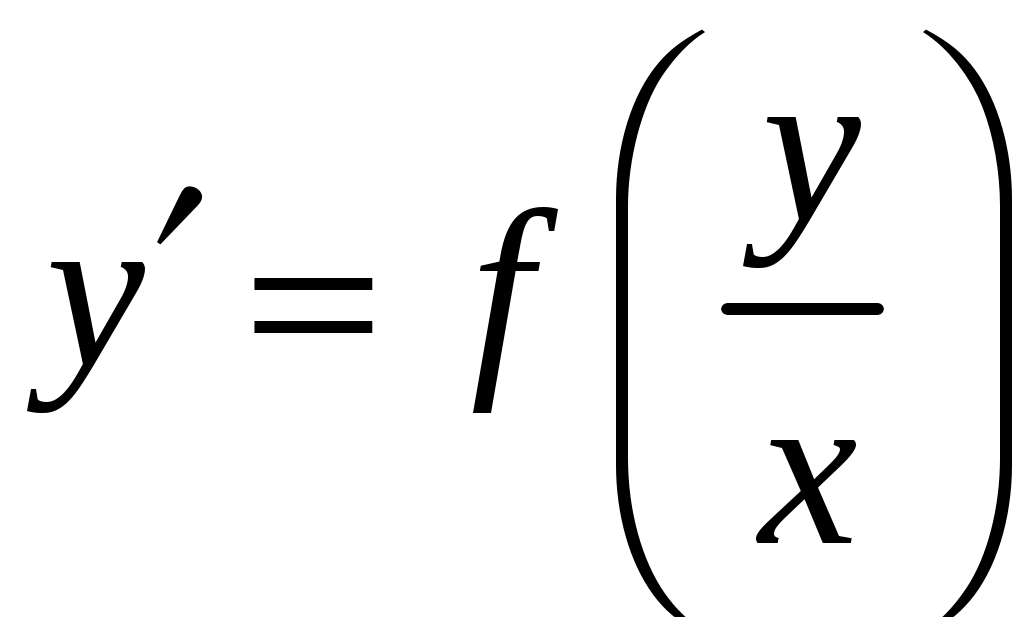‒ это однородное дифференциальное уравнение 1-го порядка.

Пусть 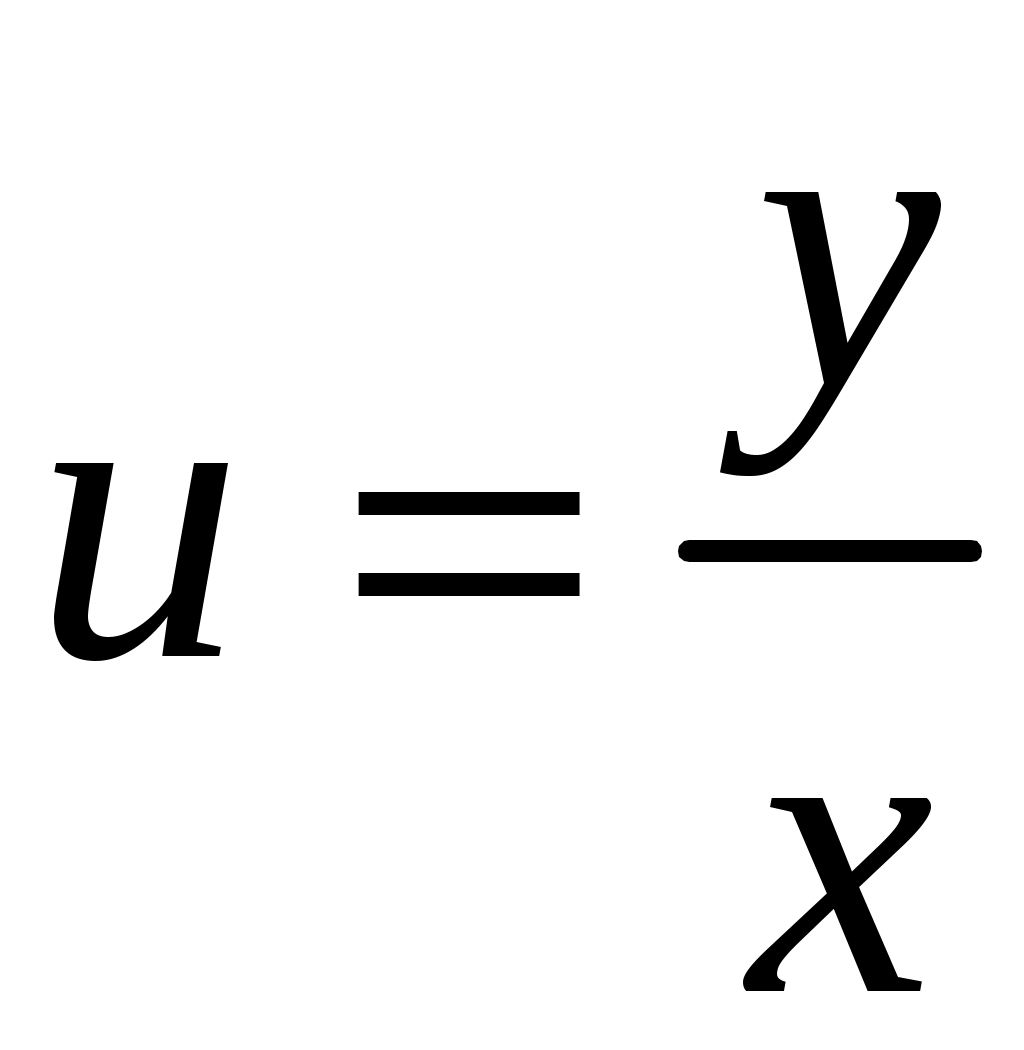, тогда ,

---

.

Подставляя в уравнение, получим:



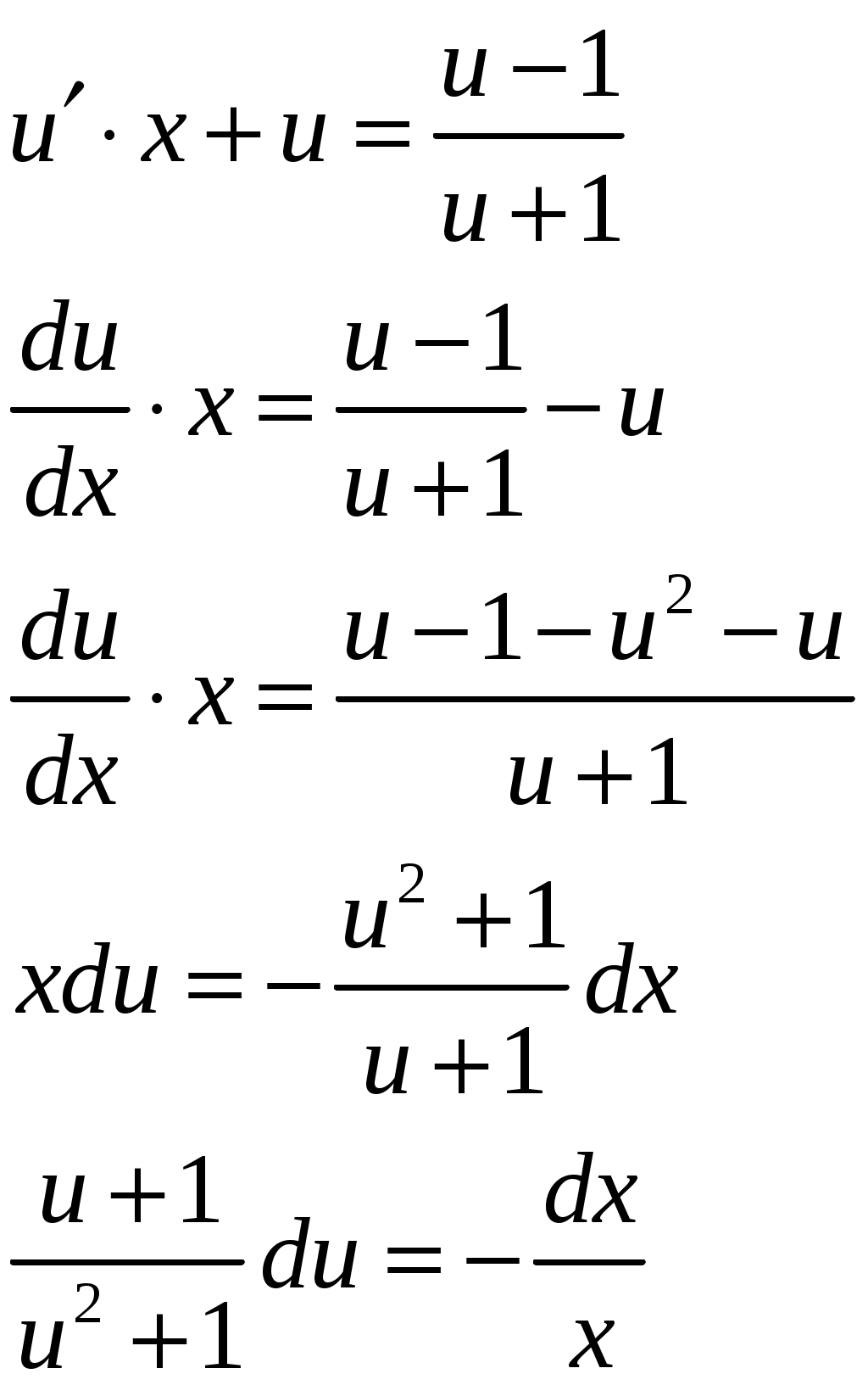
Проинтегрируем обе части:





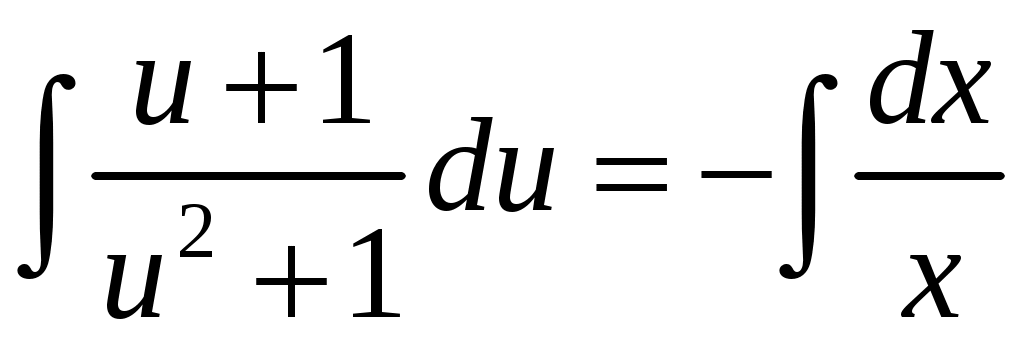
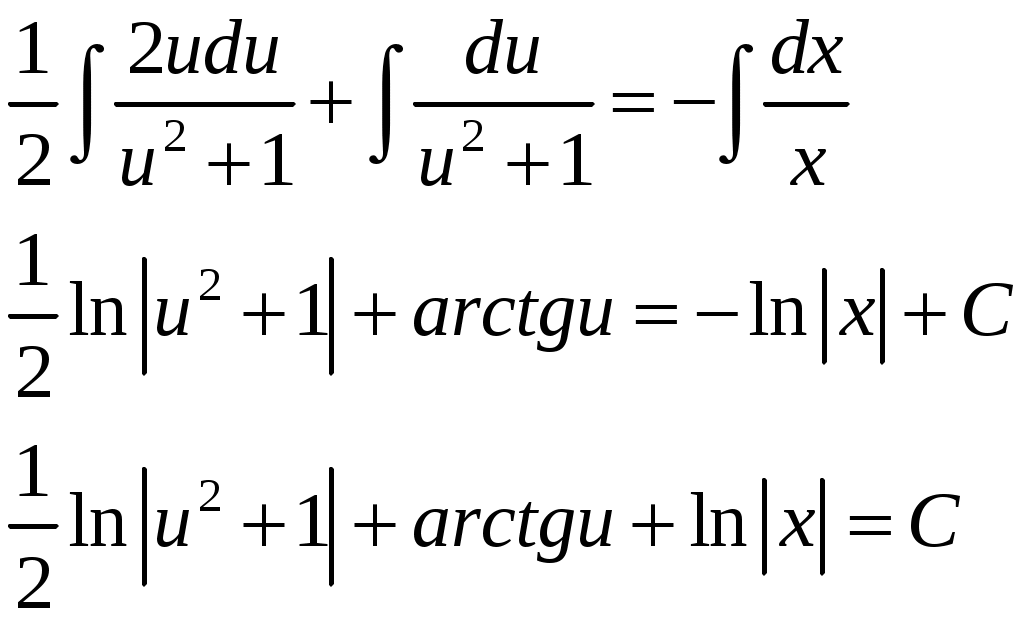
Так как , то получим общий интеграл:

---

Смотрите также файлы

• Основы немедикаментозных методов лечения. Патогенез и саногенез.docx

• Правилами по охране труда при эксплуатации электроустановок (новые Правила 903н от 15. 12. 2020 года старые правила 328н от 24. 07. 2013 года). Было в Правилах 328н.docx

• Задание Составьте.docx

• .docx

• Инструкция по движению поездов и маневровой работе все варианты верны правила выдачи предупреждений на поезда.docx