Файл: Тепломассообмен Методические материалы для студентов Направление подготовки Теплоэнергетика и теплотехника Профиль Энергообеспечение предприятий Составитель доцент кафедры Энергетики и электротехнологии Артамонова Л..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 125
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и поверхностной 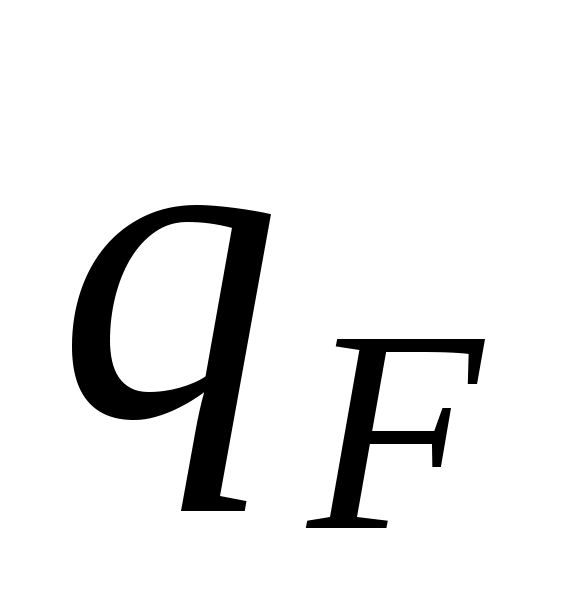 плотностями тепловыделения используется при определении теплового потока на боковых поверхностях пластины
плотностями тепловыделения используется при определении теплового потока на боковых поверхностях пластины
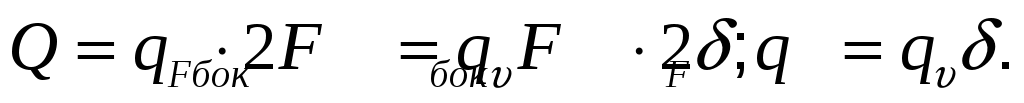
Стационарная теплопроводность цилиндрического стержня с внутренними источниками теплоты.
Для бесконечного стержня (λ=const) задана температура на оси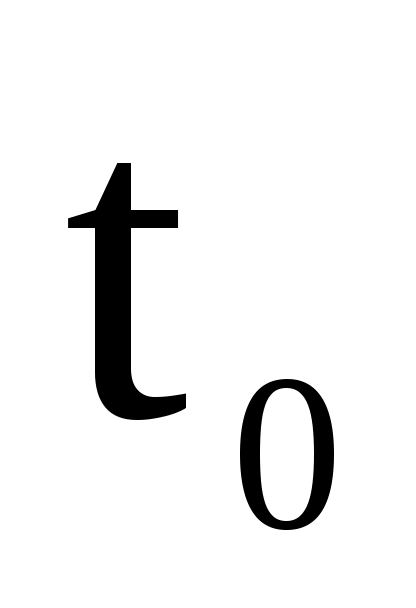
Температурное поле в стержне диаметром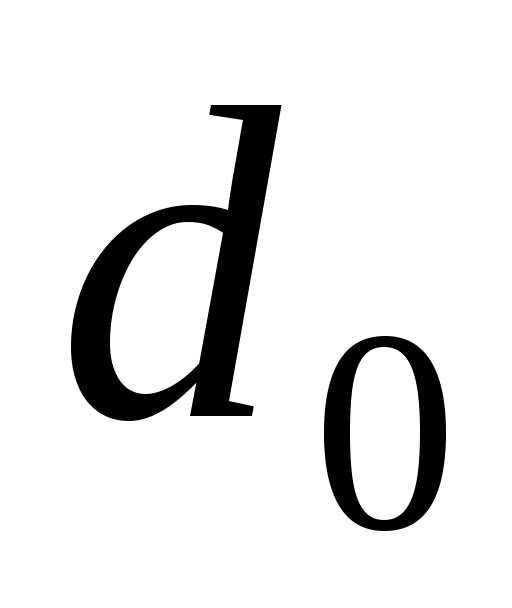
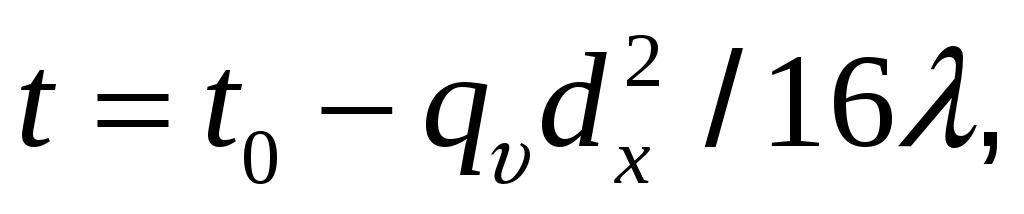
где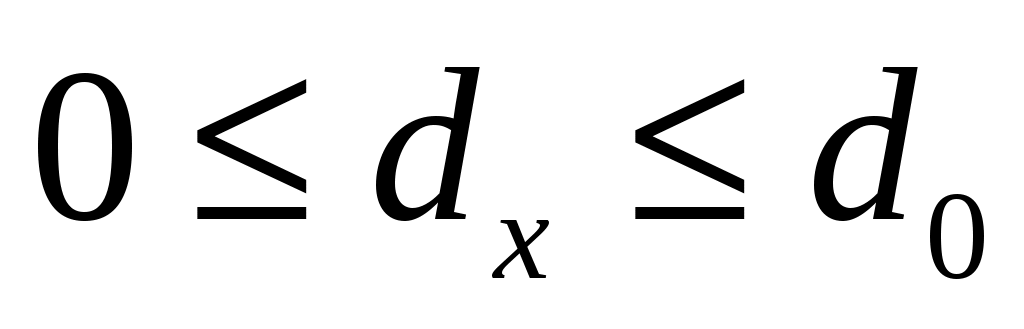 .
.
В формуле при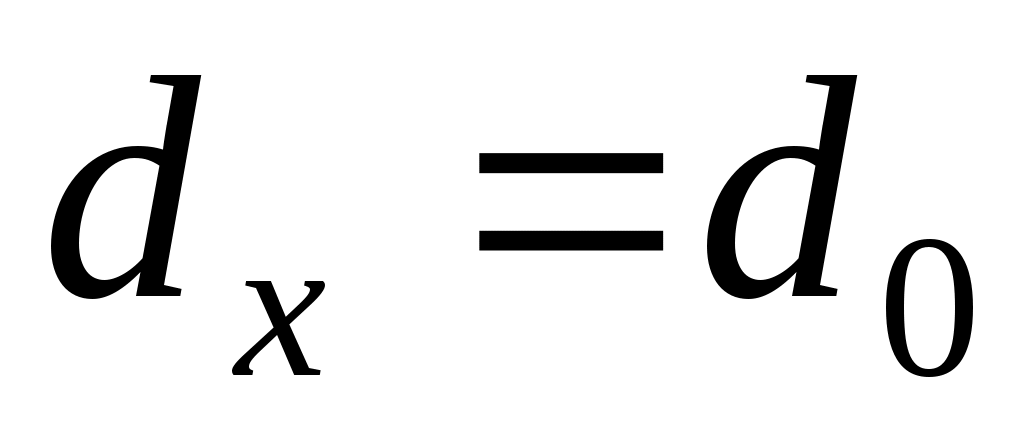 температура на поверхности стержня
температура на поверхности стержня
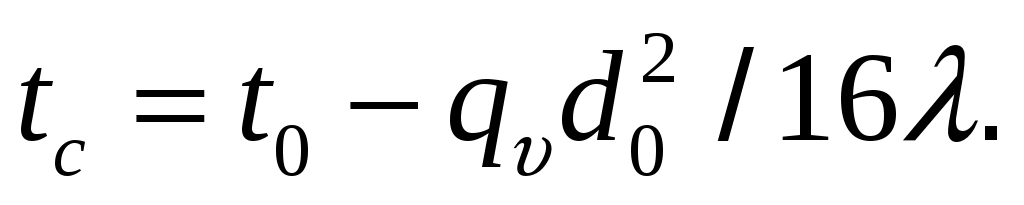
С учетом зависимости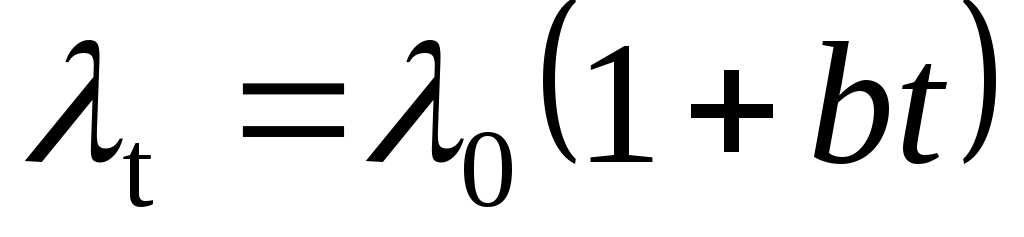 температурное поле в стержне
температурное поле в стержне
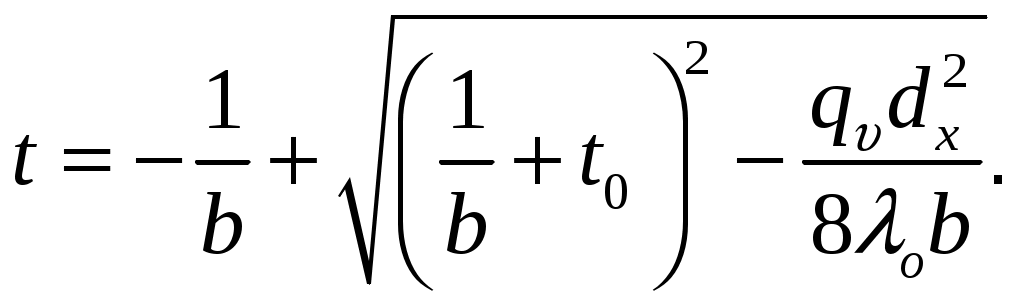
Мощность внутренних источников теплоты для стержня
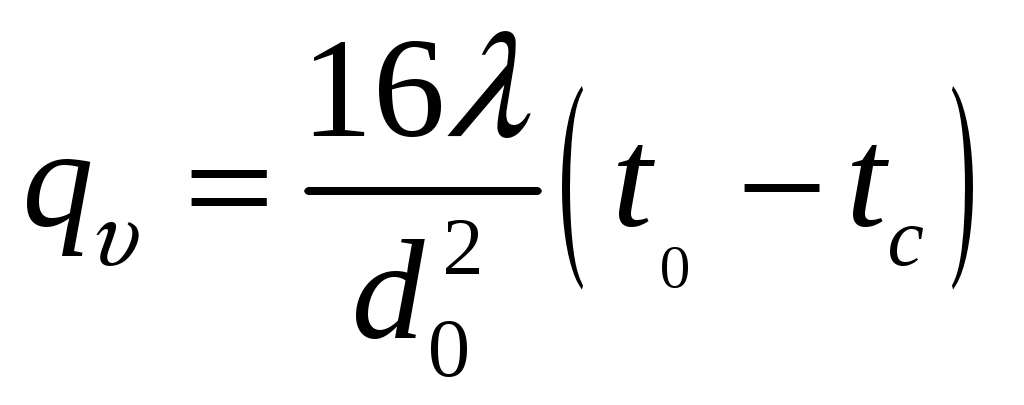 .
.
Стационарная теплопроводность цилиндрической стенки с внутренними источниками теплоты.
Теплота отводится через внешнюю поверхность трубы. Температурное поле в стенке трубы с внутренним радиусом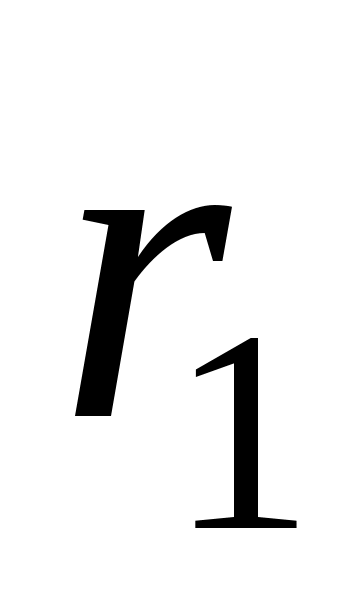 и внешним
и внешним 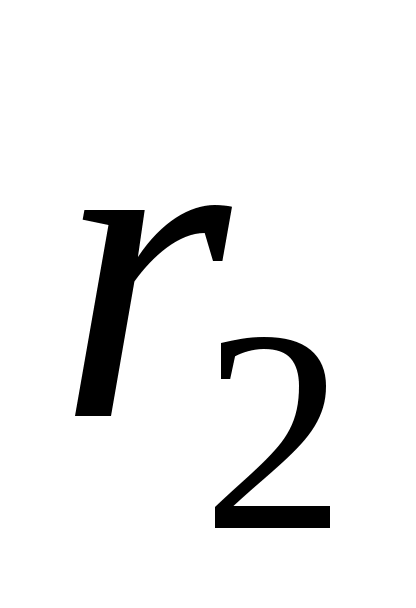
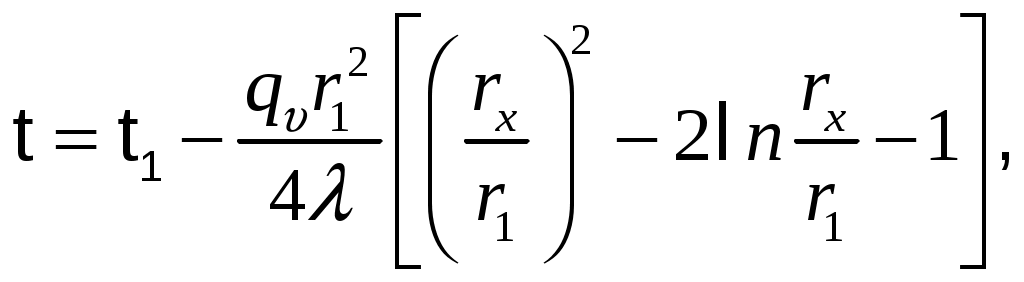
где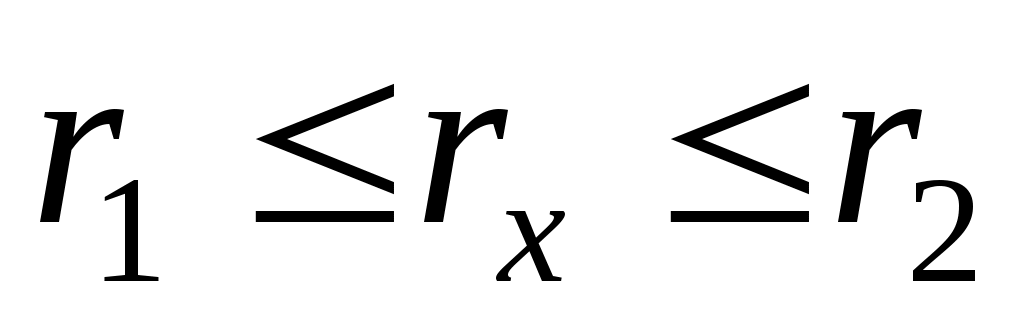 ,
,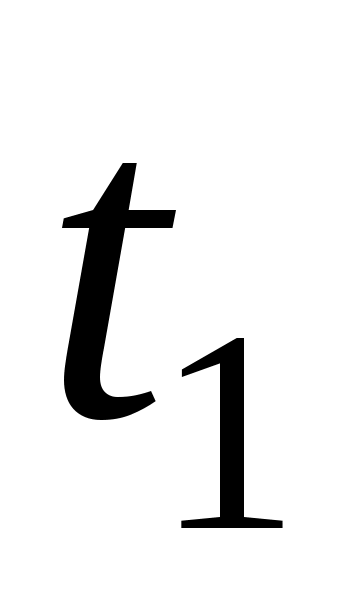 – температура на внутренней теплоизолированной поверхности трубы.
– температура на внутренней теплоизолированной поверхности трубы.
Подставляя в формулу rx=r2, можно получить расчетное выражение для перепада температуры в стенке
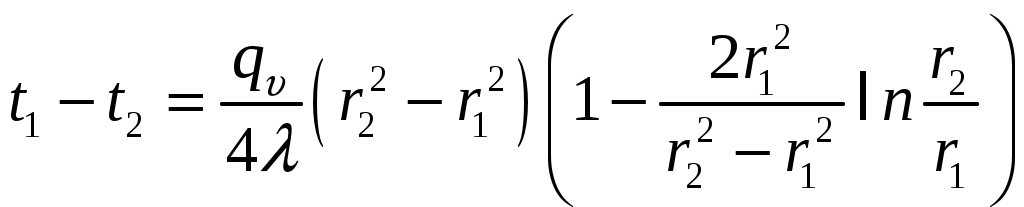
и формулу для линейной плотности теплового потока
где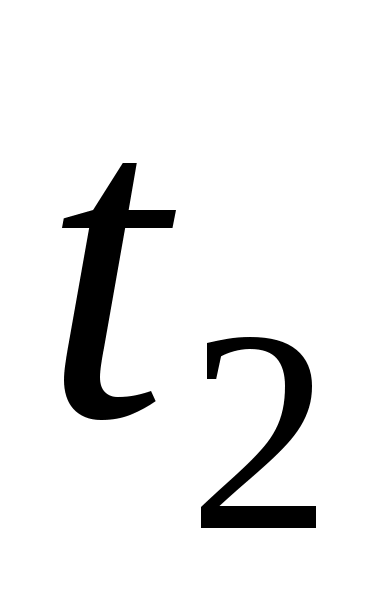 – температура на внешней поверхности трубы.
– температура на внешней поверхности трубы.
Теплота отводится через внутреннююповерхность трубы. Температурное поле в стенке трубы
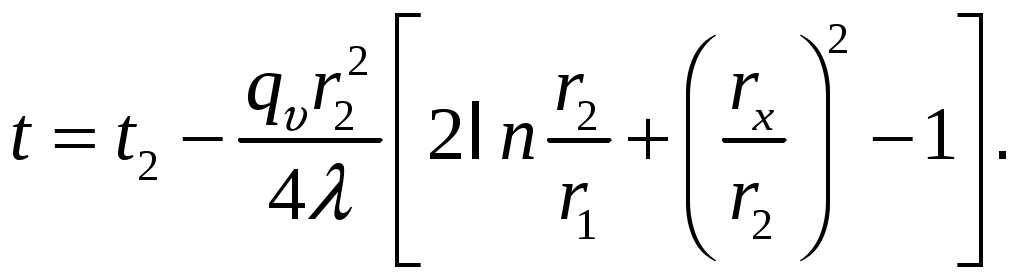
Перепад температур в стенке
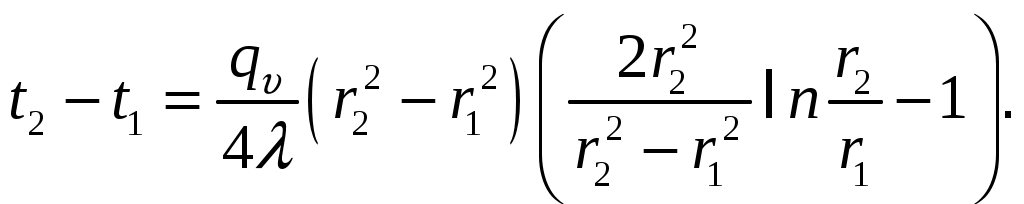
Линейная плотность теплового потока
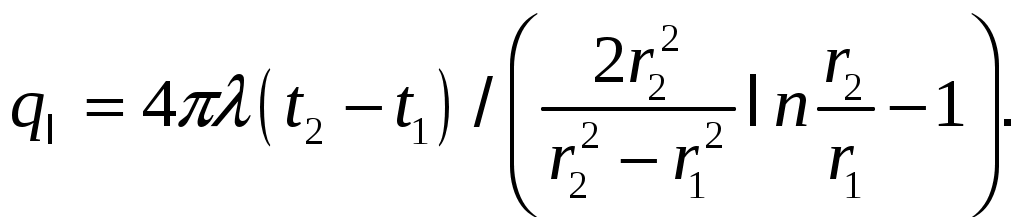
Теплота отводится через обе поверхности трубы. Перепад температур в стенке
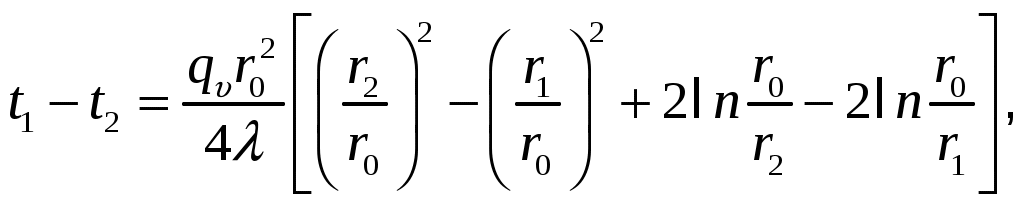
где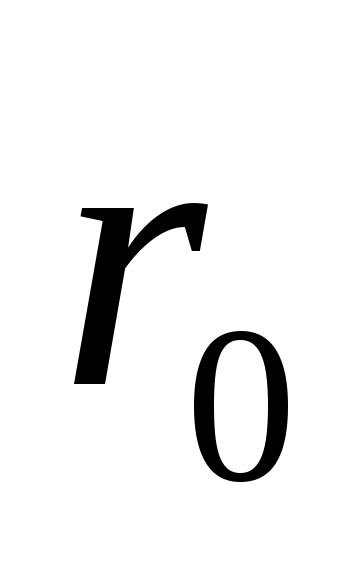 – радиус поверхности, которая имеет наибольшую температуру
– радиус поверхности, которая имеет наибольшую температуру 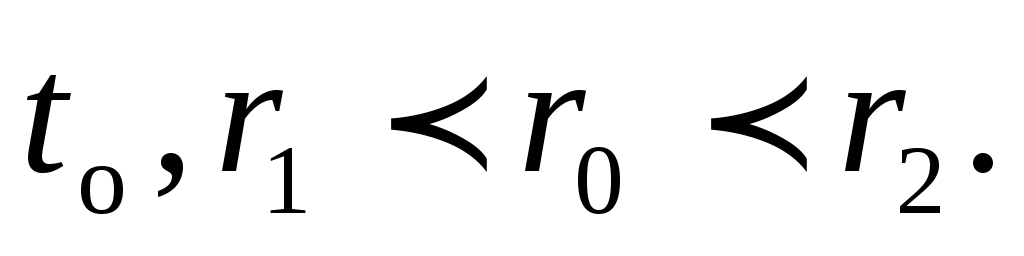
Этот радиус определяется из зависимости
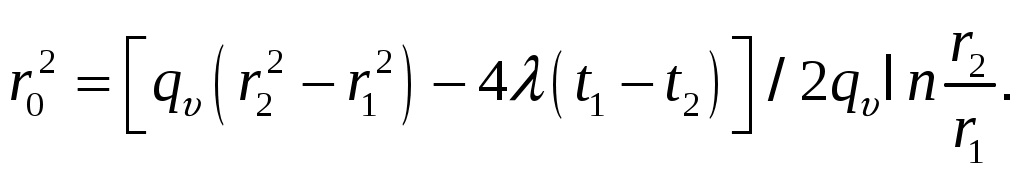
Наибольшую температуру в стенке трубы можно найти по выражению
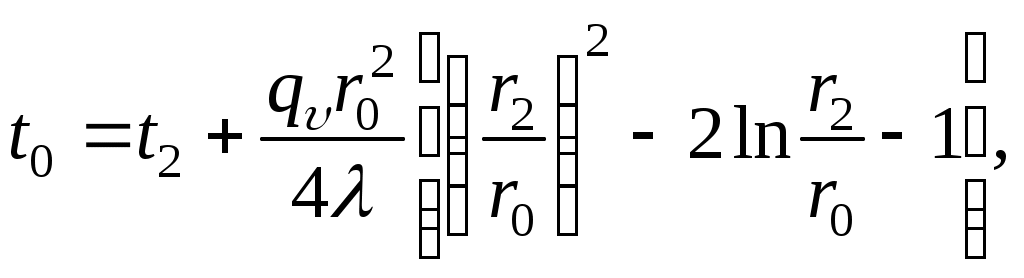
или
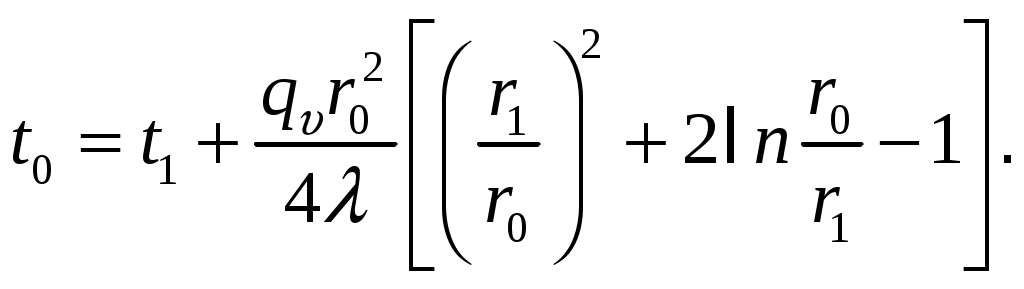
Тема 3. Теплопроводность при нестационарном режиме
Охлаждение (нагрев) пластины, охлаждение (нагрев) бесконечно длинного цилиндра. Охлаждение (нагрев) шара. Определение количества теплоты, отданной (воспринятой) телом в процессе охлаждения (нагрева).
Основные формулы для решения практических задач
Теплопроводность пластины при нестационарном режиме.
Пластина толщиной 2δ. Безразмерная температура пластины
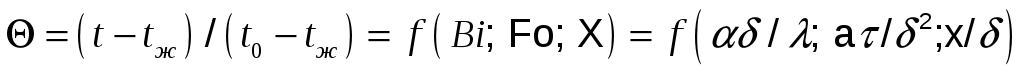
где t –температура в пластине для момента времени т в точке с координатой х; t0 – температура пластины в начальный момент времени.
Если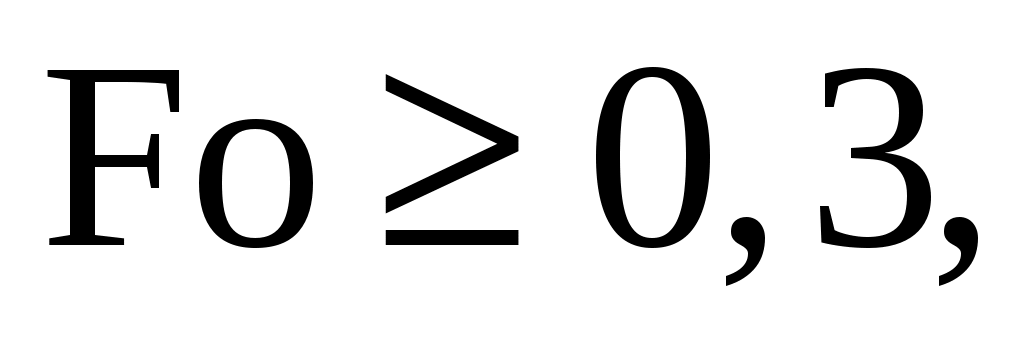
то температура на поверхности пластины (Х=1)
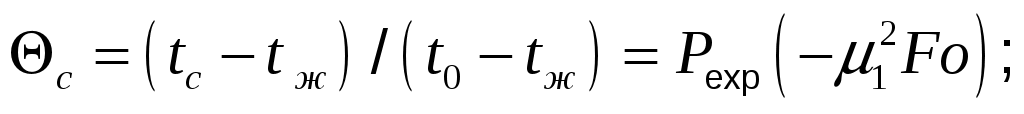
температура на середине толщины пластины (Х=0)
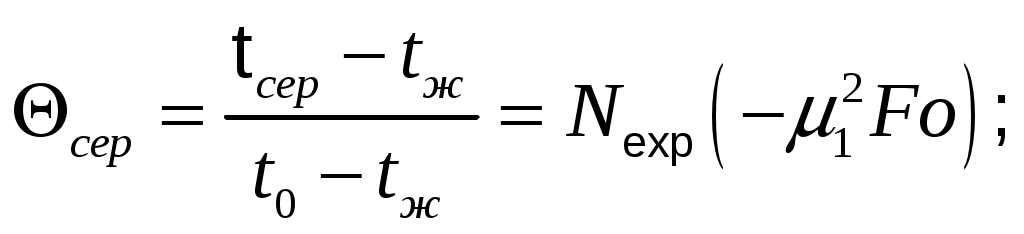
температура внутри пластины на расстоянии х от ее средней плоскости
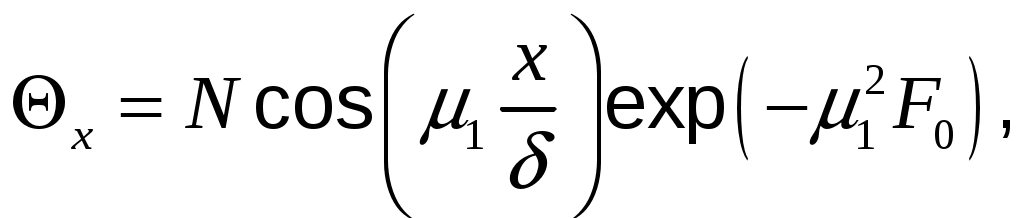
где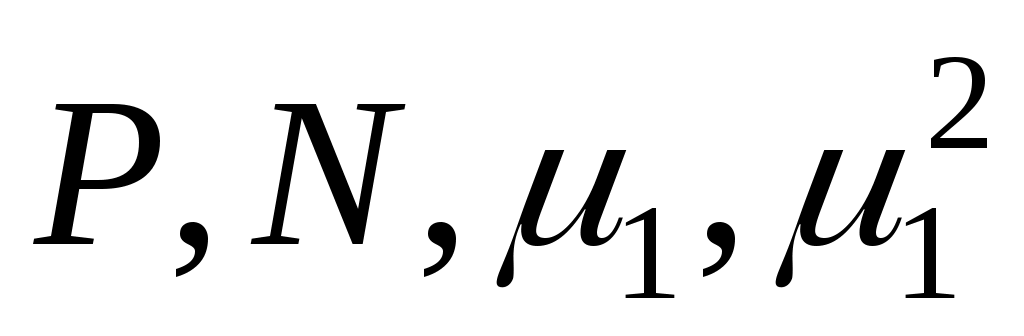 определяются по справочнику для пластины в зависимости от числа Bi.
определяются по справочнику для пластины в зависимости от числа Bi.
Температура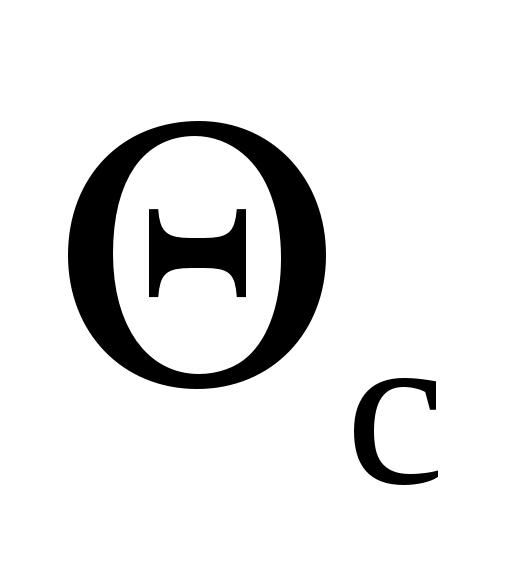 и
и  можно определить по графикам по известным числам Bi и Fo.
можно определить по графикам по известным числам Bi и Fo.
Теплопроводность цилиндра при нестационарном режиме.
Цилиндр радиусом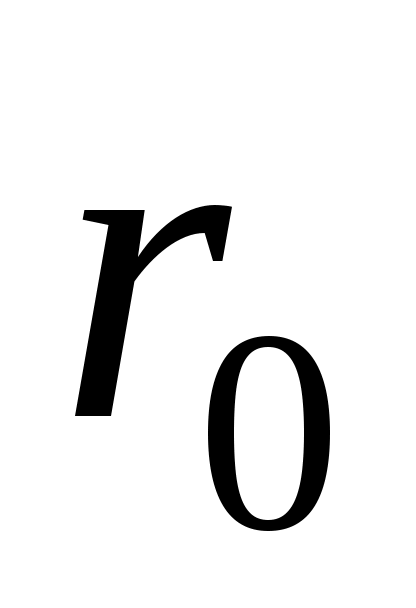 .Безразмерная температура цилиндра
.Безразмерная температура цилиндра
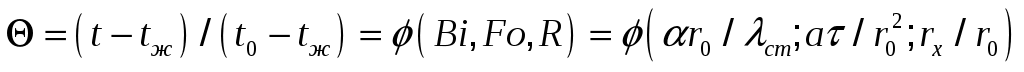 ,
,
где t – искомая температура в цилиндре для радиуса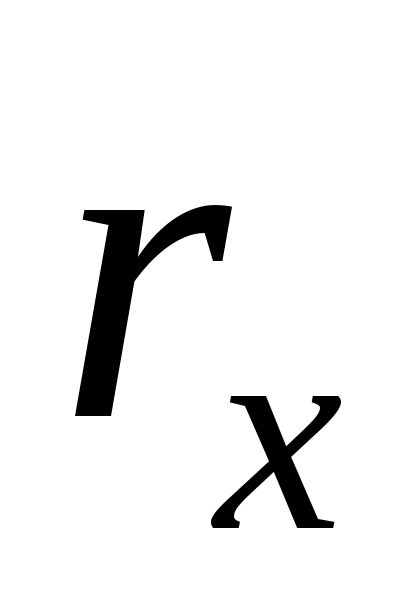 и времени
и времени  ,
, 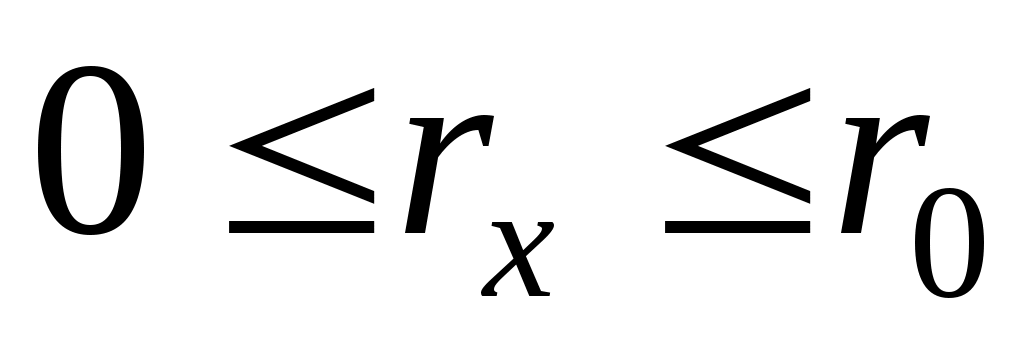 .
.
Если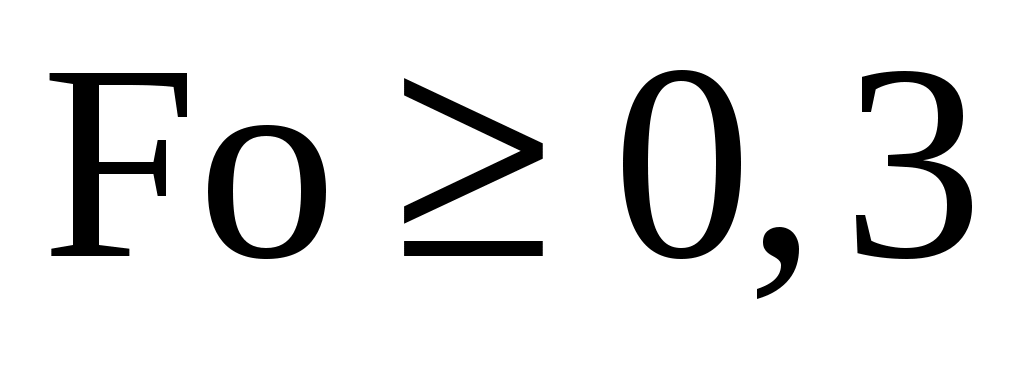 , то температура на поверхности цилиндра
, то температура на поверхности цилиндра 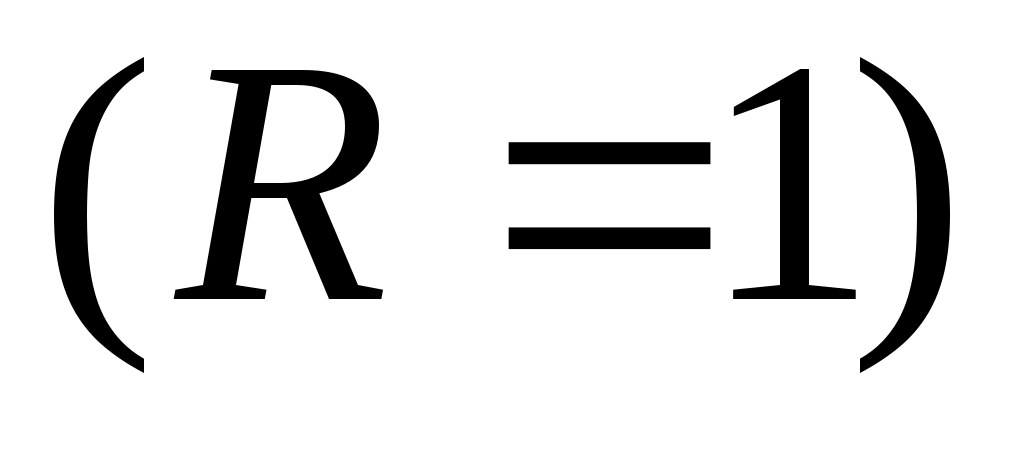
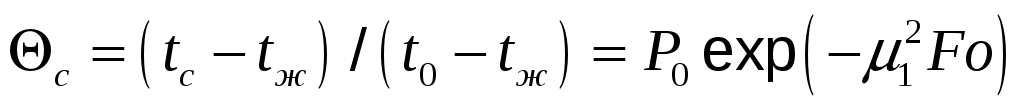
температура на оси цилиндра (R=0)
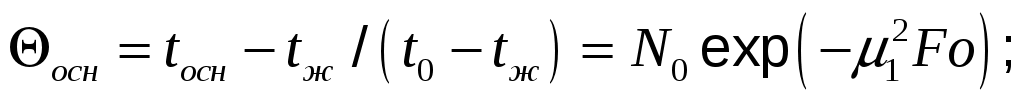
температура внутри цилиндра для радиуса rх
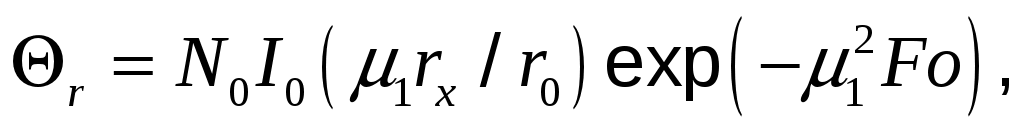
где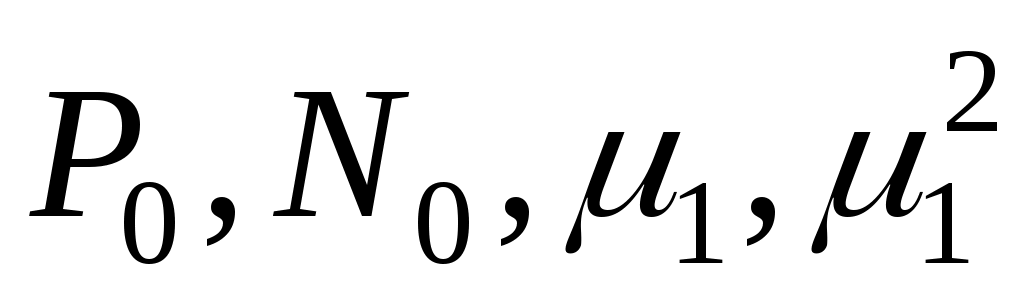 – определяются по справочнику для цилиндра в зависимости от числа Bi; I0(μ1rx/r0) – функция Бесселя первого рода нулевого порядка.
– определяются по справочнику для цилиндра в зависимости от числа Bi; I0(μ1rx/r0) – функция Бесселя первого рода нулевого порядка.
Температуры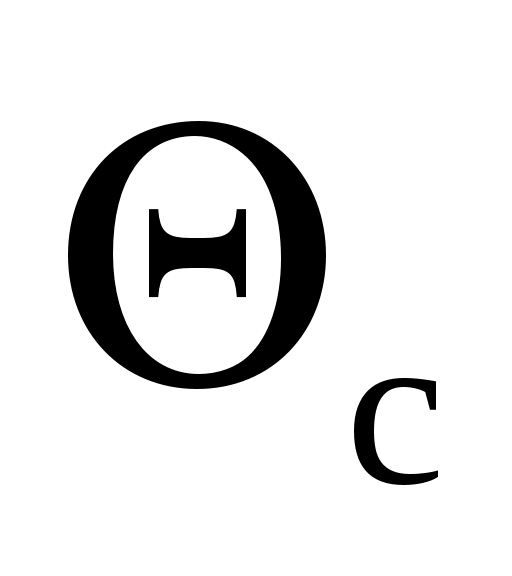 и
и 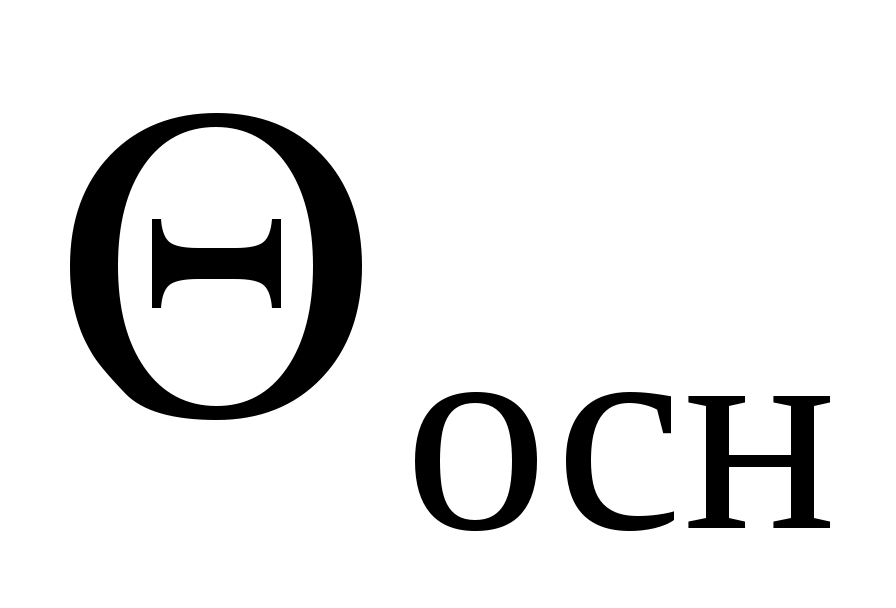
и можно определить по графикам по известным числам Bi и Fo.
Количество теплоты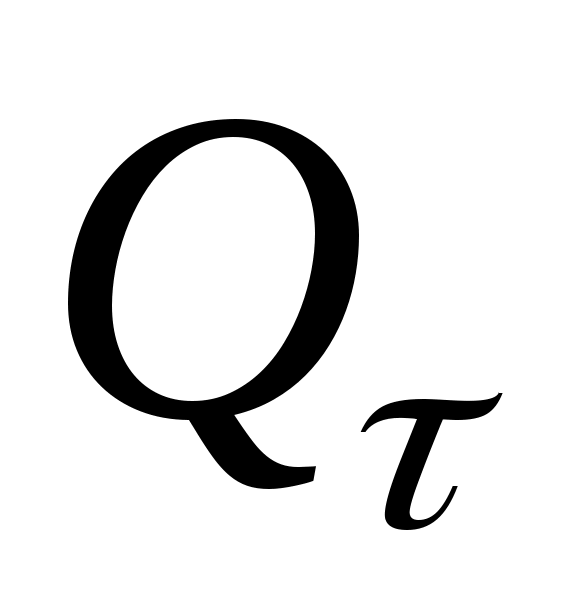 , Дж, отданной (воспринятой) телом за время τ в процессе охлаждения (нагревания), равно
, Дж, отданной (воспринятой) телом за время τ в процессе охлаждения (нагревания), равно
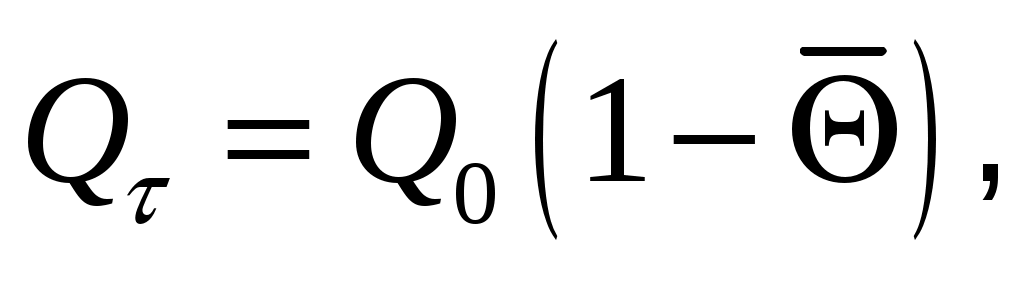
где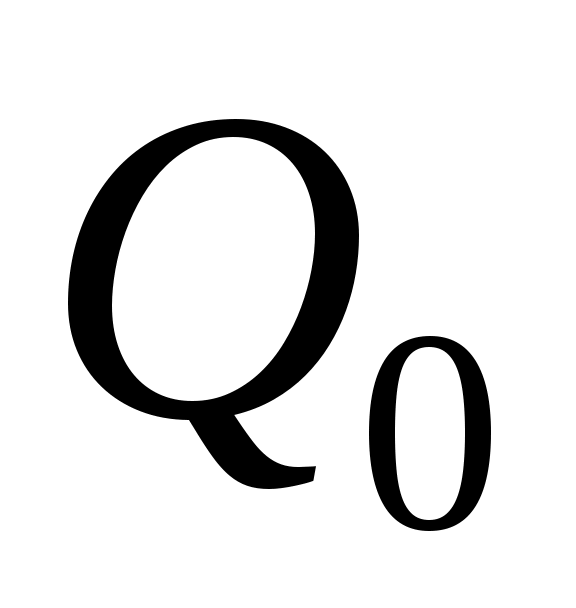 – количество теплоты, переданной за время полного охлаждения (нагревания), Дж;
– количество теплоты, переданной за время полного охлаждения (нагревания), Дж;  – средняя по объему безразмерная температура тела в момент времени
– средняя по объему безразмерная температура тела в момент времени  .
.
Для пластинытолщиной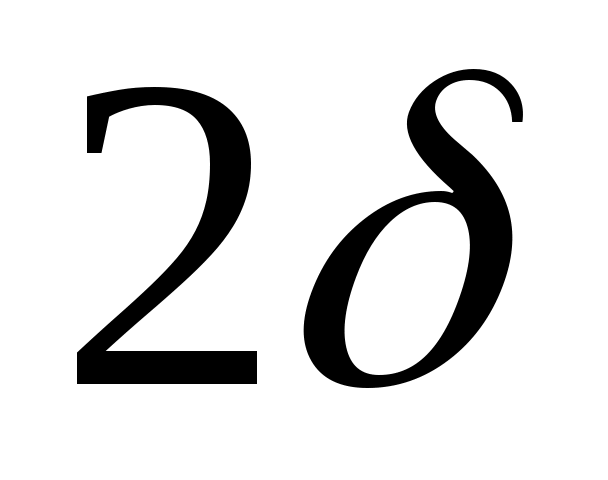 и площадью поверхности Fтеплота, переданная за время полного охлаждения, равна
и площадью поверхности Fтеплота, переданная за время полного охлаждения, равна
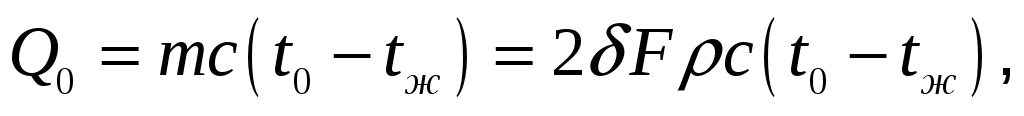
где m – масса пластины, кг; с – теплоемкость материала пластины, Дж/(кг·К);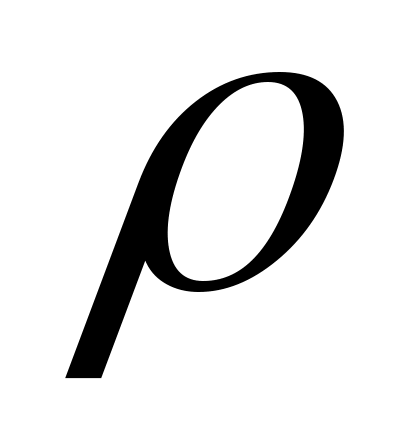 – его плотность, кг/м3.
– его плотность, кг/м3.
Средняя по объему безразмерная температура пластины в момент времени τ при
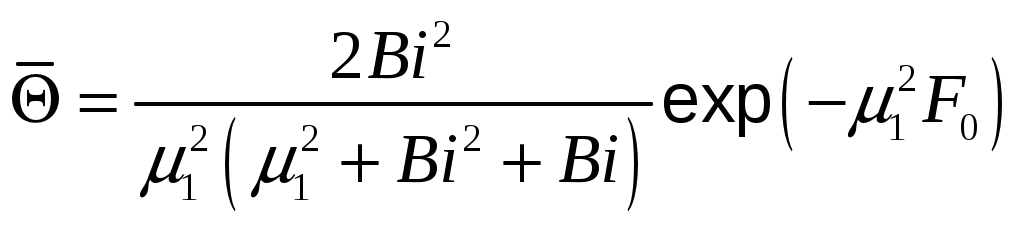 \
\
Для цилиндрарадиусом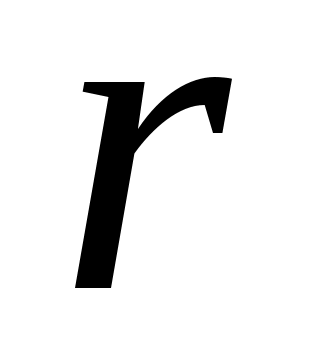 0 и длиной
0 и длиной  теплота, отданная за время полного охлаждения, равна
теплота, отданная за время полного охлаждения, равна
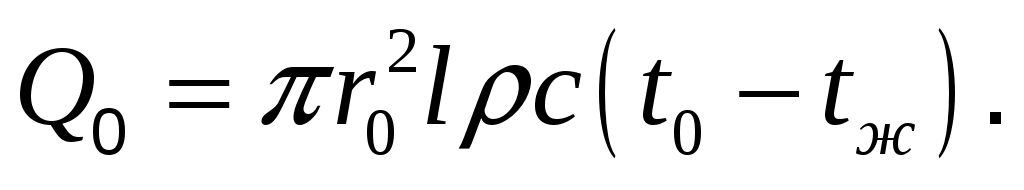
Средняя по объему безразмерная температура цилиндра в момент времени при
при 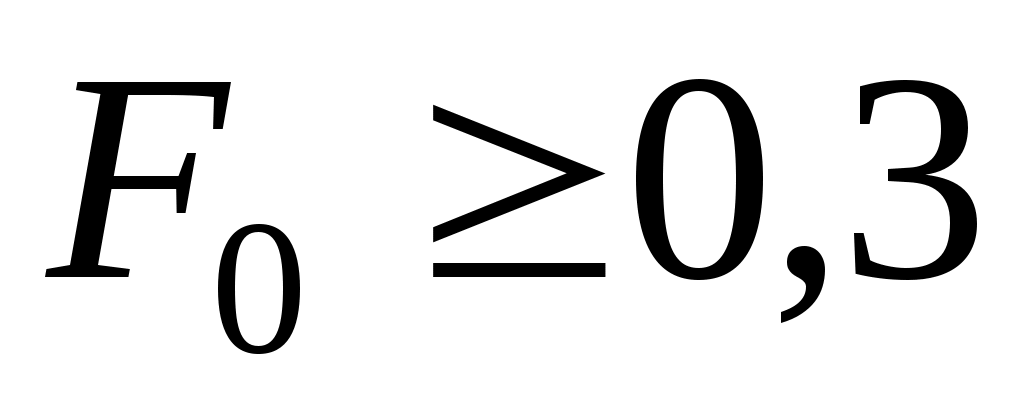 равна
равна
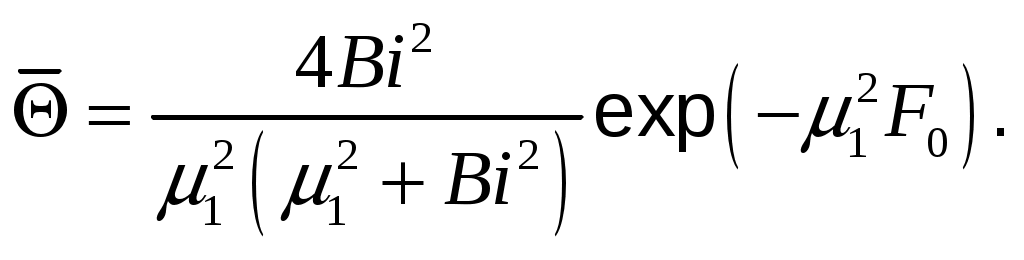
Тема 4. Конвективный теплообмен
Физическая сущность конвективного теплообмена. Формула Ньютона — Рихмана. Коэффициент теплоотдачи. Основы теории подобия. Критерии подобия и принцип их получения. Критериальное уравнение конвективного теплообмена. Определяющие и определяемые критерии подобия. Определяющая температура и определяющий линейный размер. Теплообмен при вынужденном движении жидкости или газа в трубах и каналах. Теплообмен при вынужденном поперечном омывании труб. Теплообмен при свободном движении жидкости. Теплообмен при изменении агрегатного состояния вещества.
Основные формулы для решения практических задач
Расчетные формулы для теплоотдачи при продольном обтекании пластины
При движении потока вдоль плоской поверхности, имеющей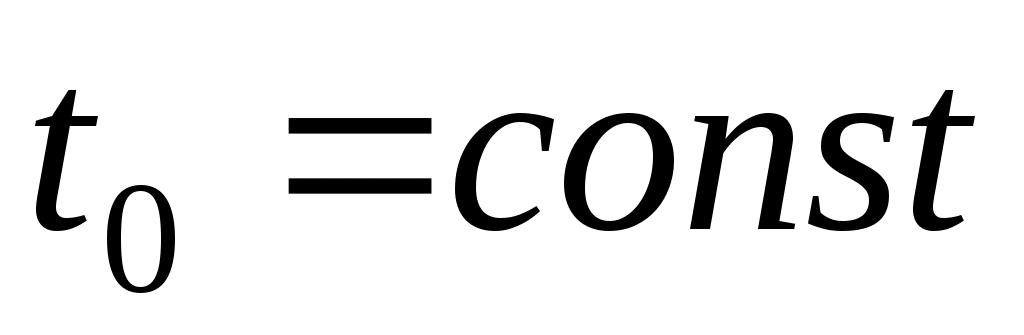 , и ламинарном режиме
, и ламинарном режиме 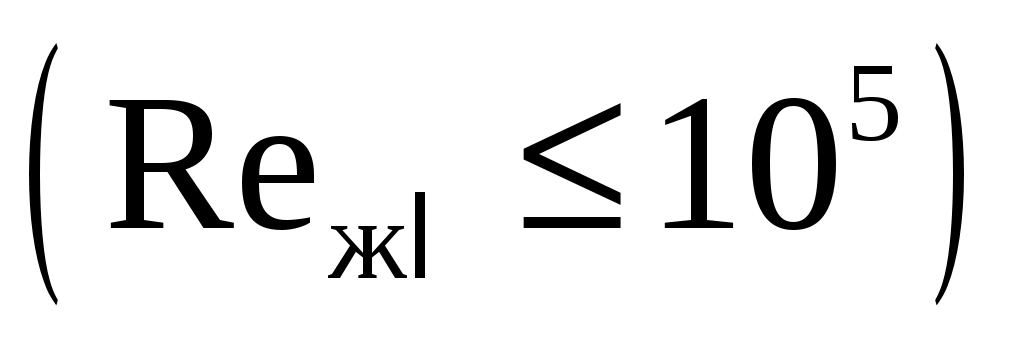 среднее значение числа Нуссельта:
среднее значение числа Нуссельта:
для капельной жидкости
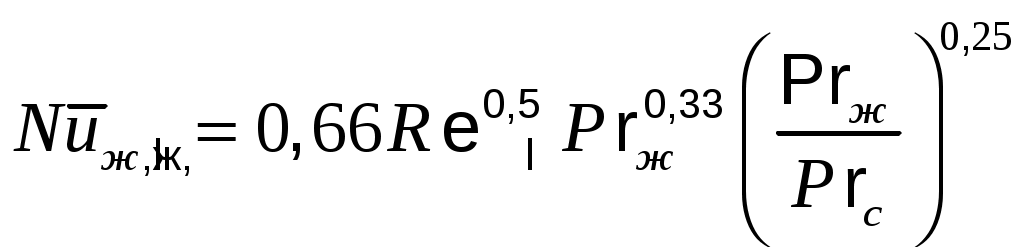
для воздуха
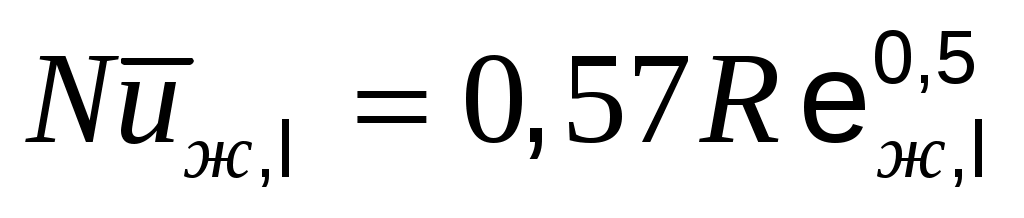
При турбулентномрежиме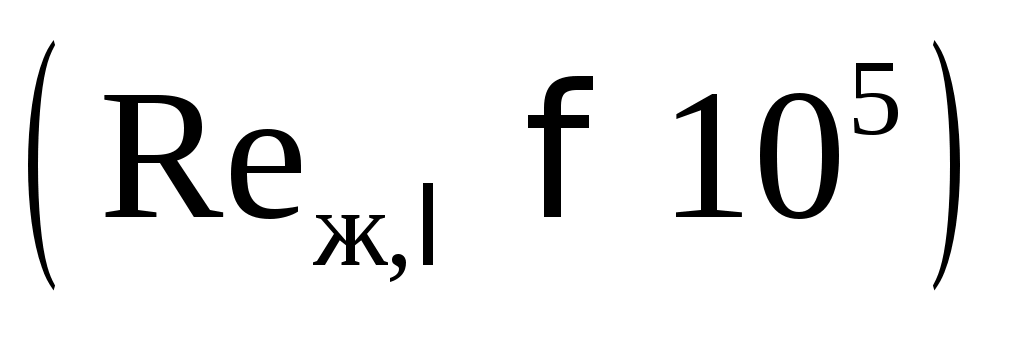 :
:
для капельной жидкости
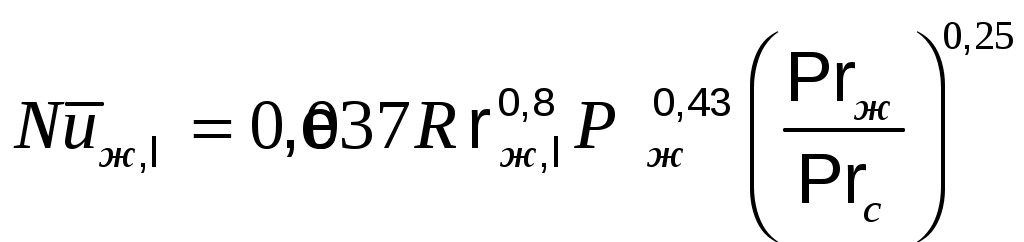
для воздуха
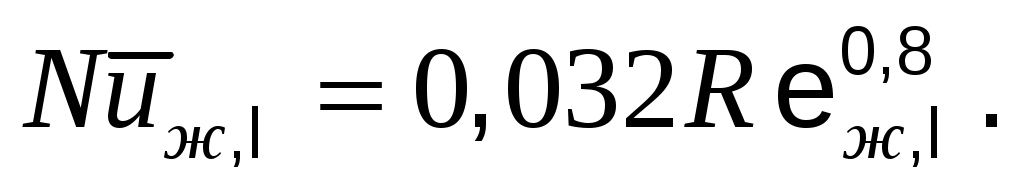
Определяющей принимается температура набегающего потока (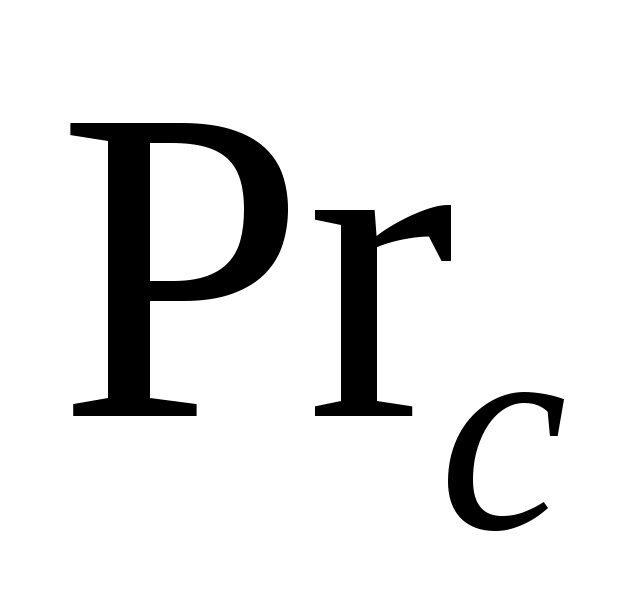 определяется по
определяется по 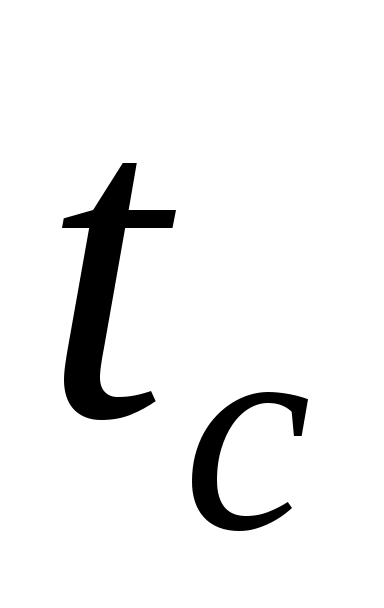 ), определяющим геометрическим размером – длина
), определяющим геометрическим размером – длина  стенки по направлению потока.
стенки по направлению потока.
Местный коэффициент теплоотдачи на расстоянии х от передней кромки пластины определяется по формулам:
при ламинарном режиме течения в пограничном слое
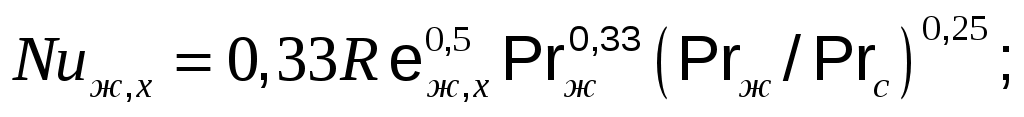
Стационарная теплопроводность цилиндрического стержня с внутренними источниками теплоты.
Для бесконечного стержня (λ=const) задана температура на оси
Температурное поле в стержне диаметром
где
В формуле при
С учетом зависимости
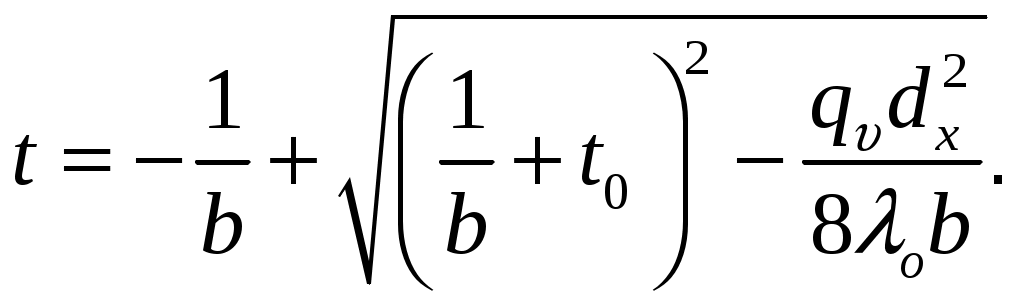
Мощность внутренних источников теплоты для стержня
Стационарная теплопроводность цилиндрической стенки с внутренними источниками теплоты.
Теплота отводится через внешнюю поверхность трубы. Температурное поле в стенке трубы с внутренним радиусом
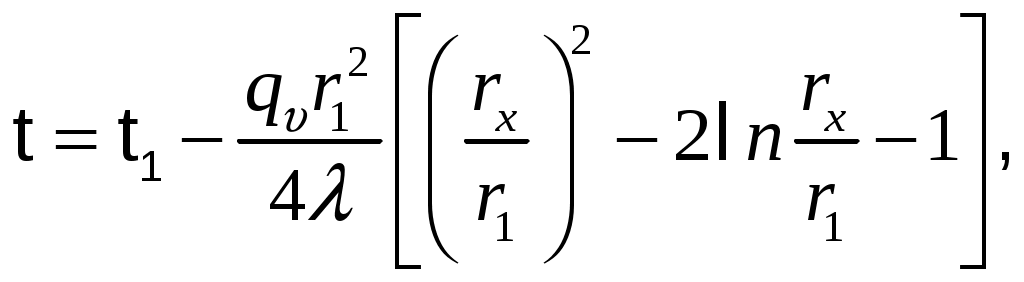
где
Подставляя в формулу rx=r2, можно получить расчетное выражение для перепада температуры в стенке
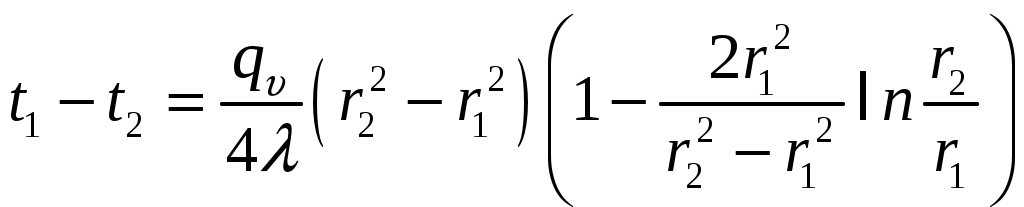
и формулу для линейной плотности теплового потока
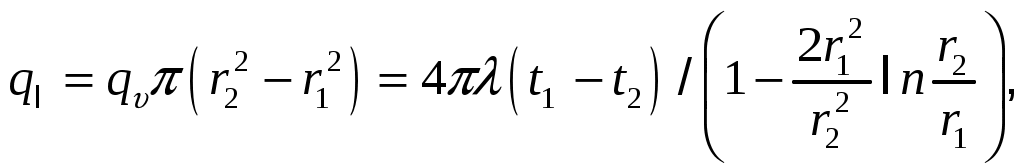
где
Теплота отводится через внутреннююповерхность трубы. Температурное поле в стенке трубы
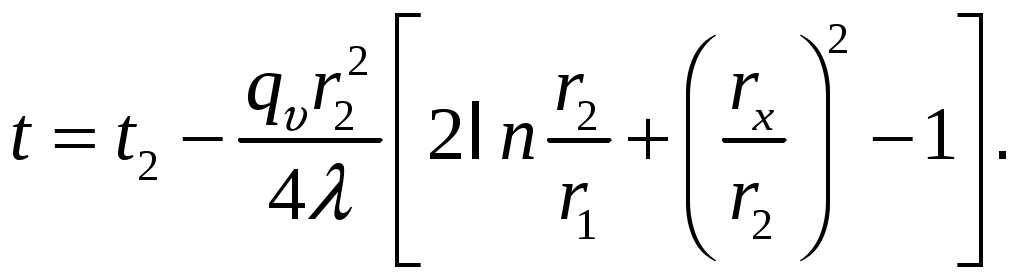
Перепад температур в стенке
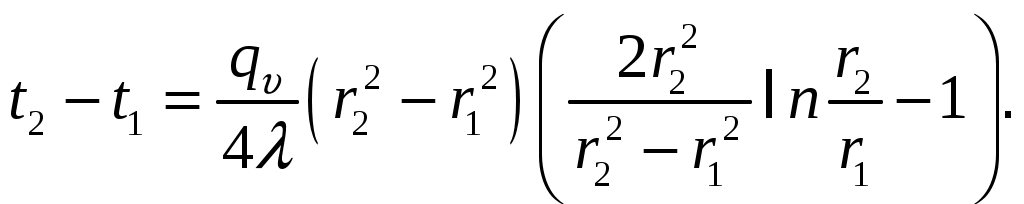
Линейная плотность теплового потока
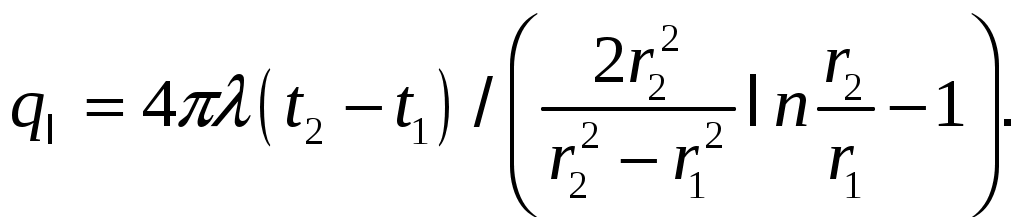
Теплота отводится через обе поверхности трубы. Перепад температур в стенке
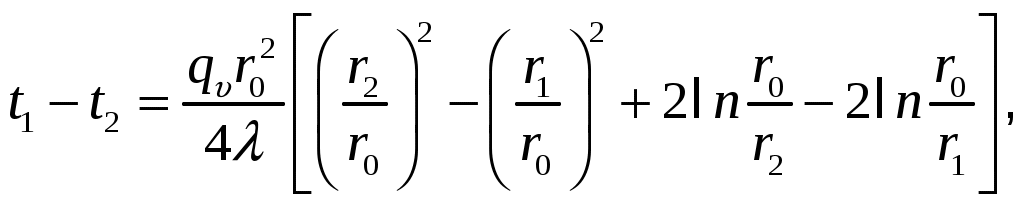
где
Этот радиус определяется из зависимости
Наибольшую температуру в стенке трубы можно найти по выражению
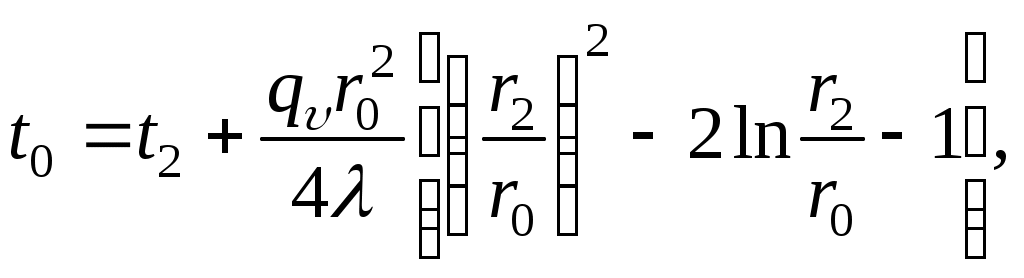
или
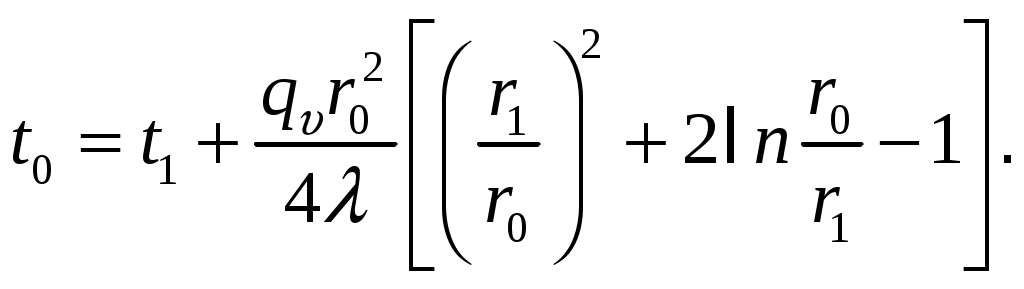
Тема 3. Теплопроводность при нестационарном режиме
Охлаждение (нагрев) пластины, охлаждение (нагрев) бесконечно длинного цилиндра. Охлаждение (нагрев) шара. Определение количества теплоты, отданной (воспринятой) телом в процессе охлаждения (нагрева).
Основные формулы для решения практических задач
Теплопроводность пластины при нестационарном режиме.
Пластина толщиной 2δ. Безразмерная температура пластины
где t –температура в пластине для момента времени т в точке с координатой х; t0 – температура пластины в начальный момент времени.
Если
то температура на поверхности пластины (Х=1)
температура на середине толщины пластины (Х=0)
температура внутри пластины на расстоянии х от ее средней плоскости
где
Температура
Теплопроводность цилиндра при нестационарном режиме.
Цилиндр радиусом
где t – искомая температура в цилиндре для радиуса
Если
температура на оси цилиндра (R=0)
температура внутри цилиндра для радиуса rх
где
Температуры
и можно определить по графикам по известным числам Bi и Fo.
Количество теплоты
где
Для пластинытолщиной
где m – масса пластины, кг; с – теплоемкость материала пластины, Дж/(кг·К);
Средняя по объему безразмерная температура пластины в момент времени τ при
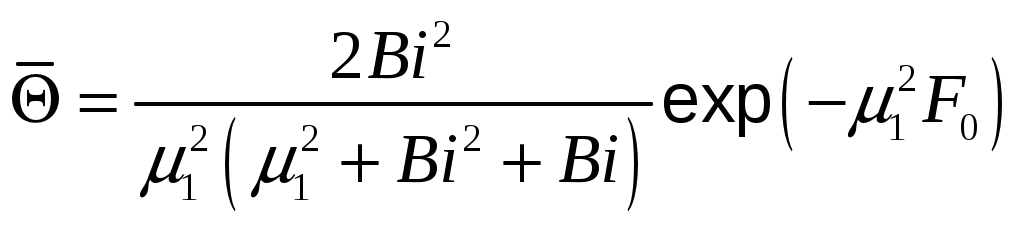 \
\Для цилиндрарадиусом
Средняя по объему безразмерная температура цилиндра в момент времени
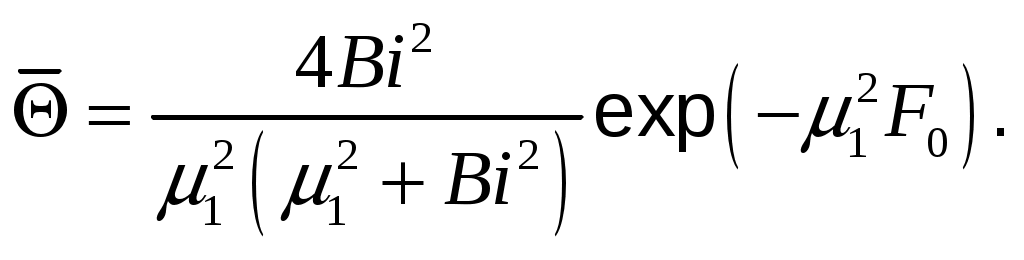
Тема 4. Конвективный теплообмен
Физическая сущность конвективного теплообмена. Формула Ньютона — Рихмана. Коэффициент теплоотдачи. Основы теории подобия. Критерии подобия и принцип их получения. Критериальное уравнение конвективного теплообмена. Определяющие и определяемые критерии подобия. Определяющая температура и определяющий линейный размер. Теплообмен при вынужденном движении жидкости или газа в трубах и каналах. Теплообмен при вынужденном поперечном омывании труб. Теплообмен при свободном движении жидкости. Теплообмен при изменении агрегатного состояния вещества.
Основные формулы для решения практических задач
Расчетные формулы для теплоотдачи при продольном обтекании пластины
При движении потока вдоль плоской поверхности, имеющей
для капельной жидкости
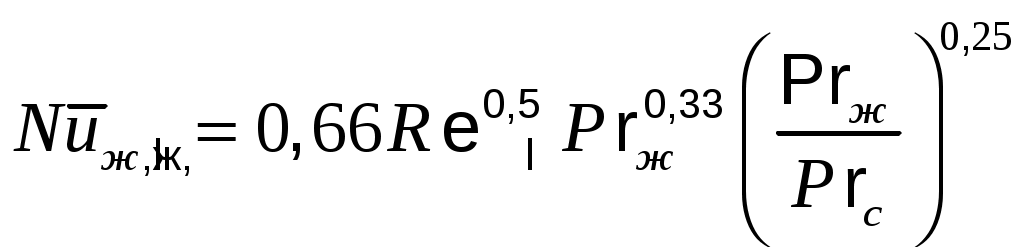
для воздуха
При турбулентномрежиме
для капельной жидкости
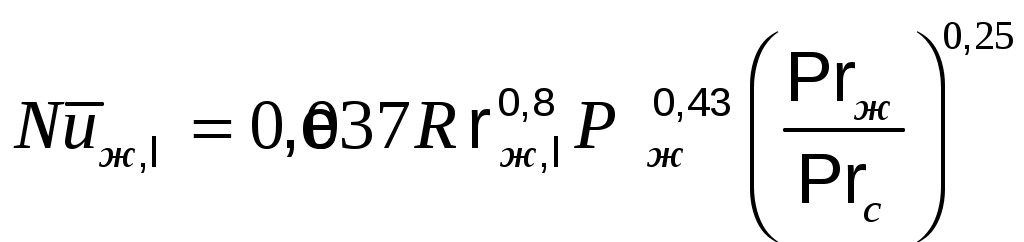
для воздуха
Определяющей принимается температура набегающего потока (
Местный коэффициент теплоотдачи на расстоянии х от передней кромки пластины определяется по формулам:
при ламинарном режиме течения в пограничном слое