Файл: Контрольная работа 1 Дисциплина Математическое моделирование систем и процессов Специальность Подвижной состав железных дорог.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 53
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО
ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Петербургский государственный университет путей сообщения
Императора Александра I» (ФГБОУ ВО ПГУПС)
Ярославский филиал ПГУПС
КОНТРОЛЬНАЯ РАБОТА № 1
Дисциплина: Математическое моделирование систем и процессов
Специальность: Подвижной состав железных дорог
Специализация: Грузовые вагоны
Форма обучения – ЗАОЧНАЯ
Вариант: 17
Выполнил: Поклонцев П.С. Шифр: 07-001-17-ПСя
Преподаватель: Гушель Н.П.
г. Ярославль
2023 г
Задание 1
Построить математическую модель механической системы, состоящей из пружины с жесткостью k=106 Н/м, один конец которой жестко закреплен, а на другом находится тело массой m=1.2 кг. Тело скользит по горизонтальному стержню: коэффициент трения скольжения µ=0.66.
Смещение тела из положения равновесия равно x0=9 см.
Найти: амплитуду, частоту и период свободных колебаний системы; частоту и период затухающих колебаний системы; уравнение огибающей кривой колебаний; смещение, скорость и ускорение тела в момент времени t=5 с для
затухающих колебаний.
Построить графики смещения свободных и затухающих колебаний системы в зависимости от времени.
Решение
Уравнение затухающих колебаний:

Уравнение огибающей кривой колебаний:
Смещение в момент времени 5 с.:
Скорость тела как производная от функции смещения:
Скорость тела в момент времени 5 с.:
Ускорение тела как производная от функции скорости:


Ускорение тела в момент времени 5 с.:
На рисунке 1 показан график смещения свободных колебаний.
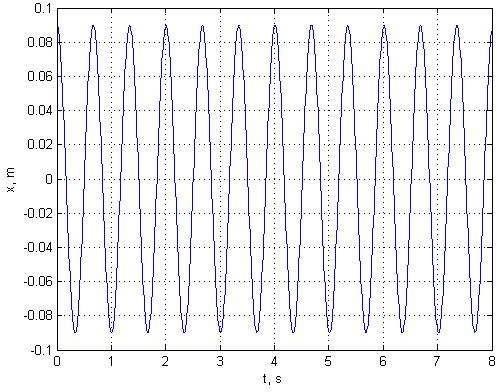
Рисунок 1 – Свободные колебания
На рисунке 2 представлен график смещения затухающих колебаний.
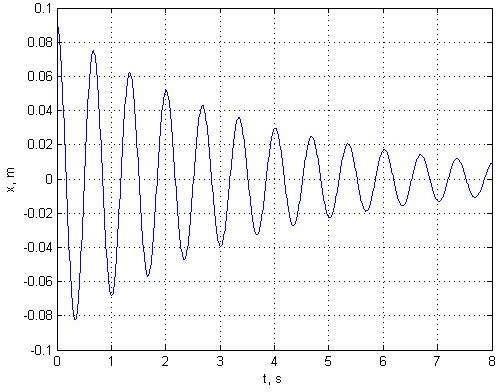
Рисунок 2 – Затухающие колебания
Задание 2
Подводная лодка водоизмещением V=1500 т движется горизонтально со скоростью υ=17 км/ч на глубине H=310 м от поверхности моря. Средняя плотность лодки ρ1. В момент t0=0 лодка начинает всплытие.
Сопротивлением воды пренебречь.
Определить:
время, когда лодка всплывет на поверхность моря; расстояние, которое пройдет лодка в горизонтальном направлении в
момент всплытия; вертикальную скорость лодки; траекторию движения подводной лодки в координатах l,h;
тип соответствующей кривой.
Плотность воды принять равной ρ0=103 кг/м3.
Решение Уравнение изменения глубины:
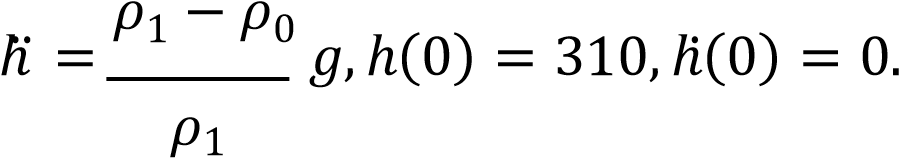
Зависимость вертикальной координаты движения лодки:
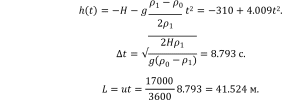
Вертикальная скорость лодки:
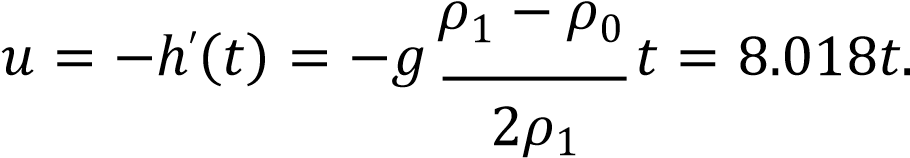
Траектория движения лодки:


Тип траектории – парабола.
На рисунке 3 изображена траектория движения.
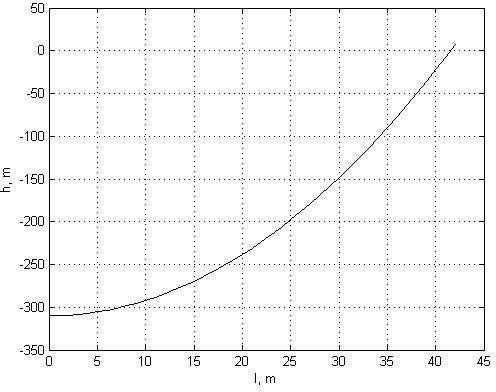
Рисунок 3 – Траектория движения подводной лодки
Задание 3
Канат длиной L=16 м и диаметром d=5.4 см лежит на плоской горизонтальной поверхности. Один конец его свободно свисает с поверхности вниз. Канат находится в состоянии равновесия. В некоторый момент времени канат начинает соскальзывать с поверхности под действием силы тяжести. Определить:
длину части каната, покоящуюся на поверхности, когда канат еще
находится в состоянии равновесия; закон движения каната;
скорость и ускорение каната в момент полного соскальзывания с
поверхности.
Плотность каната равна ρ=0.3·103 кг/м3. Коэффициент трения составляет k=0.2. Ускорение свободного падения принять равным g=10 м/сек2.
Решение
Равенство сил для части каната, лежащей на поверхности:
Равенство сил для другой части каната:
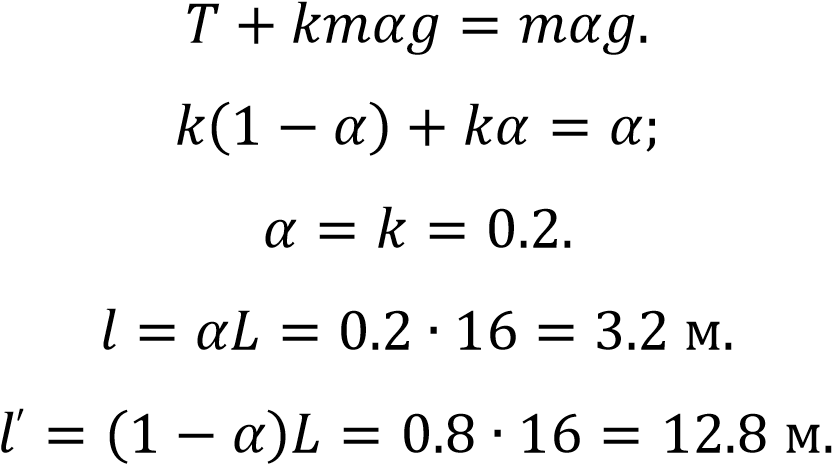
Ускоряющая сила – вес свободной части каната.
Уравнение движения каната:

Закон движения каната:

Начальные условия:
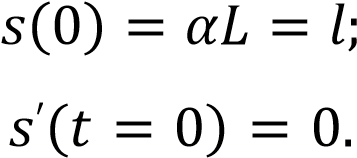
Момент полного соскальзывания каната с поверхности:
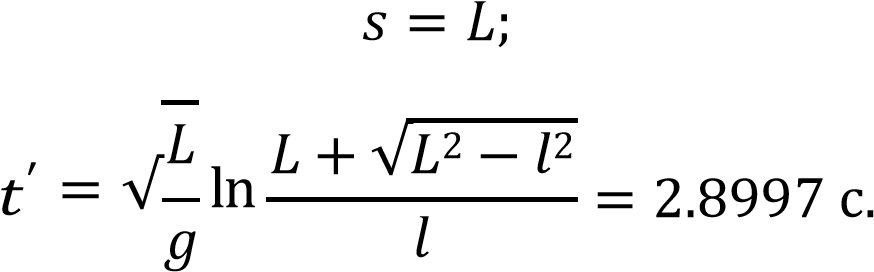

Скорость каната как производная от функции смещения:
????(????) = ????′(????) = 2.53????ℎ(0.791????).
Скорость каната в момент времени 2.8997 с.:
Ускорение каната как производная от функции скорости:
????(????) = ????′(????) = ????′′(????) = = 2????ℎ(0.791????).
Ускорение тела в момент времени 2.8997 с.:
Задание 4
На медной проволоке длиной l=1м и диаметром d=2.4 мм подвешена пустая емкость. В дне целиком заполненного водой цилиндрического бака высотой H=1 м и диаметром D=5 дм сделано отверстие круглой формы
диаметром d1=1.8 см, из которого вода перетекает в пустую емкость.
Найти:
объем V вытекающей из бака воды за время t; время, когда бак полностью опустеет; зависимость длины проволоки от времени: объем воды в емкости, длину проволоки и момент времени, в который
произойдет разрыв проволоки.
Предел прочности проволоки равен σ=2.2·108 Па. Плотность воды составляет ρ=103 кг/м3. Массой проволоки и емкости пренебречь.
Построить графики функций V=V(t) и l=l(t).
Решение Уравнение неразрывности:
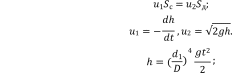
Объем вытекающей из бака воды как функция времени:
Объем бака:
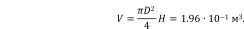
Время, когда бак полностью опустеет:
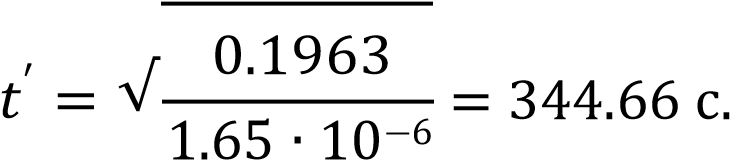

Зависимость длины проволоки от времени:

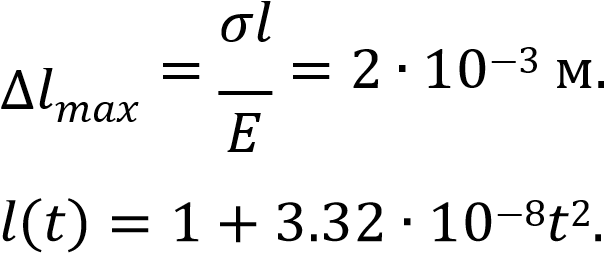
Момент времени, в который произойдет разрыв проволоки:
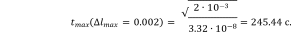
Объем воды в емкости в момент разрыва проволоки:
????емк = ????(????????????????) = ????(245.44) = 0.97 ∙ 10−1 м3.
Длина проволоки в момент разрыва:
????(????????????????) = ???? + ∆????(245.44) = 1.002 м.
На рисунке 4 показана зависимость объема вытекающей воды от времени.
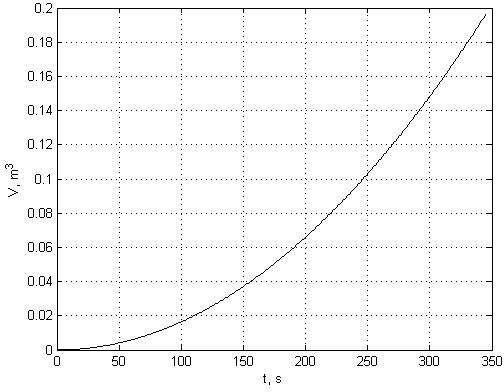
Рисунок 4 – Зависимость V(t)
На рисунке 5 представлена зависимость длины проволоки от времени.

Рисунок 5 – Зависимость l(t)
Задание 5
Пусть заданы координаты точек A(5;15) и C(30;5) плоскости. Точка B(x;0) лежит на прямой y=0.
Используя вариационные принципы построения математических моделей, найти:
условие, при котором ломаная ABC имеет наименьшую длину; числовое значение этого условия; наименьшую длину ломаной ABC.
Решение
Длина отрезка AB:
Длина отрезка BC:
Расстояние между точками A, B и C:
Задача представляет собой одномерную задачу безусловной оптимизации (поиска минимума функции ????). Условие, при котором ломаная ABC имеет наименьшую длину.
Для координаты ???? можно добавить дополнительное условие – искомая точка лежит между точками ???? и ????:
???? ∈ [−10; 20].
Найдем производную функции.

Найдем точку

Найдем минимальную длину ломаной:
???? = 36.056.
В дополнение построим график ????(????), который подтверждает
нахождение минимального значения длины ломаной (рисунок 6).
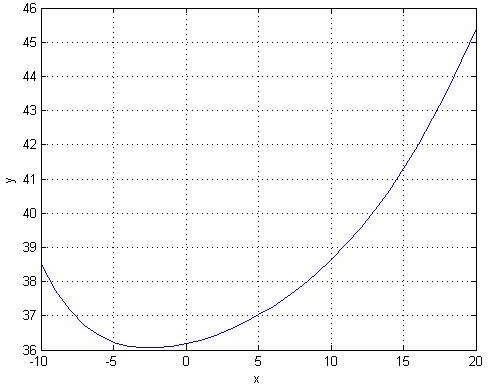
Рисунок 6 – Функция зависимости длины ломаной от координаты x точки B