Файл: Контрольная работа 1 По дисциплине теория электросвязи Группа Шифр Вариант 3 Проверил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 81
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ф
ГБОУ ВО СибГУТИКолледж телекоммуникаций и информатики
КОНТРОЛЬНАЯ РАБОТА №1
По дисциплине: теория электросвязи
Выполнил:
Группа:
Шифр:
Вариант: 3
Проверил: _______________
Новосибирск, 2016 г.
Содержание:
1. Задача №13
2. Задача №210
3. Задача №315
4. Задача №420
5. Задача №523
6. Список использованной литературы31
Задача №1.
1. Дайте определение понятия «электрический сигнал». Приведите классификацию сигналов. Перечислите формы представления сигналов.
2. Начертите временные диаграммы двух периодических сигналов прямоугольной формы с заданными в Таблице 1 параметрами. Запишите уравнения временных функций заданных сигналов.
3. Рассчитайте амплитуды составляющих спектра заданных сигналов. Начертите спектральные диаграммы. Запишите уравнения спектральных функций заданных сигналов.
4. Дайте определение понятия «ширина спектра сигнала». Укажите ширину спектра для каждого из заданных сигналов. Поясните зависимость ширины спектра периодической последовательности прямоугольных импульсов от длительности импульса.
Таблица 1 – Исходные данные
| Параметры | Вариант 3 |
| Длительность импульса tИ1, мс | 0,2 |
| Длительность импульса tИ2, мс | 0,33 |
| Период следования импульсов Т, мс | 1 |
| Амплитуда импульсов Um, В | 10 |
Решение:
1. Электрический сигнал – это электромагнитное колебание один или несколько параметров которого изменяясь во времени и пространстве отображают передаваемое сообщение.
Сигналы классифицируются:
1 классификационный признак – вид физического явления, используемого в роли носителя информации: заряд, ток, напряжение, звуковое давление, интенсивность света. При рассмотрении сигналов в радиотехнических устройствах в роли носителя информации рассматривается ток (I) или напряжение (U), зависящее от времени (t) или частоты (f). При
этом различают аналоговые, импульсные и случайные сигналы.
Аналоговый сигнал – сигнал, значение которого в каждый момент времени может быть точно предсказано (измерено).
Импульсный сигнал – представляет собой сигнал, существующий лишь в пределах конечного отрезка времени.
2 классификационный признак – размерность пространства, в котором существует сигнал. Например, ток или напряжение в большинстве радиотехнических устройств можно рассматривать как одномерный сигнал, зависящий от времени. Распределение токов и напряжений в длинной линии представляет собой сигнал, зависящий от двух переменных: времени и пространства.
Сигналы могут быть разделены на детерминированные и случайные (стохастические).
Детерминированными сигналами называются сигналы, значения которых в любые моменты времени являются известными величинами или могут быть заранее вычислены. Математическая модель детерминированных сигналов позволяет предсказывать их мгновенные значения в любые моменты времени.
Случайные (стохастические) сигналы представляют сигналы, мгновенные значения которых являются случайными величинами. Анализ этих сигналов основан на теории вероятностей и теории случайных процессов.
Рисунок 1 – временная диаграмма периодического сигнала 1 прямоугольной формы с заданными параметрами в Таблице 1.
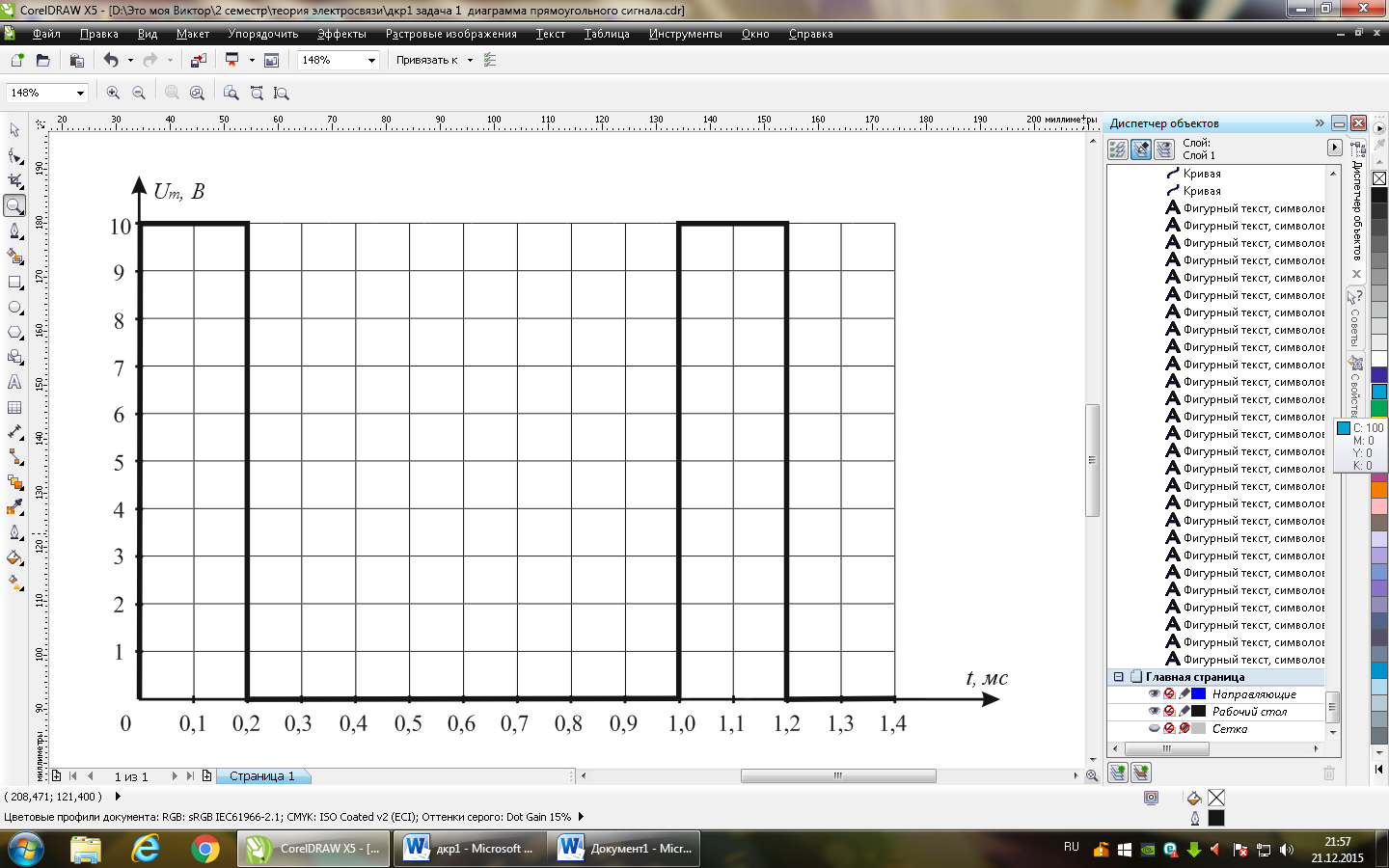
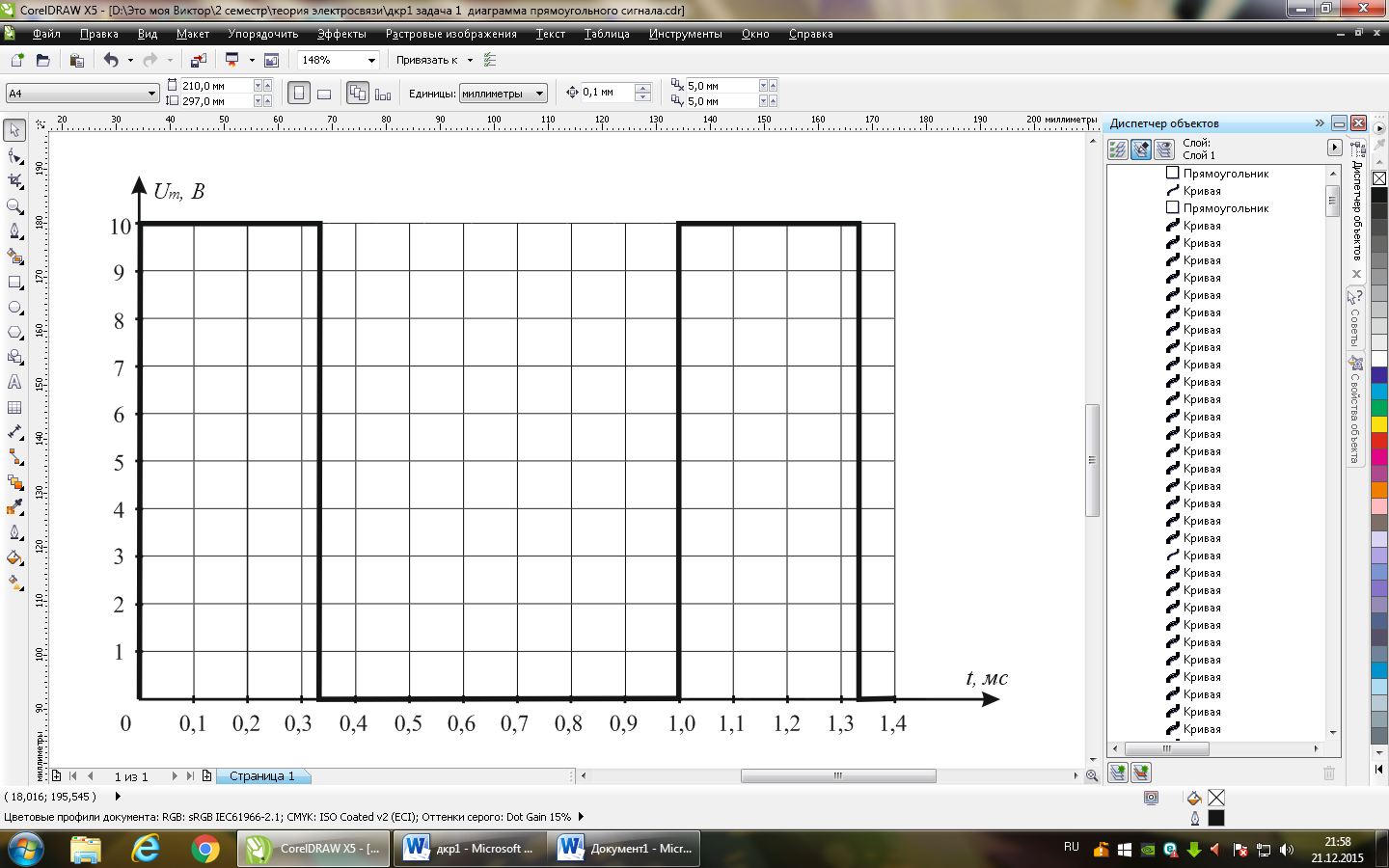
Рисунок 2 – временная диаграмма периодического сигнала 2 прямоугольной формы с заданными параметрами в Таблице 1.
2.2. Уравнения временных функций
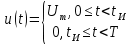
Уравнения временных функций заданных сигналов
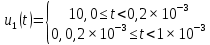
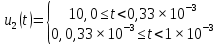
3.1. Формулы для расчета амплитуд составляющих спектра:
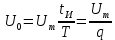
где q – скважность периодической последовательности прямоугольных импульсов,
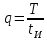
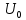– постоянная составляющая сигнала,
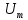– амплитуда импульсов,
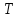– период следования импульсов,
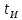– длительность импульса,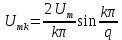
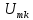– амплитуда k-й гармоники сигнала,
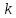– номер гармоники,3.2. Расчет скважности:
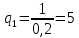
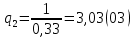
Таблица 2 – расчеты амплитуд спектра
| № гармоники | 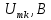 | № гармоники | |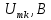
| 0 | 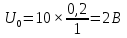 | 0 |  |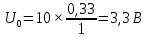
| 1 | 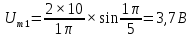 | 1 |  |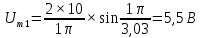
| 2 | 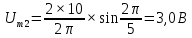 | 2 |  |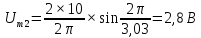
| 3 | 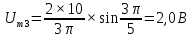 | 3 |  |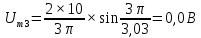
| 4 | 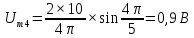 | 4 |  |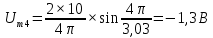
| 5 | 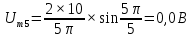 | 5 |  |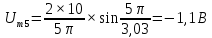
| 6 | 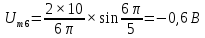 | 6 |  |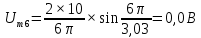
| 7 |  | | |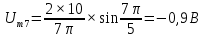
| 8 |  | | |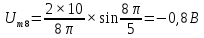
| 9 |  | | |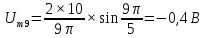
| 10 |  | | |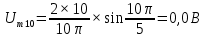
Рисунок 3 – спектральная диаграмма сигнала 1
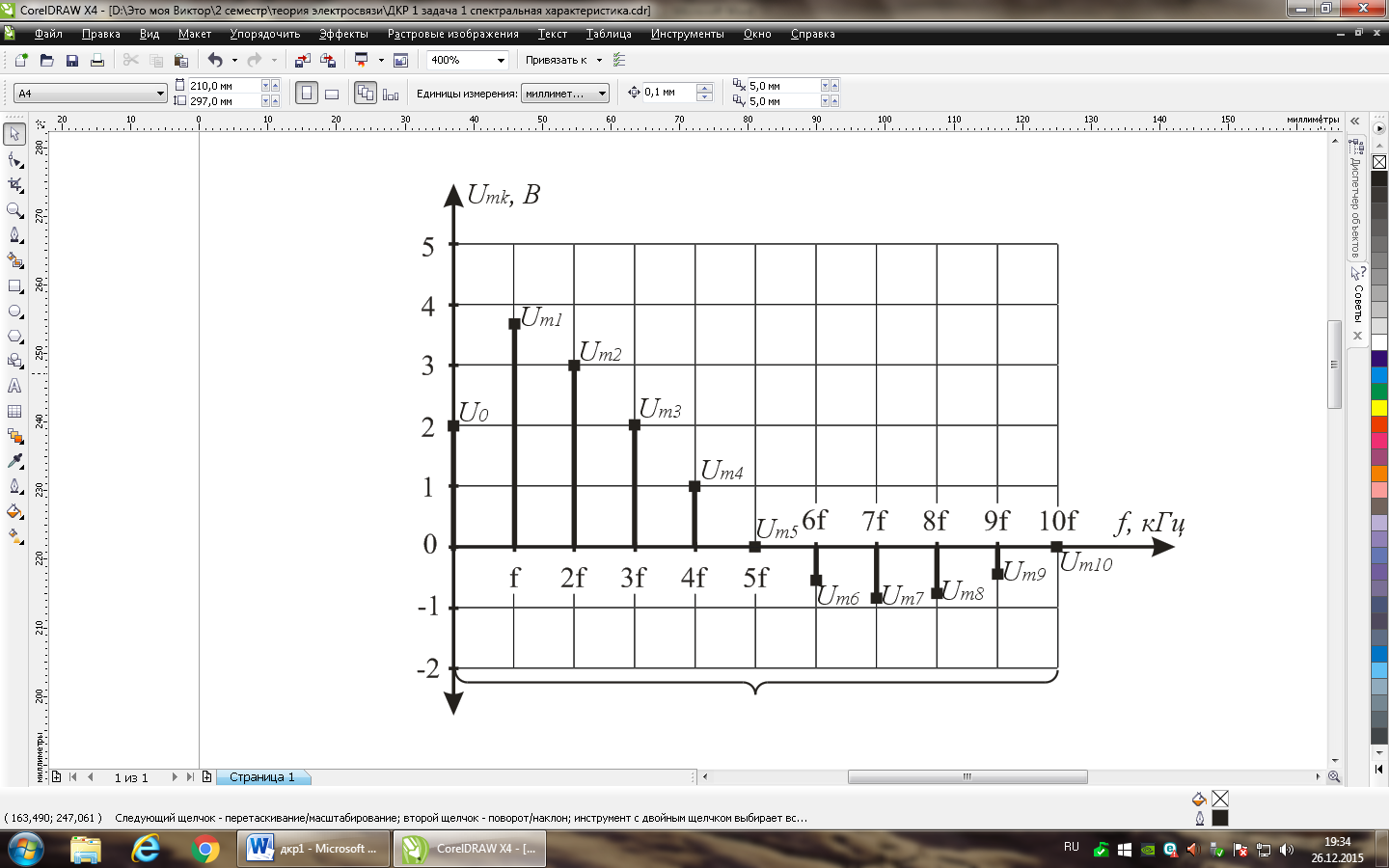
Рисунок 4 – спектральная диаграмма сигнала 2
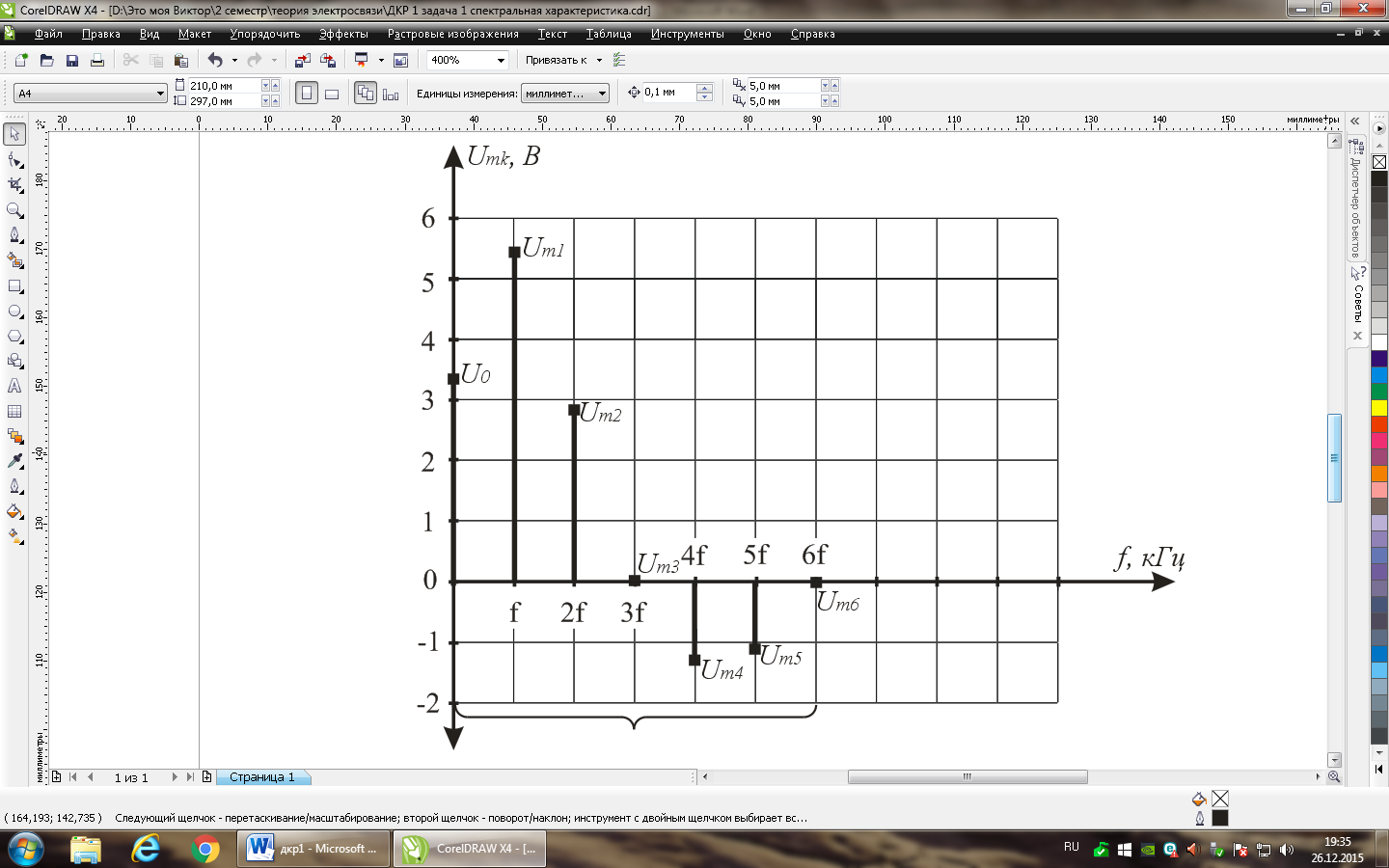
3.4. Уравнение спектральной функции:
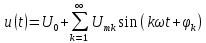
Уравнения спектральных функций заданных сигналов:
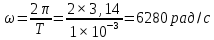
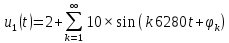
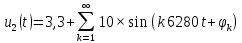
4. За ширину спектра сигнала
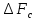принимают диапазон частот, в котором сосредоточено (90-95)% энергии сигнала. При уменьшении длительности импульса tИ ширина спектра сигнала
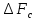увеличивается.Задача №2.
1. Дайте определение понятия «нелинейная цепь». Поясните суть аппроксимации характерист
4. Начертите график спектральной характеристики тока в цепи. Поясните спектральный состав тока в цепи.
Решение:
1. Под нелинейной электрической цепью понимают цепь, в которой имеется один или несколько нелинейных элементов. Отклик нелинейного элемента не пропорционален приложенному воздействию и, следовательно, график его основной характеристики – нелинейный. Примером может служить ВАХ полупроводникового диода. При прохождении сигнала по такой цепи возникают нелинейные искажения, то есть изменяется форма сигнала и его спектральный состав. Принцип действия устройств, выполняющих спектральные преобразования сигналов (умножителей частоты, модуляторов, детекторов) основываются на свойствах нелинейных элементов.
Аппроксимация – приближенная замена реальной характеристики нелинейного элемента его математической моделью.
2. Гармонический анализ нелинейной цепи – это определение амплитуд частотных составляющих спектра отклика цепи. Для выполнения расчета составляющих спектра необходимо знать уравнение, описывающее нелинейную характеристику.
При полиноминальной аппроксимации вольт-амперная характеристика нелинейного элемента представляется степенным полиномом n – степени вида i = a0 + a1u + a2u2 + a3u3 + … + anun. Наиболее часто для аппроксимации используется полином второй (n = 2) или третей (n = 3) степени.
Таблица 4 – составляющие спектра тока в нелинейной цепи
| Название | Частота | Формулы для расчета амплитуды тока |
| Постоянная составляющая | 0 |  |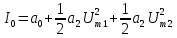
| Первые гармоники | f1 |  |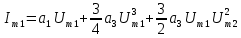
| f2 |  | |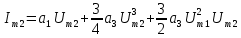
| Вторые гармоники | 2f1 |  |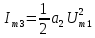
| 2f2 |  | |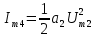
| Третьи гармоники | 3f1 |  |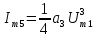
| 3f2 |  | |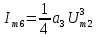
| Комбинационные составляющие 2 порядка | f1 – f2 |  |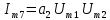
| f1 + f2 |  | |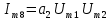
| Комбинационные составляющие 3 порядка | 2f1 – f2 |  |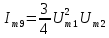
| 2f1 + f2 |  | |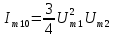
| f1 – 2f2 |  | |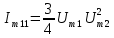
| f1 + 2f2 | 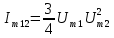 |