ВУЗ: Омский государственный технический университет
Категория: Учебное пособие
Дисциплина: Методы оптимальных решений
Добавлен: 12.02.2019
Просмотров: 1241
Скачиваний: 4
продукции вторых, в этом варианте расчета удобнее пользоваться не
матричной формой модели (10.6), а системой линейных уравнений
(10.5).
Пусть
B
A
E
1
)
(
, тогда
BY
X
(10.9)
Или
j
n
i
ij
i
Y
X
1
,
n
i
,
1
(10.10)
Коэффициенты
ij
называются
коэффициентами полных
материальных затрат и включают в себя как прямые, так и косвенные
затраты всех порядков.
Определение 2. Коэффициенты полных материальных затрат
показывает, какое количество продукции i–ой отрасли нужно
произвести, чтобы с учетом прямых и косвенных затрат этой продукции
получить единицу конечной продукции j–ой отрасли.
Анализ модели МБ приводит к следующим выводам:
а)
0
А
– по определению;
б)
1
ij
, т.к. процесс воспроизводства нельзя было бы
осуществлять, если бы для собственного воспроизводства в отрасли
затрачивалось большее количество продуктов, чем создавалось;
в)
0
X
– из содержательных систем
ij
x
.
Определение 3. Матрица
0
А
называется продуктивной, если
существует такой
0
Х
, что
АХ
Х
. Отсюда следует, что для
продуктивной матрицы
А
из (10.6) существует положительный вектор
конечной продукции
0
Y
.
Для того, чтобы матрица
А
была продуктивной, необходимо и
достаточно, чтобы выполнялось одно из перечисленных ниже условий.
1) матрица
1
)
(
A
E
неотрицательно обратима, т.е. существует
обратная матрица
0
)
(
1
A
E
.
2) матричный ряд
0
3
2
...
k
k
A
A
A
A
E
сходится, причем его
сумма равна
1
)
(
A
E
.
3) наибольшее по модулю собственное значение
матрицы
А
, т.е.
решения характеристического уравнения
0
А
Е
строго меньше единицы
4) все главные миноры матрицы
)
(
А
Е
, порядка от 1 до n
положительны.
Замечание. Более простым, но только достаточным признаком
продуктивности матрицы является следующий признак
1
А
, т.е. если
величина наибольшего из сумм ее элементов в каждом столбце < 1, то
матрица
А
продуктивна.
9.2Модель равновесных цен
X – валовая продукция
Y – конечная продукция
P - вектор цен
Затраты:
x1p1=x1(a11p1+a21p2+…..+an1pn)+V1
V1 – непроизводственные расходы
Можно сократить:
p1=a11p1+a21p2+…..+an1pn + v1/x1
v1/x1 = u - норма добавленной стоимости, т е величина добавленной
стоимости на единицу продукции
P=A
T
P+V – вектор норм добавленной стоимости
Прогноз цен на продукцию отраслей при известной стоимости:
P-A
T
P=V
(E-A
T)
P=V
P=(E-A
T
)
-1
=V
Модель международной торговли
Имеется n стран s1….sn
aij-доля торгового бюджета страны, которая тратится на покупку товара
в стране.
Торговый бюджет можно условно принять за единицу.
Сумма а=1, т е сумма элементов столбца матрицы торговли = 1.
Выручка страны:
pi=ai1x1+ai2x2+….+ainxn
pi=xi
AX=X, AX-EX=0
(A-E)X=0
X – собственный вектор марицы А, соотв собств числу =1
10. Управление в системах
11.1. Общие принципы управления
Управление – это функция системы, направленная либо на
сохранение основного качества системы, либо на выполнение
некоторой
программы,
обеспечивающей
устойчивость
функционирования, либо на достижение определенной цели.
Система, в которой реализуется функция управления, называется
системой управления.
В системах управления можно выделить две подсистемы:
управляющую (осуществляющую функцию управления) и управляемую
(объект управления).
В технических системах управляющую подсистему часто называют
системой регулирования.
В социально – экономических используют термин – система
организационного управления.
В сложных развивающихся системах эти блоки могут быть
совмещены. Такой режим называют саморегулированием.
Если управление осуществляется сознательно, то управляющая
система называется субъектом управления, который формирует цель
управления.
Для использования процессов управления в технических системах
разработана теория автоматического управления (ТАУ). В ней
разработаны общие принципы управления. Основные из них:
1)
Принцип разомкнутого (программного) управления.
Представлен на рис.11.1.
Рис. 11.1.
здесь x (t) – закон функционирования
u (t) – управляющее воздействие
Zj – помехи
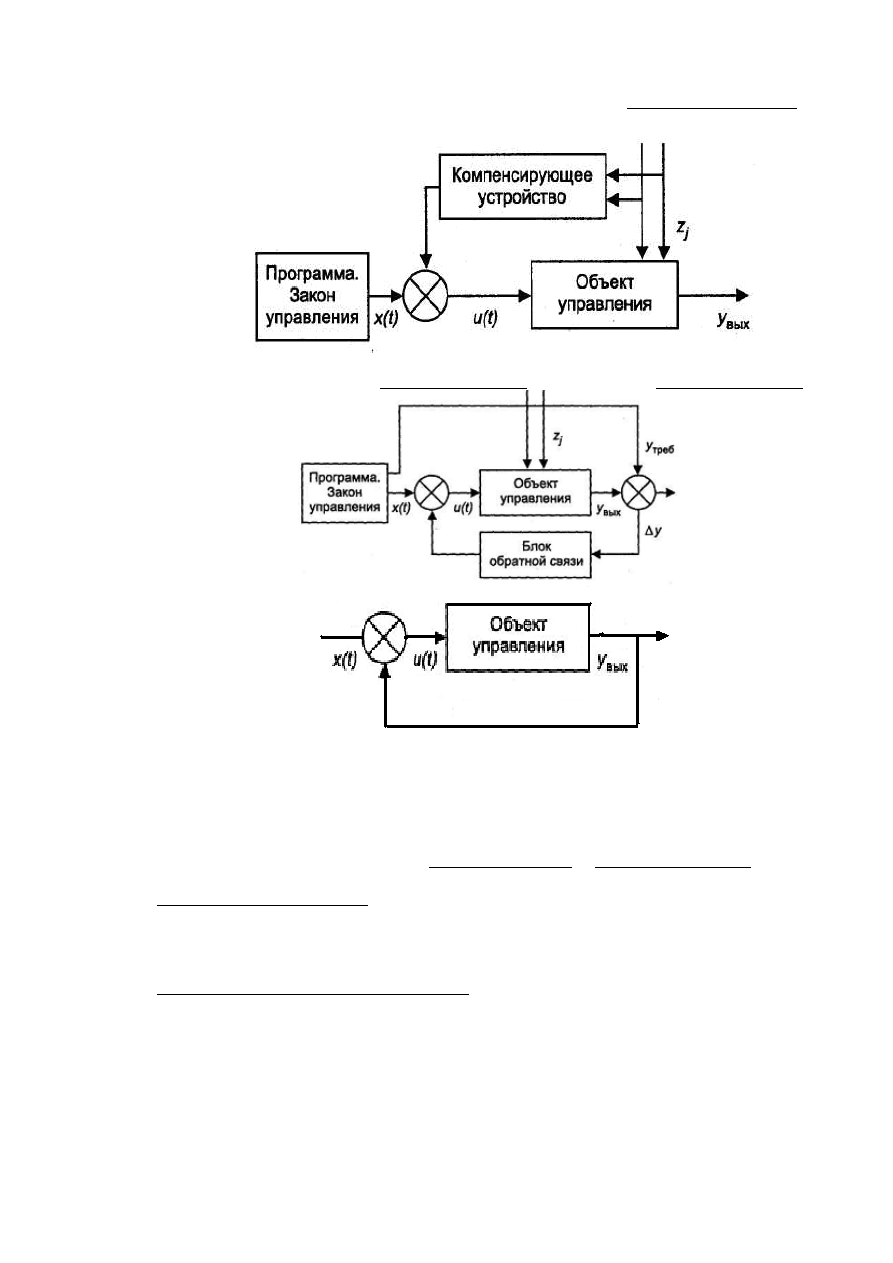
2)
Принцип компенсации или управление по возмущениям (с
упреждением).
3)
Принцип обратной связи (управление по отклонению),
«следящая система»
Самый простой пример системы с обратной связью – «следящая»
система (ПВО – системы наведения на цель), (рис. 11.3 б).
Обратная связь может быть отрицательной и положительной.
Отрицательная связь – противодействует тенденциям изменения
выходного параметра, т.е. направлена на сохранение, стабилизацию
требуемого значения параметра (количество выпускаемой продукции).
Положительная обратная связь – сохраняет, усиливает тенденции
происходящих
в
системе
изменений
выходного
параметра
(развивающиеся системы).
4)
Совмещение принципов обратной связи с управлением по
возмущением. Такие модели являются основой адаптационного
управления, (рис. 11.4)
Рассмотренные принципы управления в той или иной форме
используются в различных областях управления (ТАУ, АУ) – от
регулирования в технических системах до управления коллективами
людей (менеджмент).
11.2. Управление в социально – экономических системах
Для этих сфер разрабатывают более конкретные принципы
управления, формы и методы их реализации. Приведем примеры
некоторых из них:
1) Введение правил взаимоотношения между людьми (правил
этики, законов религии, светских законов и правовых норм) –
«правовое государство».
2) Административно
– бюрократическое управление –
«тоталитарное государство».
3) Управление с помощью целеобразования – основан на
принципах самоорганизации – характерен для творческих
профессий, часто проявляется во время войн, стихийных бедствий,
кризисов – «Этапы строительства социализма».
Первые два способа основаны на принуждении (административном,
либо с помощью законов).
Основы третьего способа – способность человека, предприятия,
региона и т.д. к самоорганизации.
11. Устойчивость систем
1. Общие положения. Равновесие систем
Под устойчивостью экономических систем понимается способность
системы возвращаться в состояние экономического равновесия, после
того она была из этого состояния выведена под влиянием внешних или
внутренних возмущающихся воздействий.
Тогда экономические реформы могут быть интерпретированы как