Федеральное государственное образовательное бюджетное учреждение
высшего образования

«ФинансоВЫЙ УНИВЕРСИТЕТ

при Правительстве Российской Федерации»

(Финансовый университет)
Департамент математики


Домашняя Контрольная работа
по дисциплине
«Эконометрические исследования»
на тему: «Линейная модель множественной регрессии»

Выполнил:

студент группы БА21-1м

Акбашев А.Д.

Проверил:

к.э.н., доцент Данеев О.В.

Оценка: _____________________________

Москва – 2022
Цель данной работы оценить линейную модель множественной регрессии. В работе будет проведено:

1. 
   Проверка адекватности модели
   
2. 
   Проверка значимости регрессеров
   
3. 
   Проверка выполнения предпосылок теоремы Гаусса-Маркова на гомоскедастичность и отсутствие автокорреляции.
   

Анализ был проведен в MS Excel. Для работы были подобранны данные о влиянии на урожайность зерновых культур количества тракторов приведенной мощности на 100 га, количества зерно-уборочных комбайнов на 100 га, количества удобрений, расходуемых на 1 га и количества химических средств защиты на 1 га.

Район	Урожайность зерновых культур Y	Число тракторов приведённой мощности на 100 га Х1	Число зерно-уборочных комбайнов на 100 га Х2	Количество удобрений, расходуемых на 1 га, Х3	Количество химических средств защиты на 1га, Х4
1	9,70	1,59	0,25	0,32	0,14
2	9,95	0,46	0,26	0,77	0,66
3	8,40	0,28	0,29	0,59	0,46
4	8,78	1,13	0,27	0,55	0,64
5	10,50	0,64	0,24	0,76	0,82
6	11,20	0,59	0,31	0,99	0,89
7	12,00	0,73	0,27	0,64	0,20
8	10,01	1,34	0,27	0,38	0,35
9	9,67	1,06	0,28	0,48	0,42
10	9,55	1,33	0,26	0,62	0,51
11	10,30	0,95	0,23	0,81	0,44
12	11,60	0,86	0,28	0,75	0,37
13	12,40	0,97	0,27	0,46	0,28
14	11,30	1,05	0,26	0,42	0,19
15	12,10	1,38	0,26	0,57	0,30

---

В первую очередь был проведен анализ на адекватность модели с константой и без неё. Была использована функция «линейн» для обоих случаев. Для модели с константой ( 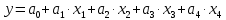) были получены следующие данные:

	а4	а3	а2	а1	а0
	-4,203826369	5,03649386	6,48641417	0,30928251	7,2037886
S	2,071225077	2,8820627	17,0682433	1,21861409	5,48996428
R	0,335969839	1,15849032	#Н/Д	#Н/Д	#Н/Д	СКО
F-тест	1,138400305	9	#Н/Д	#Н/Д	#Н/Д	Число степеней свободы
	6,111387362	12,0788984	#Н/Д	#Н/Д	#Н/Д
	RSS	ESS

Прогнозное значение	10,9267197
Контролирующее	12,10
Разница	1,17328026

Для проверки было посчитано прогнозное значение

---

, далее посчитана разница между Y последнего значения и прогнозным. Полученный результат сравниваем с СКО, в данном случае СКО < Разницы, следовательно модель неадекватна.
То же самое было сделано для модели без константы ( 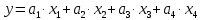) и были получены следующие результаты:

	а4	а3	а2	а1	а0
	-4,564560455	6,63259102	26,9293198	1,29102365	0
S	2,125697862	2,7054514	7,21908256	0,99600849	#Н/Д
R	0,990579202	1,19957187	#Н/Д	#Н/Д	#Н/Д	СКО
F-тест	262,8702925	10	#Н/Д	#Н/Д	#Н/Д	Число степеней свободы
	1513,052673	14,3897268	#Н/Д	#Н/Д	#Н/Д
	RSS	ESS

Прогнозное значение	11,1944445
Контролирующее	12,10
Разница	0,90555546

В этом случае получается обратный результат СКО > Разницы, что

---

говорит нам о том, что модель адекватна.

Как стало понятно из предыдущих расчетов, для анализа была взята модель без константы. Далее проверяем значимость полученного уравнения регрессии. С помощью той же функции «линейн» получаем следующие результаты:

	a4	a3	a2	a1	a0
	-4,804211164	7,04400594	25,8315572	1,51205212	0
S	2,043252363	2,56973455	6,85695468	0,91700261	#Н/Д
R	0,991011899	1,16948917	#Н/Д	#Н/Д	#Н/Д	СКО
F-тест	303,2100753	11	#Н/Д	#Н/Д	#Н/Д	Число степеней свободы
	1658,807646	15,0447541	#Н/Д	#Н/Д	#Н/Д
	RSS	ESS

F критическое при  = 0,05, m = 4, n=15, const = 0 составляет 3,36. Сравниваем F-тест и F-критическое и видим, что первое больше второго, а это значит, что уравнение регрессии статистически значимо.

Далее проверяем значимость всех коэффициентов регрессии. Были посчитаны t для всех коэффициентов по формуле:

---

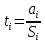
t-критическое = 2,2 ( при  = 0,05, m = 4, n=15, const = 0)

t1	1,648907103
t2	3,767205482
t3	2,741141463
t4	2,351256874
t критич	2,20098516

Все полученные t сравниваем с t-критическое и делаем выводы, что все Х кроме 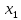статистически значимы, так как они больше, чем t-критическое.

После этого были найдены доверительные интервалы для коэффициентов регрессии:

	нижняя граница	верхняя граница
интервал для а1	-0,50625702	3,530361259
интервал для а2	10,73950176	40,92361273
интервал для а3	1,388058317	12,69995356
интервал для а4	-9,301379292	-0,307043035

Предыдущий вывод, что все коэффициенты кроме 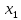статистически значимы, так как у них 0 не попадает под интервал верхней и нижней границы. Так как 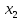, , 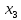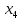статистически значимы была построена и оценена модель для Y и этих коэффициентов:

	a4	a3	a2
	-5,311898195	5,80066559	34,85988699	0
S	2,159749528	2,62667393	4,413510073	#Н/Д
R	0,98879029	1,250446576	#Н/Д	#Н/Д	СКО
F-тест	352,8335012	12	#Н/Д	#Н/Д	Число степеней свободы
	1655,089	18,76339968	#Н/Д	#Н/Д
	RSS	ESS

---

Смотрите также файлы

• Программа Порфирьевич.docx

• Бактериурия Выполнила Ильясханова Э. С.pptx

• Общественное здоровье и здравоохранение история развития науки История становления.pptx

• Пояснительная записка настоящая программа предусматривает изучение детьми материала по теории и истории шашек, участие в соревнованиях, организационно судейскую практику..docx

• 1. Дайте определение организации и перечислите функции организаций в национальной экономике. Организация.docx