Файл: Линейная модель множественной регрессии.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 60

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


F-критическое изменится, так как у нас поменялось количество Х и составит 3,49 (при  = 0,05, m = 3, n=15, const = 0).

Также сравниваем F-тест и F-критическое. F-тест больше, как и в прошлом варианте, а это значит, что уравнение регрессии статистически значимо.

Далее была проведена проверка предпосылок Гаусса-Маркова. С помощью теста Голдфельда-Квандта проведена проверка на гомоскедастичность. Чтобы провести данную проверку исходные данные были разделены на 3 равные части по 5. В первой части мы получили ESS равный 0,750878, а третьей части 0,002836. Для проверки гипотезы были введены случайные переменные GQ1 = 264,8 и GQ2 = 0,004. F-критическое при при  = 0,05, m = 2, n=5, const = 0 равен 161,5. F-критическое больше GQ2, но меньше чем GQ1, а это значит, что гипотеза о гомоскедастичности не выполняется соответственно модель имеет гетероскедастичность.

Необходимо побороть гетероскедастичность. Для этого проведем визуальный анализ графика остатков:

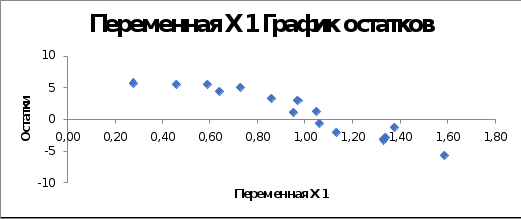
Видим, что по графику у переменной Х1 наибольший разброс, поэтому, чтобы побороть гетероскедастичность выбираем его. Для этого посчитаем дополнительные показатели:


p=1+x1
y*=y/p
x0*=1/p
x1*=x1/p

2,59
3,75
0,39
0,61

1,46
6,82
0,68
0,32

1,28
6,56
0,78
0,22

2,13
4,12
0,47
0,53

1,64
6,40
0,61
0,39

1,59
7,04
0,63
0,37

1,73
6,94
0,58
0,42

2,34
4,28
0,43
0,57

2,06
4,69
0,49
0,51

2,33
4,10
0,43
0,57

1,95
5,28
0,51
0,49

1,86
6,24
0,54
0,46

1,97
6,29
0,51
0,49

2,05
5,51
0,49
0,51

2,38
5,08
0,42
0,58


После этого находим также ESS в первой и третьей части. ESS1 = 1,22, ESS2 = 0,61. После этого находим F-критическое и показатели GQ1 и GQ2:


F-критич
6,38823291

GQ1
2,01150283

GQ2
0,49714074

F-критическое больше обоих показателей, значит условие о гомоскедастичности выполняется.

Так как концентрация значений больше у первой переменной, то для

В конце была проведена проверка на автокорреляцию с помощью статистки Дарбина-Уотсона. Для этого нам надо посчитать DW = 26,04/15,04 = 1,73. Значения границы при k=4 составляют 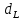= 0,69 и 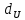= 1,97. DW находится в области неопределенности в точке между 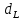и 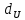, а это значит, что нельзя определить есть автокорреляция или нет.

Смотрите также файлы