Файл: Физика изучение спектра излучения атома водорода Методические указания к лабораторной работе Электронный учебный материал Минск 2020.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 153
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
n
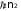E e n e 0
2 32 2 2
(8)
и потенциальной энергии кулоновского взаимодействия электрона с ядром
e2 me4
0
Un e
(9)
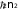40rn
16 2 2
Итак, с учетом (8) и (9), получаем важную формулу теории Бора - формулу квантования энергии электрона в атоме водорода
кин
me4
me4
13,6
En En
Un e e
эВ (10)
32 2 2 2n2 8 2h2n2 n20 0
Таким образом, полная энергия электрона в атоме является отрицательной, так как, по определению, отрицательна потенциальная электростатическая энергия взаимодействия электрона с ядром. С ростом номера орбиты полная энергия электрона в атоме возрастает. При этом номер орбиты n является квантовым числом в теории Бора. Если заряд ядра водородоподобных атомов (т.е. систем с положительно заряженным ядром
и одним электроном на оболочке: H, He+, Li++ и т.д.) равен Z, то полная энергия электрона в таких атомах
имеет вид
me4Z2
En e . (11)
0
8 2h2n2
На рисунке 5 в соответствии с (10) представлен энергетический спектр электрона в атоме водорода. В области положительных энергий энергетический спектр свободного электрона является сплошным спектром, т.е. энергия электрона в этом случае не является квантованной величиной и его поведение описывается в рамках классической физики. В области отрицательных значений полной энергии энергетический спектр связанного с атомом электрона становится дискретным. Для наглядности на рисунке 5 каждому возможному значению энергии соответствует энергетический уровень. В стационарном состоянии электрон может находиться на одном из этих дискретных энергетических уровней.
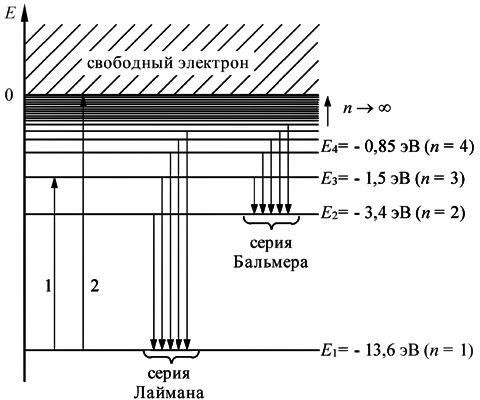
Рисунок 5. Энергетический спектр атома водорода
Переход электрона с одного уровня на другой (обусловленный изменением энергии электрона) изображен соответствующей стрелкой, начало и конец которой указывают энергетические уровни, между которыми происходит переход.
Обычно атом находится в основномсостояниис наименьшим значением энергии, равным E1(т.е. при n=1). В этом состоянии атома электрон движется по первой стационарной орбите, имеющей минимальный радиус, равный боровскому радиусу a. Если атому (т.е. электрону) сообщить дополнительную энергию, то атом может перейти в возбужденноесостояние(см. например, переход 1 на рисунке 5). Электрон
при этом переходит на орбиту большего радиуса. К возбуждению атомов могут приводить различные процессы: столкновение атомов при хаотическом тепловом движении, пропускание через газ потока высокоэнергетических частиц (электронов, альфа-частиц и др.), отдающих энергию при соударении с атомами, и, наконец, поглощение атомами электромагнитного излучения в широкой области спектра.
Если энергия, переданная электрону, будет достаточно велика, тоон может преодолеть силу притяжения к ядру и оторваться от атома,т.е.происходитпроцесс,называемыйионизациейатома. Энергиейионизацииназываютнаименьшуюэнергию,необходимуюдляудаленияэлектрона из свободного атома в его низшем энергетическом состояниинабесконечность.
Из рисунка 5 видно, что минимальная энергия, необходимая дляионизации атома водорода (переход 2), равна
Eион E E1 E1
13,6 эВ,
что хорошо согласуется с экспериментальными данными.
Как и любая физическая система, атом стремится занять состояние с наименьшей энергией, т.е. в возбужденном состоянии, характеризующимся большей энергией, он долго находиться не может. Поэтому через время 10- 8 с возбужденный атом самопроизвольно (спонтанно) переходит в состояние с меньшей энергией, испуская при переходе фотон. Такой процесс продолжается до тех пор, пока атом не окажется в основном состоянии.
Набор спектральных линий, соответствующих излучению атома, возникающему при всевозможных переходах с понижением энергетического уровня называют спектромизлученияатома.
-
Спектральныесерииатомаводорода
Итак, если установлена структура энергетических уровней атома водорода, то согласно второму постулату Бора можно рассчитать и частоты спектральных линий спектра излучения этого атома, используя правило частот (формула 2) и выражение для энергии состояний (формула 10):
m
e4 1
1
nk e ,
n k. (12)
0
8 2h3 k2
n2
Так как частота и длина волны связаны соотношением =с/ (с - скорость света в вакууме), то для определения длин волн соответствующих переходов формула (12) преобразуется к виду:
1 R 1
1
(13)
k2 n2
nk
где R–постоянная Ридберга, равная
me 7
4
0
Re 1,097 10 8 2h3c
м1
. (14)
Из уравнений (12) и (13) следует, что при заданных значениях kи меняющихся значениях n (n k, см. рисунок 5) спектральные линии образуют группы или серии. Как видно из (13) в спектре излучения атома водорода можно выделить следующие спектральные серии (экспериментально наблюдавшиеся еще до появления теории Бора):
СерияЛаймана(ультрафиолетовая область спектра), соответствует переходам электрона на первый энергетический уровень со всех вышестоящих:
1 R 1 1 , где n=2,3,4,… (15)
12 n2
n1
СерияБальмера(видимая область спектра), соответствует переходам электрона на второй энергетический уровень со всех вышестоящих:
1 R 1
1 , где n= 3,4,5,… (16)
22 n2 n2
СерияПẚшена(инфракрасная область спектра), соответствует переходам электрона на третий энергетический уровень со всех вышестоящих:
1 R 1 1 , где n= 4,5,6,… (17)
32 n2
n3
СерияБреккета(далекая инфракрасная область спектра), соответствует переходам электрона на четвертый энергетический уровень со всех вышестоящих:
1 R 1
1 , где n=5,6,7,… (18)
42 n2 n4
Переходы для серий Лаймана и Бальмера приведены на рисунке 5.
Помимо прочего, формула (13) позволяет оценить энергию ионизации атома водорода:
E h
hc
hcR 1
1 hcR
(19)