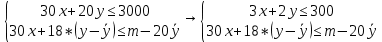Файл: 1министерство науки и высшего образования российской федерации.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| Институт финансов, экономики и управления |
| (Наименование учебного структурного подразделения) |
| 38.03.01 Экономика |
| (код и наименование направления подготовки / специальности) |
| Финансовый менеджмент |
| (направленность (профиль) / специализация) |
Практическое задание № 1
по учебному курсу «Микроэкономика»
(наименование учебного курса)
Вариант 5 (при наличии)
| Обучающегося | Алла Владимировна Морозова | |
| | (И.О. Фамилия) | |
| Группа | ЭКбвд-2206а | |
| | | |
| Преподаватель | Шерстнев Михаил Анатольевич | |
| | (И.О. Фамилия) | |
Тольятти 2023
| |
| |
Практическое задание 1
Вариант 5
Задача 1
Кривая индивидуального спроса на некоторое благо линейна и при цене P=10 эластичность спроса по цене εDp= -2. Достижение какого уровня цены P приведет к полному отказу от потребления этого товара?
Решение
1. Линейная функция спроса имеет вид:
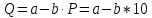
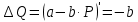
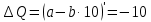
2. Коэффициент эластичности спроса по цене определяется по формуле:
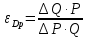
Подставим полученные значения и найдем, чем равен коэффициент а:
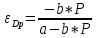
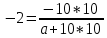
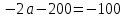
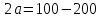
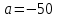
3. Найдем значение Р, при котором Q=0:
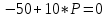
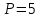
Ответ: уровень цены P=5 приведет к полному отказу от потребления товара.
Задача 2
Функция спроса на товар имеет вид
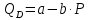. При каких значениях цены товара кривая спроса эластична? На графике покажите эластичный и неэластичные участки кривой спроса 
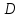.Решение:
1. Единичная эластичность спроса соответствует формуле:
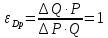
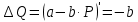
Следовательно:
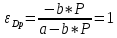
Спрос имеет единичную эластичность по цене в средней точке при:
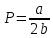
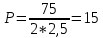
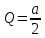
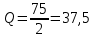
Спрос эластичен на участке:
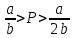
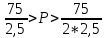
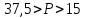
Спрос неэластичен на участке:
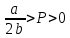
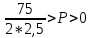
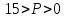
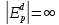
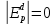
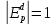
D
75
15
P
37,5
37,5
Q
Рисунок 1
Практическое задание 2
Вариант 5
Предположим, что доход потребителя в месяц составляет m=3000 руб. на потребительский набор (x, y). Цена единицы товара x равна Рx=30 руб., а цена единицы товара y равна Рy=20 руб.
1. Запишите бюджетное ограничение (БО) потребителя и покажите на графике соответствующее бюджетное множество (БМ).
2. Изменения в экономике привели к необходимости ввести налог на цену товара x. Теперь каждая единица товара x будет обходиться всем потребителям на τ=10% дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?
3. В результате введения правительством налога на цену товара администрацией региона была введена потоварная субсидия на товар y, равная сумме s=2 руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?
Решение:
1. Бюджетное ограничение по заданным значениям принимает вид:
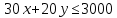
Представим бюджетное множество в графическом виде:
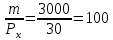
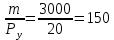
y
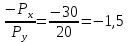
150
3000
-1,5
100
x
Рисунок 2.1
2. Введение налога на стоимость товара x привело к изменению цены Рx. Фактическая цена составила:
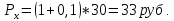
Бюджетное ограничение принимает вид:
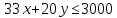
Бюджетные множества:
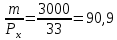
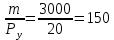
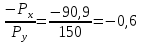
y
x
150
3000
-1,5
-0,6
100
90,9
Рисунок 2.3
Вывод: множество доступных потребителю наборов после ограничительной политики правительства уменьшилось.
3. Сохраняя условия п. 2, администрация региона ввела потоварную субсидию на товар y в размере 2 руб. Фактическая цена составила:
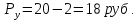
Бюджетное ограничение принимает вид:
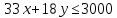
Бюджетные множества:
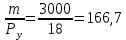
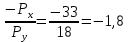
y
x
166,7
-1,8
150
3000
-0,6
100
90,9
Рис. 2.3
Вывод: множество доступных потребителю наборов после ограничительной политики правительства увеличилось.
4. Условия пунктов 2 и 3 отменены. Магазин ввел следующую систему скидок: при покупке товара y все приобретенные единицы продаются на S=2 руб. дешевле. Для нахождения бюджетного ограничения решаем систему уравнений:
