Файл: Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования по дисциплине Гидравлика и нефтегазовая гидромеханика.docx
Добавлен: 11.01.2024
Просмотров: 198
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство высшего образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего
образования
«Уфимский государственный нефтяной технический университет»
Кафедра «Гидрогазодинамика трубопроводных систем и гидромашины»
КУРСОВАЯ РАБОТА
«Гидравлический расчет сложного трубопровода и элементов оборудования»
по дисциплине «Гидравлика и нефтегазовая гидромеханика»
Выполнил: студент гр. БМТ-19-03 _____________ П.А. Багина
(подпись, дата)
Проверил: _____________ Л.Р. Байкова
(подпись, дата)
Уфа 2021
СОДЕРЖАНИЕ
1 Задача 2.18 5
Замкнутый резервуар с нефтью (ρ = 900 кг/м3) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а = 1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M = 15 кПа, а в правой - показанием вакуумметра V = 10 кПа. Уровни нефти указаны на эскизе. Найти величину Р и плечо х результирующей силы давления на крышку, закрывающую отверстие в перегородке. 5
5
Рисунок 1 – Схема к задаче 5
Решение: 5
Сила манометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо 5
. 5
Сила вакууметрического давления приложена там же и направлена справа налево 5
. 5
Сила гидростатического давления жидкости на плоскую стенку 5
, 5
где – расстояние от свободной поверхности до центра тяжести стенки площадью . 6
Точка приложения – центр давления 6
, 6
где – центральный момент инерции. 6
Сила давления слева 6
. 6
Расстояние от свободной поверхности до центра давления слева 6
. 6
Сила давления справа 6
. 6
Расстояние от свободной поверхности до центра давления справа 6
. 6
Суммарная сила 6
. 6
Рассмотрим схему сил и обозначим 6
, 6
. 6
. 6
7
Рисунок 2 – Схема действия сил 7
Ответ: . 7
2 Задача 3.1 8
Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D = 1 м в трех случаях: y = + D/5, y = - D/5, y = 0. 8
Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища. 8
8
Рисунок 3 – Схема к задаче 8
Решение 8
Площадь вертикальной проекции плоского и полусферического днища 8
м2. 8
Горизонтальная составляющая силы давления 8
, 8
где – избыточное давление в центре тяжести днища. 8
1) м; Па; Н; 8
2) м; Па; Н; 9
3) м; Па; Н. 9
9
9
Рисунок 4 – Схема действия сил 9
Вертикальная составляющая силы давления на полусферическую крышку во всех трех случаях одинакова, так как объем тела давления одинаков и равен 9
м3. 10
Вертикальная составляющая силы давления 10
, 10
Н. 10
Суммарная сила давления: 10
1) Н кН, 10
, ; 10
2) Н кН, 10
, ; 10
3) Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы. 10
3 Гидравлический расчет разветвленного трубопровода 10
Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается. Определить Pвх, Q1 = Q2, Q3, Q4. 11
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 24
1 Задача 2.18
Замкнутый резервуар с нефтью (ρ = 900 кг/м3) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а = 1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M = 15 кПа, а в правой - показанием вакуумметра V = 10 кПа. Уровни нефти указаны на эскизе. Найти величину Р и плечо х результирующей силы давления на крышку, закрывающую отверстие в перегородке.
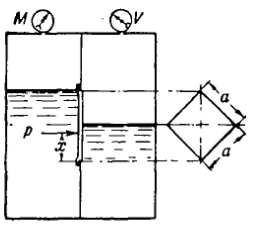
Рисунок 1 – Схема к задаче
Решение:
Сила манометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо
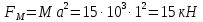 .
.Сила вакууметрического давления приложена там же и направлена справа налево
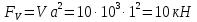 .
.Сила гидростатического давления жидкости на плоскую стенку
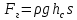 ,
,где
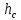 – расстояние от свободной поверхности до центра тяжести стенки площадью
– расстояние от свободной поверхности до центра тяжести стенки площадью 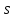 .
.Точка приложения
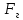 – центр давления
– центр давления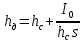 ,
,где
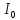 – центральный момент инерции.
– центральный момент инерции.Сила давления слева
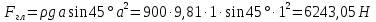 .
.Расстояние от свободной поверхности до центра давления слева
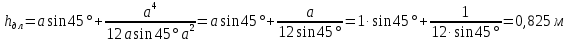 .
.Сила давления справа
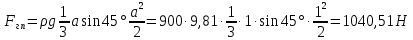 .
.Расстояние от свободной поверхности до центра давления справа
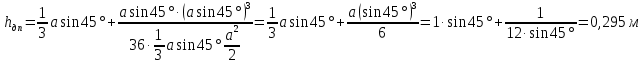 .
.Суммарная сила
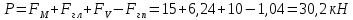 .
.Рассмотрим схему сил и обозначим
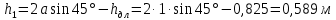
,
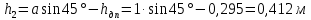 .
.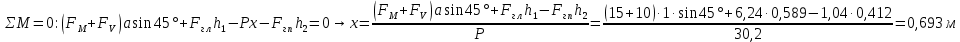 .
.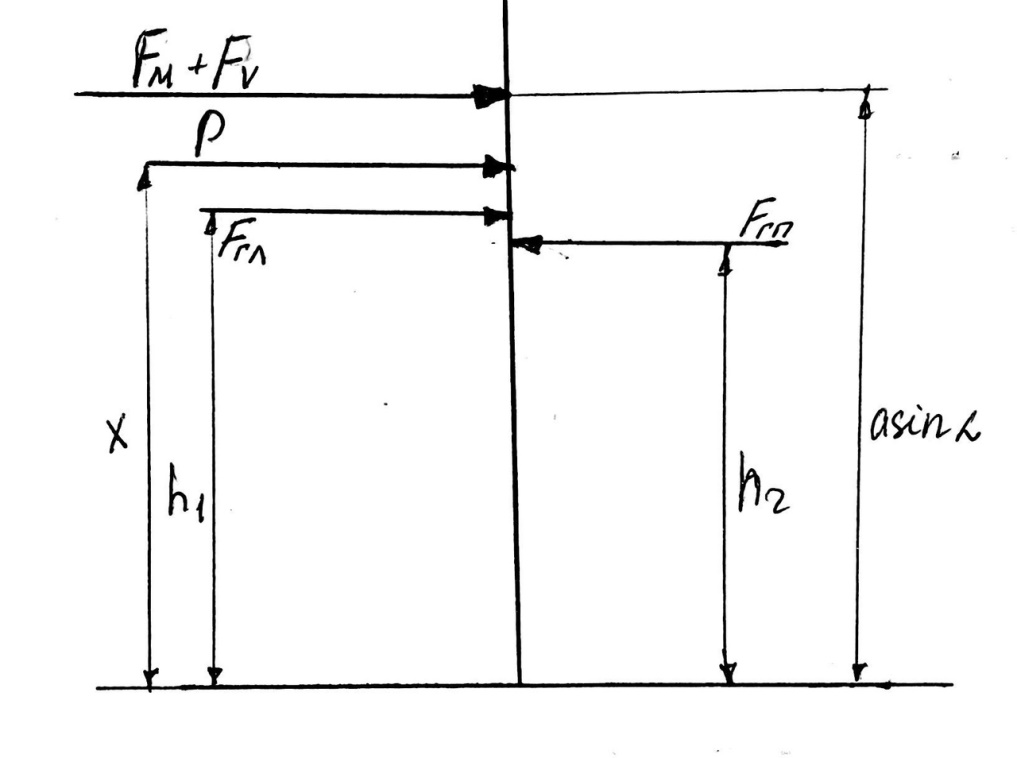
Рисунок 2 – Схема действия сил
Ответ:
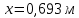 .
.2 Задача 3.1
Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D = 1 м в трех случаях: y = + D/5, y = - D/5, y = 0.
Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища.
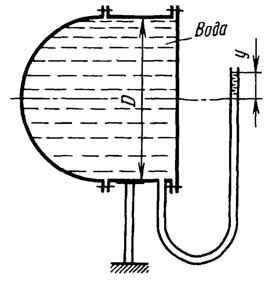
Рисунок 3 – Схема к задаче
Решение
Площадь вертикальной проекции плоского и полусферического днища
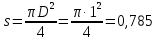 м2.
м2.Горизонтальная составляющая силы давления
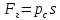 ,
,где
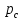 – избыточное давление в центре тяжести днища.
– избыточное давление в центре тяжести днища.1)
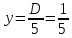 м;
м; 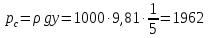 Па;
Па; 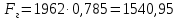 Н;
Н;2)
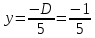 м;
м; 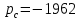 Па;
Па; 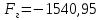 Н;
Н;3)
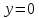 м;
м; 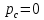 Па;
Па; 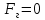 Н.
Н.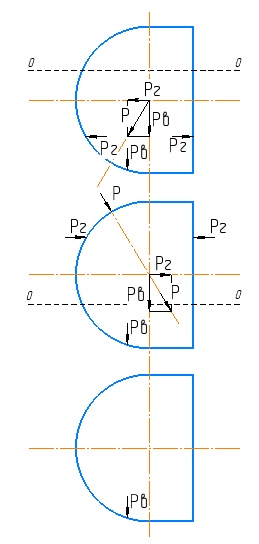
Рисунок 4 – Схема действия сил
Вертикальная составляющая силы давления на полусферическую крышку во всех трех случаях одинакова, так как объем тела давления одинаков и равен
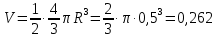 м3.
м3.Вертикальная составляющая силы давления
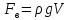 ,
,
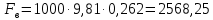 Н.
Н.Суммарная сила давления:
1)
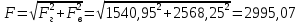 Н
Н 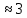 кН,
кН,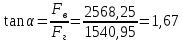 ,
, 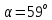 ;
;2)
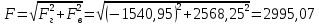 Н
Н 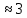 кН,
кН,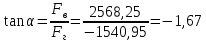 ,
, 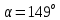 ;
;3)
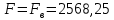 Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы.
Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы.3 Гидравлический расчет разветвленного трубопровода
Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается. Определить Pвх, Q1 = Q2, Q3, Q4.
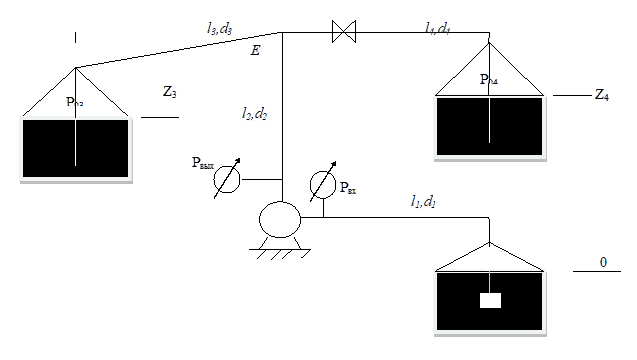
Рисунок 5 – Схема разветвленного трубопровода
Исходные данные:
Проектный расход, м3/ч _____________
Перекачиваемая жидкость ρ = 900 кг/м3; ν = 30⋅10-6 м2/c
Температура перекачки __________________________
Эквивалентная шероховатость_Кэ = 0,2 мм___________
| № | l, м | d, мм | zн, м | zк, м | Pн, кПа | Pк, кПа | Q, м3/ч | Примечание |
| 1 | 50 | 100 | z1 = 0 | zвх = 2 | P01 = Pат | Pвх - ? | | 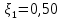 |
| 2 | 200 | 100 | zвых = 2 | zЕ | Pвых = 800 | PЕ | | 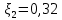 |
| 3 | 150 | 60 | zЕ | z3 = 6 | PЕ | P03 = 100 | | 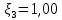 |
| 4 | 130 | 80 | zЕ | z4 = 6 | PЕ | P04 = 100 | | 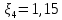 |
3.1. Теоретическая часть.
Для решения сформулированных выше задач составляется система уравнений, устанавливающая связи между размерами труб, расходами жидкости, напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравнений Бернулли для каждой ветви трубопровода. При этом в сложных трубопроводах можно пренебрегать относительно малыми местными потерями напора в узлах. Это позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и оперировать в уравнениях Бернулли понятием напора в данном узле.
Уравнение Бернулли для участка трубопровода 1-2 записывается в виде
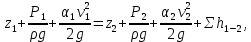 (1)
(1)где z – геометрический напор, м;
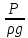 – пьезометрический напор, м;
– пьезометрический напор, м;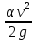 – скоростной напор, м;
– скоростной напор, м;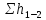 – потери напора, м.
– потери напора, м.В данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому
Потери напора в трубах выражаются формулой Дарси–Вейсбаха (см.[2] стр. 103):
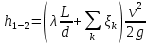 , (2)
, (2)где L – длина трубы;
d – диаметр трубы;
λ – коэффициент сопротивления трения;
ξ – коэффициент местного сопротивления;
υ – средняя скорость потока в трубе.
Поскольку средняя скорость потока в трубе выражается формулой
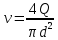 , (3)
, (3)где Q – расход жидкости в трубе;
то потери напора можно написать в следующем виде
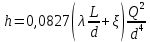 . (4)
. (4)Коэффициент гидравлического сопротивления λ зависит от режима течения жидкости и является функцией расхода