Файл: Умноженной на множитель в форме показательной функции W.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 445
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
дополненных нулями последовательностей, соответствует расчету линейной свертки исходных сигналов. Чтобы убедиться в этом, достаточно использовать матричную запись циклической свертки, и расписать соответствующие элементы  ,
, 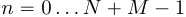 . В результате выражения
. В результате выражения  будут соответствовать линейной свертке.
будут соответствовать линейной свертке.
Необходимо заметить, что добивать и
и  нулями можно не только до длины
нулями можно не только до длины  , но и до любой длины
, но и до любой длины 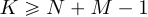 . В результате вычисления циклической свертки дополненных нулями последовательностей до длины , первый
. В результате вычисления циклической свертки дополненных нулями последовательностей до длины , первый  значение на выходе будет представлять собой линейную свертку, а остальные значения будут нулевыми. Это можно использовать для дополнения исходных последовательностей нулями до длины, которая допускает использование эффективных БПФ алгоритмов.
значение на выходе будет представлять собой линейную свертку, а остальные значения будут нулевыми. Это можно использовать для дополнения исходных последовательностей нулями до длины, которая допускает использование эффективных БПФ алгоритмов.
Например при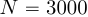 и
и 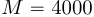 , необходимо дополнить
, необходимо дополнить  и
и  нулями до длины
нулями до длины 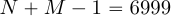 . Однако мы можем дополнить их до длины
. Однако мы можем дополнить их до длины 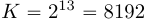
отсчетов и использовать БПФ по основанию два для расчета циклической свертки. При этом первые 6999 отсчетов результата циклической свертки будут представлять собой линейную свертку при и
и  . Использование алгоритма БПФ для
. Использование алгоритма БПФ для 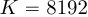 приведет к десятикратному снижению требуемых вещественных умножителей при вычислении линейной свертки при
приведет к десятикратному снижению требуемых вещественных умножителей при вычислении линейной свертки при  и
и  .
.
Проектирование ЦФ выполняется в три этапа:
Двум типам ЛДС – КИХ и БИХ – соответствуют два типа ЦФ:
Для ЧИФ (ФНЧ, ФВЧ, ПФ, РФ) в виде требований предъявляют:
Метод синтеза зависит от типа ЦФ (КИХ или БИХ), а в рамках одного типа – от специфики дополнительных требований (простоты метода, оптимальности проектируемого фильтра и др.).
Структура ЦФ может быть реализована на базе цифрового устройства – цифрового процессора обработки сигналов (ЦПОС), программируемой логической интегральной схеме (ПЛИС) и т. п.
Физический смысл свойства
линейности ФЧХ – постоянная групповая задержка фильтра.
Групповая задержка – время задержки реакции фильтра относительно воздействия. В общем случае (при нелинейной ФЧХ) при разных частотах сигнала воздействия, время задержки разное и зависит от частоты входного воздействия.
Пример.
Пусть на фильтр оказали гармоническое воздействие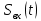 с частотой
с частотой 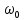 и получили реакцию
и получили реакцию 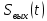 . При этом между входным и выходным сигналами наблюдается разница фаз, равная
. При этом между входным и выходным сигналами наблюдается разница фаз, равная 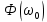 , которой соответствует величина задержки по времени
, которой соответствует величина задержки по времени
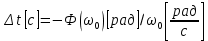 .
.
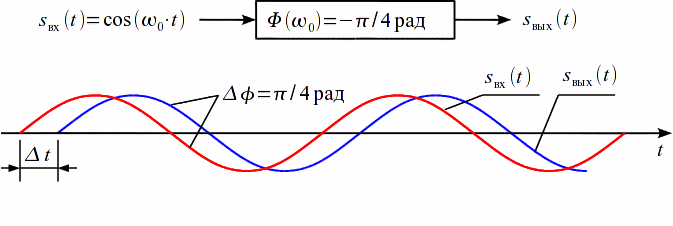
Рис. 19.1 – Пример гармонического воздействия и реакции фильтра (с задержкой)
В общем случае время задержки определяется следующим образом:
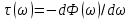
В случае линейной ФЧХ время задержки для всех частот одинаковое, т.к. производная линейной функции есть константа: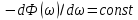 . Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать.
. Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать.
Если же сигнал проходит через фильтр с нелинейной ФЧХ, какие-то гармоники воздействия будут приходить на выход быстрее, чем другие, что приведёт к искажениям формы сигнала.
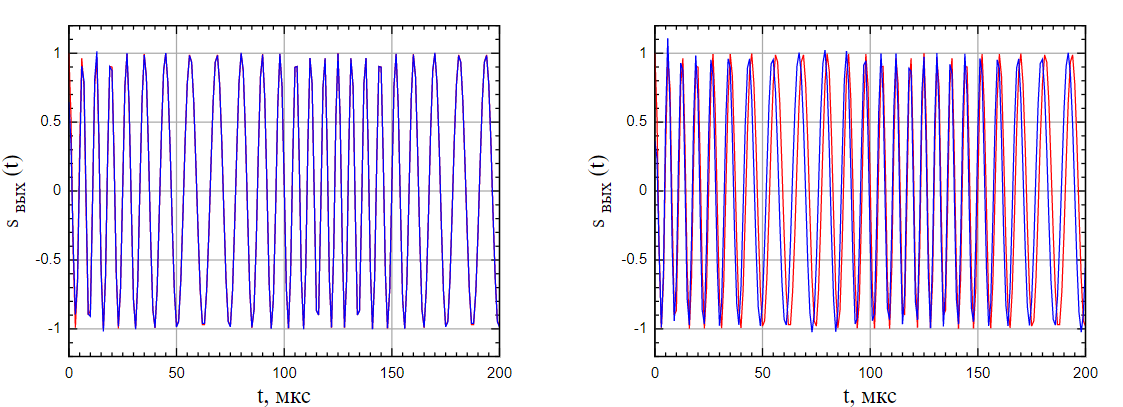
Рис. 19.2 – Демонстрация разницы ГВЗ при линейной (слева) и нелинейной (справа) ФЧХ
Условием линейной ФЧХ КИХ-фильтра является симметрия\антисимметрия его ИХ.
Доказательство.
Пусть линейная ФЧХ будет иметь следующий вид: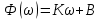 .
.
Для дальнейшего доказательства напомним, что комплексная передаточная функция и импульсная характеристика фильтра связаны между собой преобразованием Фурье:
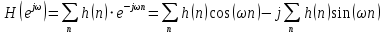
Запишем ФЧХ через комплексную передаточную функцию фильтра и составим уравнение:
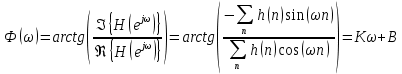
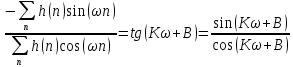
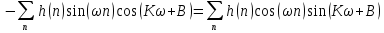
По формуле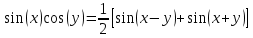 :
:
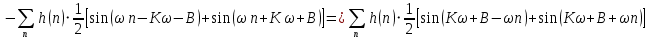
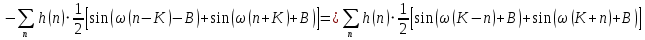
Внесём знак «-» внутрь суммы синусов левой части уравнения и преобразуем:
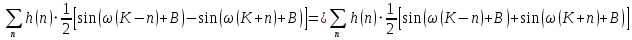
Перенесём правую часть в левую и сократим подобные:
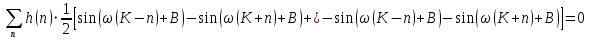
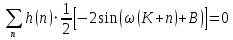
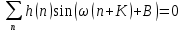
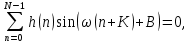
где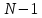 – порядок КИХ-фильтра.
– порядок КИХ-фильтра.
Получили условие линейной ФЧХ. Рассмотрим 2 частных, самых очевидных случая, когда оно будет выполняться. Эти случаи базируются на понятиях симметричной\антисимметричной ИХ, хотя ЛФЧХ можно достичь и при нарушении симметрии ИХ, однако здесь это не описывается.
Уравнение будет выполняться если множители под суммой (отсчёты ИХ и гармонический сигнал) будут обладать свойством чётности\нечётности относительно центра ИХ, причём поочерёдно:
Для получения синуса коэффициент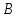 должен быть кратен
должен быть кратен 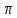 , а коэффициент
, а коэффициент 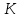 должен центрировать синус к центру ИХ КИХ-фильтра, то есть
должен центрировать синус к центру ИХ КИХ-фильтра, то есть 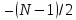 .
.
При таких коэффициентах уравнение примет вид:
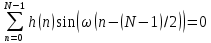
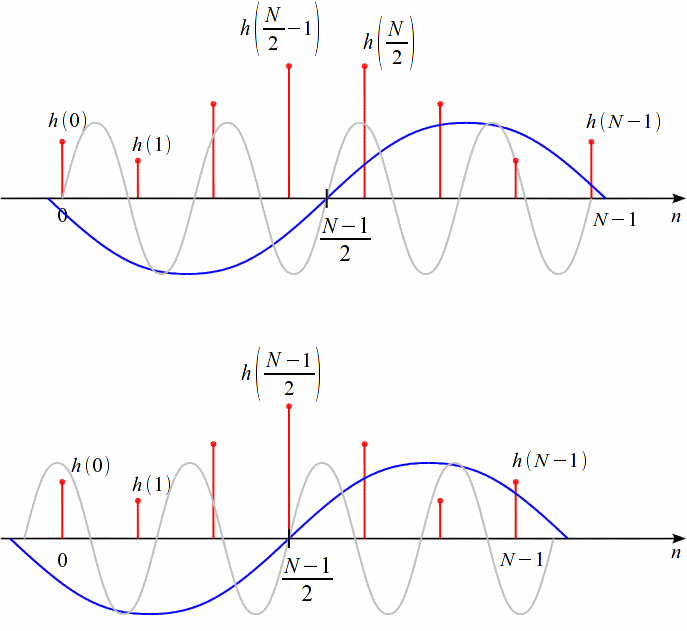
Рис. 19.3 – Примеры симметричной ИХ при чётном и нечётном порядках фильтра
Для обеспечения чётности гармонического сигнала коэффициент должен быть равен
должен быть равен 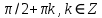 . При таких коэффициентах уравнение примет вид:
. При таких коэффициентах уравнение примет вид:
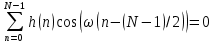
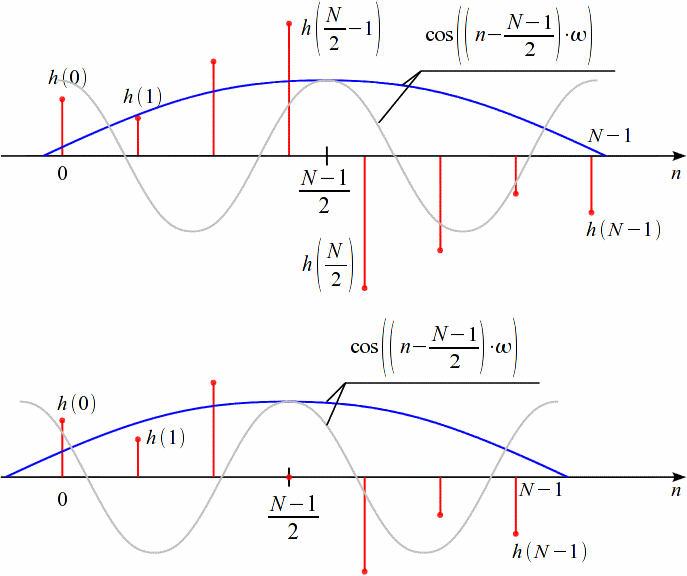
Рис. 19.4 – Примеры антисимметричной ИХ при нечётном и чётном порядках фильтра
Необходимо заметить, что добивать
Например при
отсчетов и использовать БПФ по основанию два для расчета циклической свертки. При этом первые 6999 отсчетов результата циклической свертки будут представлять собой линейную свертку при
- Этапы проектирования цифровых фильтров. Требования к АЧХ, предъявляемые при синтезе фильтров. КИХ-фильтры с линейной ФЧХ, свойства. Порядок фильтра и длина импульсной характеристики. Проектирование КИХ-фильтров методом окон. Эффект Гиббса и назначение окон (на примере окна Кайзера). Структуры КИХ-фильтров с симметричной и антисимметричной импульсной характеристикой.
Проектирование ЦФ выполняется в три этапа:
-
Синтез ЦФ. Включает следующие основные шаги:-
Выбор типа ЦФ
-
Двум типам ЛДС – КИХ и БИХ – соответствуют два типа ЦФ:
-
КИХ-фильтр (FIR Filter – Finite Impulse Response Filter); -
БИХ-фильтр (HR Filter – Infinite Impulse Response Filter).
-
Задание требований к характеристикам ЦФ
Для ЧИФ (ФНЧ, ФВЧ, ПФ, РФ) в виде требований предъявляют:
-
Частота дискретизации; -
Граничные частоты полос пропускания\затухания; -
Минимальный уровень ослабления в ПЗ; -
Допустимые уровни пульсации АЧХ в ПП и ПЗ; -
Линейность ФЧХ.
-
Выбор метода синтеза
Метод синтеза зависит от типа ЦФ (КИХ или БИХ), а в рамках одного типа – от специфики дополнительных требований (простоты метода, оптимальности проектируемого фильтра и др.).
-
Расчёт передаточной функции ЦФ -
Выбор структуры ЦФ
-
Моделирование структуры ЦФ с учётом эффектов квантования -
Реализация структуры ЦФ
Структура ЦФ может быть реализована на базе цифрового устройства – цифрового процессора обработки сигналов (ЦПОС), программируемой логической интегральной схеме (ПЛИС) и т. п.
Физический смысл свойства
линейности ФЧХ – постоянная групповая задержка фильтра.
Групповая задержка – время задержки реакции фильтра относительно воздействия. В общем случае (при нелинейной ФЧХ) при разных частотах сигнала воздействия, время задержки разное и зависит от частоты входного воздействия.
Пример.
Пусть на фильтр оказали гармоническое воздействие
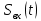 с частотой
с частотой 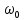 и получили реакцию
и получили реакцию 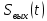 . При этом между входным и выходным сигналами наблюдается разница фаз, равная
. При этом между входным и выходным сигналами наблюдается разница фаз, равная 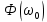 , которой соответствует величина задержки по времени
, которой соответствует величина задержки по времени 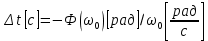 .
.
Рис. 19.1 – Пример гармонического воздействия и реакции фильтра (с задержкой)
В общем случае время задержки определяется следующим образом:
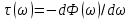
В случае линейной ФЧХ время задержки для всех частот одинаковое, т.к. производная линейной функции есть константа:
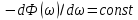 . Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать.
. Так как все гармоники воздействия будут приходить на выход с одинаковой задержкой, форма сигнала не исказится, а время задержки можно будет скомпенсировать.Если же сигнал проходит через фильтр с нелинейной ФЧХ, какие-то гармоники воздействия будут приходить на выход быстрее, чем другие, что приведёт к искажениям формы сигнала.

Рис. 19.2 – Демонстрация разницы ГВЗ при линейной (слева) и нелинейной (справа) ФЧХ
Условием линейной ФЧХ КИХ-фильтра является симметрия\антисимметрия его ИХ.
Доказательство.
Пусть линейная ФЧХ будет иметь следующий вид:
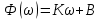 .
.Для дальнейшего доказательства напомним, что комплексная передаточная функция и импульсная характеристика фильтра связаны между собой преобразованием Фурье:
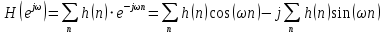
Запишем ФЧХ через комплексную передаточную функцию фильтра и составим уравнение:
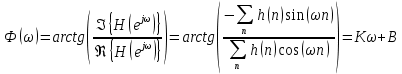
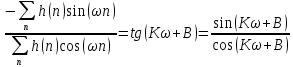
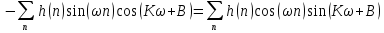
По формуле
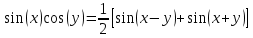 :
: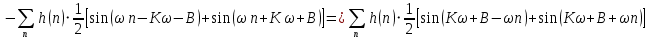
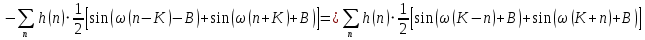
Внесём знак «-» внутрь суммы синусов левой части уравнения и преобразуем:
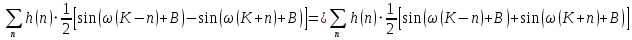
Перенесём правую часть в левую и сократим подобные:
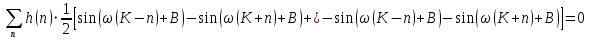
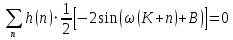
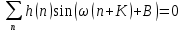
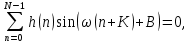
где
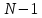 – порядок КИХ-фильтра.
– порядок КИХ-фильтра.Получили условие линейной ФЧХ. Рассмотрим 2 частных, самых очевидных случая, когда оно будет выполняться. Эти случаи базируются на понятиях симметричной\антисимметричной ИХ, хотя ЛФЧХ можно достичь и при нарушении симметрии ИХ, однако здесь это не описывается.
Уравнение будет выполняться если множители под суммой (отсчёты ИХ и гармонический сигнал) будут обладать свойством чётности\нечётности относительно центра ИХ, причём поочерёдно:
-
ИХ чётна, гармонический сигнал нечётен (синус)
Для получения синуса коэффициент
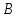 должен быть кратен
должен быть кратен 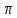 , а коэффициент
, а коэффициент 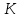 должен центрировать синус к центру ИХ КИХ-фильтра, то есть
должен центрировать синус к центру ИХ КИХ-фильтра, то есть 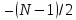 .
.При таких коэффициентах уравнение примет вид:
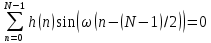

Рис. 19.3 – Примеры симметричной ИХ при чётном и нечётном порядках фильтра
-
ИХ нечётна, гармонический сигнал чётен (косинус)
Для обеспечения чётности гармонического сигнала коэффициент
 должен быть равен
должен быть равен 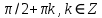 . При таких коэффициентах уравнение примет вид:
. При таких коэффициентах уравнение примет вид: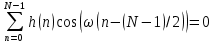

Рис. 19.4 – Примеры антисимметричной ИХ при нечётном и чётном порядках фильтра