Файл: Умноженной на множитель в форме показательной функции W.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 441
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( δ – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.
Выберем в качестве элементарного сигнала δ – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом
Очевидно, выходной сигнал
Так как оператор Wц не зависит от времени, его можно внести под знак интеграла. Тогда
Если момент появления входного сигнала t0=0, то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид
Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента t0=0 и заканчивая текущим моментом времени t. Роль весовой функции выполняет импульсная характеристика цепи.
- 1 2 3 4 5 6 7 8
Понятие о циклической (круговой) свертке. Связь круговой свертки и ДПФ. Использование циклической свертки для вычисления линейной свертки. Быстрая свертка через БПФ. Примеры.
Понятие о циклической свертке:
Пусть имеется две последовательности
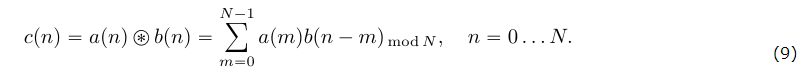
Как можно видеть из (9) циклическую свертку можно выполнять только над последовательностями равной длины отсчетов, причем результатом также будет последовательность длины .
Графически пример вычисления циклической свертки (9) для

Рисунок 5. Пример вычисления циклической свертки
Заметим, что вычисление циклической свертки можно представить в матричной форме:
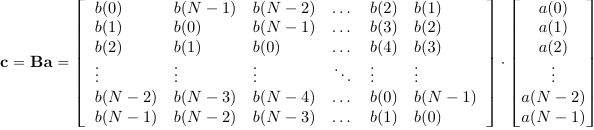
(10)
Можно видеть, что каждый столбец матрицы циклически задержан на один отсчет относительно предыдущего столбца. Особая структура матрицы допускает разработку высокоэффективных алгоритмов расчета циклической свертки [2].
Про связь Циклической свертки и ДПФ (немного) и Алгоритм быстрого вычисления циклической свертки на основе БПФ:
Важнейшим свойством циклической свертки является то, что она
сводится к произведению спектров ДПФ исходных последовательностей, а также к произведению их -образов. Использование аппарата быстрого преобразования Фурье обеспечивает высочайшую вычислительную эффективность циклических сверток.
Как мы знаем из свойств дискретного преобразования Фурье, ДПФ циклической свертки равно произведению спектров сворачиваемых сигналов:
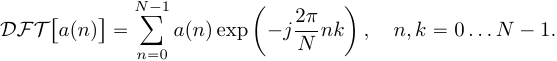 (12)
(12)Таким образом перемножив поэлементно спектры ДПФ исходных сигналов, и в взяв обратное дискретное преобразование Фурье, мы получим результат циклической свертки
где
Схематично процесс расчета циклической свертки сигналов и использованием алгоритмов быстрого преобразования Фурье показан на рисунке 6.
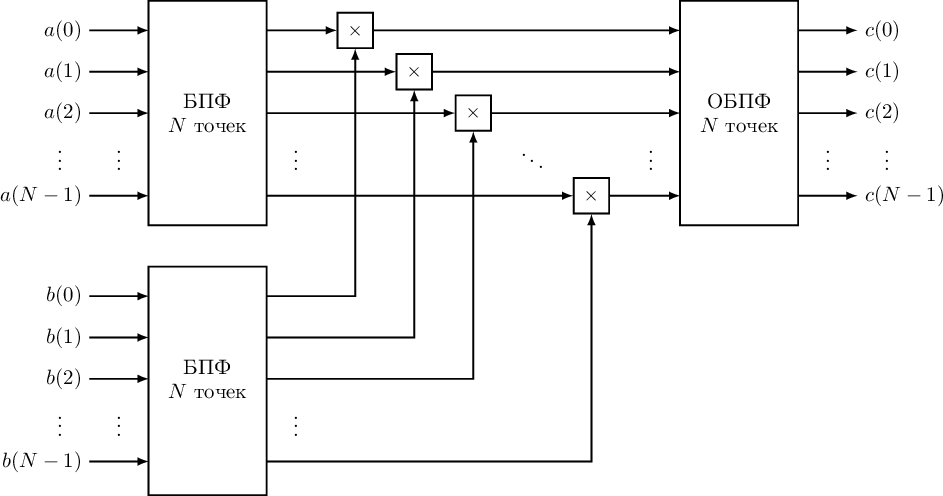
Рисунок 6. Вычисление циклической свертки на основе БПФ
Заметим, что эффективность алгоритмов БПФ зависит от длины выборки . Наиболее эффективные алгоритмы разработаны для длины равной целой степени двойки (так называемые алгоритмы по основанию два). При этом помимо высокой вычислительной эффективности, алгоритмы БПФ по основанию два отличаются регулярными структурами при аппаратной и программной реализации, а также прекрасно распараллеливаются при мультипроцессорной обработке.
Например для
Каждое из трех БПФ требует количество умножений равное:
(14)
тогда получаем, что расчет свертки через БПФ требует
Использование циклической свертки для вычисления линейной свертки.
Вычислительные преимущества, которые мы получаем при использовании аппарата БПФ для расчета циклической свертки, хотелось бы также получать и для расчета линейной свертки. С этой целью рассмотрим способ приведения линейной свертки последовательностей ограниченной длительности к циклической.
Пусть
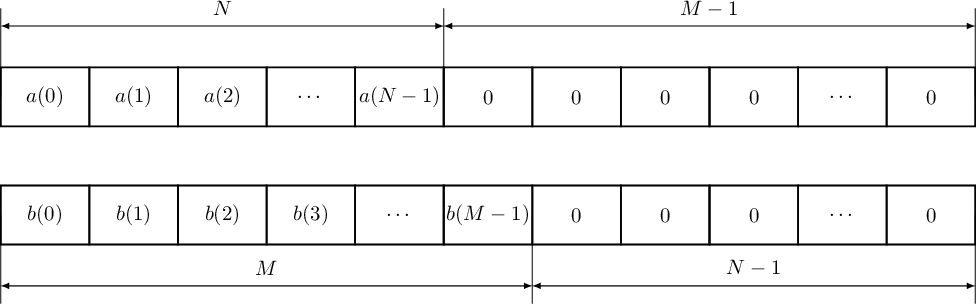
Рисунок 7. Добавление нулей для приведения линейной свертки к циклической
К последовательности
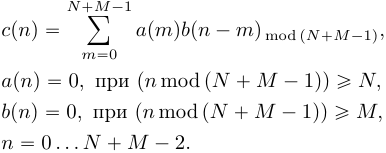
(15)
Можно показать, что циклическая свертка (15)