Файл: Умноженной на множитель в форме показательной функции W.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 443
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
, получим комплексный коэффициент передачи АФП 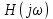 . При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра.
. При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра.
Поскольку нули и полюса обладают квадратной симметрией, то мы всегда будем иметь дело с комплексно-сопряжёнными парами нулей и полюсов и для фильтра второго порядка получим:
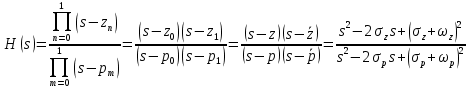
Данное представление называют биквадратной формой (биквадратный фильтр). Фильтр любого чётного порядка может быть представлен при помощи биквадратных форм. Таким образом достаточно рассчитать только половину нулей и полюсов фильтра, а вторая половина будет комплексно-сопряжённой.
Билинейное Z-преобразование основано на замене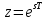 . Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ).
. Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ).
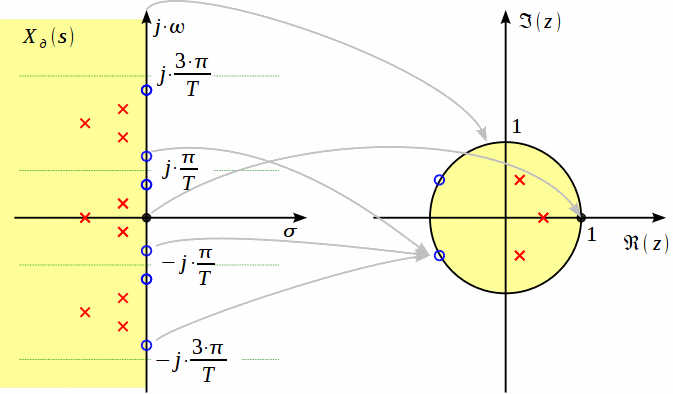
Рис. 20.1 – Графическое отображение s-плоскости в z-плоскость
Если имеется передаточная функция АФП , можно получить передаточную функцию цифрового фильтра:
, можно получить передаточную функцию цифрового фильтра:
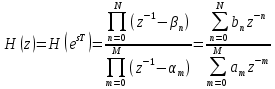
где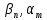 – отображённые на z-плоскость нули и полюса соответственно,
– отображённые на z-плоскость нули и полюса соответственно,
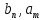 – коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых.
– коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых.
Однако подстановку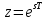 не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограни
не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограни
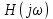 . При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра.
. При этом модуль этого коэффициента будет являться АЧХ фильтра, а аргумент – ФЧХ фильтра.Поскольку нули и полюса обладают квадратной симметрией, то мы всегда будем иметь дело с комплексно-сопряжёнными парами нулей и полюсов и для фильтра второго порядка получим:
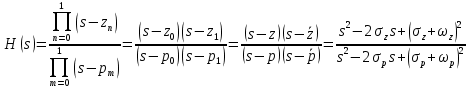
Данное представление называют биквадратной формой (биквадратный фильтр). Фильтр любого чётного порядка может быть представлен при помощи биквадратных форм. Таким образом достаточно рассчитать только половину нулей и полюсов фильтра, а вторая половина будет комплексно-сопряжённой.
-
Преобразование передаточной функции АФП в передаточную функцию БИХ-фильтра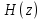 на основе формулы билинейного Z-преобразования
на основе формулы билинейного Z-преобразования
Билинейное Z-преобразование основано на замене
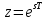 . Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ).
. Данная подстановка позволяет отобразить комплексную s-плоскость АФП в z-плоскость цифрового фильтра. При этом левая полуплоскость s-плоскости (область устойчивости полюсов АФП) отобразится в единичный круг z-плоскости (область устойчивости полюсов ЦФ).
Рис. 20.1 – Графическое отображение s-плоскости в z-плоскость
Если имеется передаточная функция АФП
 , можно получить передаточную функцию цифрового фильтра:
, можно получить передаточную функцию цифрового фильтра: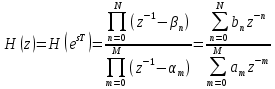
где
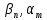 – отображённые на z-плоскость нули и полюса соответственно,
– отображённые на z-плоскость нули и полюса соответственно,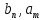 – коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых.
– коэффициенты передаточной функции ЦФ, полученные путём раскрытия произведений нулей и полюсов и приведения подобных слагаемых.Однако подстановку
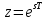 не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограни
не всегда удобно использовать и вместо неё используют дробно-рациональную подстановку, которая получается из исходной замены при помощи разложения экспоненты в ряд Тейлора с последующим ограни