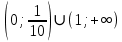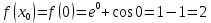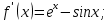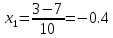
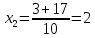
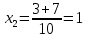
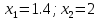
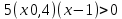
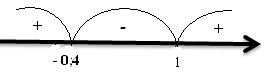
Анықталу облысы:

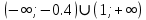
х – тің екі мән 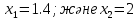анықталу облысына енеді, сондықтан -1;4 және 2 теңдеудің жауабы болады.

Жауабы: -1,4; 2

3. 
   Берілген функциялардың графиктерімен шектелген фигураның ауданын табыңдар.
   

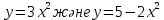
Шешуі:

Берілген функциялардың графиктерін бір координата жазықтығына наубайын сызамыз.

1)

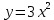
2)



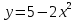
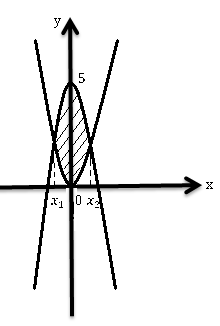
Графиктердің қиылысу нүктелерінің

абсциссасын табу үшін, функцияларды

теңестіреміз, яғни,







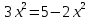
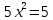
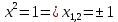
Бұдан 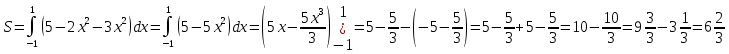Жауабы: 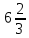кв бар.

4. 
   Функцияның графигіне абсциссасы х₀=1 нүктесінде жүргізілген жанаманың теңдеуін жазыңдар.
   

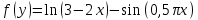
Шешуі:

Жанаманың теңдеуі:







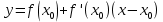
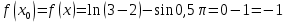
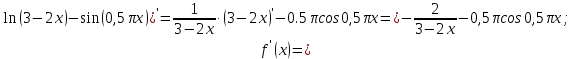
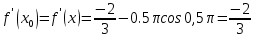
Онда,

---

5. 
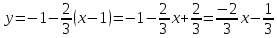
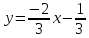
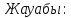
   Теңсіздікті шешіңдер:
   

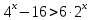
Шешуі:



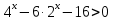
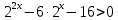жаңа айнымалы енгіземіз.

Онда:



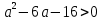
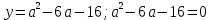
Виет теоремасы бойынша:



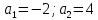
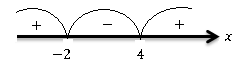
яғни,









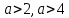
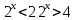
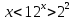
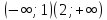
Жауабы:

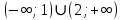
Мектеп курсына математика пәнінен бітіру емтиханына келетін

мүмкін есептер

ІІ нұсқа

1. 
   Теңдеуді шешіңдер:
   

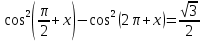
Шешуі:

Келтіру формуласы бойынша















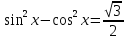
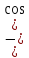
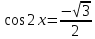
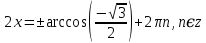
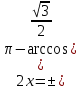
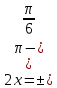
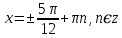
Жауабы:

2. 
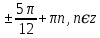
   Теңдеуді шешіңдер
   

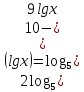
Шешуі:

---

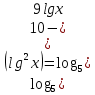
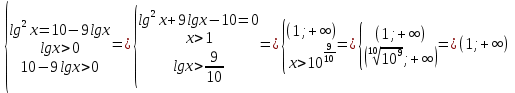
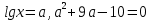
Виет теоремасы бойынша

1. 
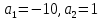
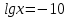   2)
   

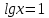
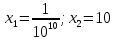
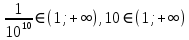
Жауабы:10

3. 
   Берілген функциялардың графиктерімен шектелген фигураның ауданын табыңдар.
   

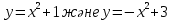
Шешуі:

Б 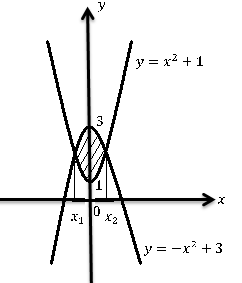ерілген функциялардың графиктерін наубайын бір координата жазықтығында сызамыз.

1)

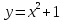
2)

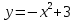
Графиктердің қиылысу нүктелерінің

Абсциссасын анықтаймыз.







-

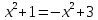
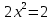
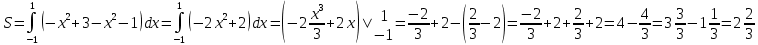Жауабы.

4. 
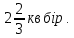
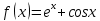   функциясының графигіне абсциссасы х₀=0 нүктеде жүргізілген жанаманың теңдеуін жазыңдар
   

Шешуі:

Жанаманың теңдеуі:

1. 
   
   
2. 
   
   

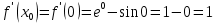
Сонда

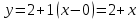
Жауабы:

5. 
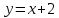
   Теңсіздікті шешіңдер:
   

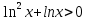
Шешуі:

Жаңа айнымалы енгіземіз.

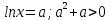теңсіздікті интервалдар әдісімен шешсек: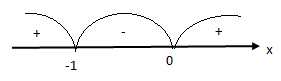

---

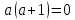
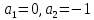
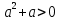теңсіздігінің шешімі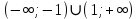

Онда

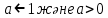
Сондықтан 1)



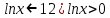
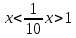
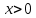екенін ескерсек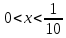



Жауабы:

---

Смотрите также файлы

• Практическая работа 5 Обоснование выбора средств проектирования информационной системы.docx

• Закон Ома для участка цепи Сопротивления провода.docx

• Кгбпоу бийский педагогический колледж.docx

• Методические рекомендации для проведения физических упражнений для студентов длительностью 2 мезоцикла.docx

• Блім 9блім. Мгілік елмгілік мрат.docx