Файл: Автоматтандыру адамды технологиялы рдістерді басару міндеттерін тікелей орындаудан босатып, бл міндеттерді автоматты рылылара артумен сипаттайтын кешенді механикаландыру кезеі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 405
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(10.30)
Түзусызықсыз жүйенің өзіндік ерекшелігі болып автотербеліс режимі табылады. Автотербелістер түзусызықсыз жүйелерге орнықты жұмыс режимі болады. Мысалы, түзусызықсыз басқарушы құрылғысы бар температураны автоматты түрде тұрақтандыру жүйесі. Түзусызықсыз жүйелерді талдағанда мынадай міндеттер шешіледі:
− жүйенің мүмкін болатын тепе-теңдік қалыптарын іздестіру және олардың орнықтылығын бағалау;
− автотербеліс параметрлерін және олардың жүйенің параметрлерімен байланысын анықтау.
Әдетте, түзусызықсыз жүйеде бір елеулі түзусызықсыз элемент болады.
Сызықты бөлім өзіне барлық сызықты немесе сызықтандырылған сипаттамалы элементтерді жинастырады және кез келген күрделі құрылымда бола алады.
Қарастырылып отырған жүйеде түзусызықсыз элементіміз температураның екіпозициялық реттеуіші, ал сызықты бөлім реттеуіш органнан (РО), басқару нысанынан (БО) және қабылдаушы органнан (ҚО) құралады.
Жүйенің орнықтылығын талдау
Автоматты басқару жүйесінің ең бір маңызды сипаттамасы, оның орнықтылығы. Орнықсыз жүйе жұмысқа жарамсыз, яғни ол басқару қызметтерін орындауға қабілетсіз және басқарылатын нысанды апаттық жағдайда алып келуі мүмкін. Кез келген практикалық жүйе орнықты болуы керек.
Нақты автоматты басқару жүйелерінің орнықтылық шарттарын А.М.Ляпунов тұжырымдады:
Осыған байланысты, беріліс функциясы төмендегідей жүйенің, сызықты бөлімінің орнықтылығына көз жеткізу керек.
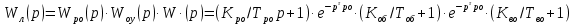(10.31)
Таза кешігуі бар екі буынды біріктіргенде алатынымыз:
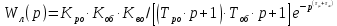(10.32)
Басқару жүйесінің контурында кешігу буыны болғанда жүйенің сипаттамалық теңдеуі трансценденттік болады, ал оларды шешу үлкен қиындықтар тудырады. Сондықтан практикалық есептерде трансценденттік беріліс функцияларын Пад қатарына жіктейді. Қатардың екі немесе үш мүшелерін ғана есепке алып, беріліс функциясын шамалап бөлшек рационал функциямен алмастырады
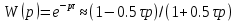(10.33)
мұндай ауыстыру қанағаттанарлық жуықтау береді, тек егер кірістегі сигналдың жиілігі
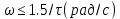(10.34)
Кешігу буынын жуықтап апроксимациялаудың басқа тәсілі, оны уақыт тұрақтылары бірдей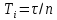
бірнеше бірінші ретті инерциялық буындардың тізбектей жалғануы түрінде көрсету.
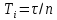(10.35)
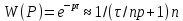(10.36)
Қарастырылып отырған жүйеге жоғары дәлдікті аппроксимация керексіздігін ескеріп, кешігу буынын беріліс функциясы төмендегідей бір ғана инерциялық буынмен алмастырамыз:
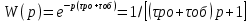(10.37)
Тиісінше жүйенің сызықты бөлімінің беріліс функциясының өрнегі:
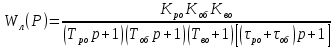(10.38)
қосындыны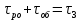
, белгілейміз.
Сызықты бөлімнің беріліс функциясын стандарттық формада жазамыз:
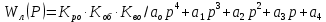(10.39)
мұндағы
;
; 
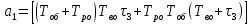
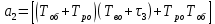
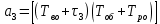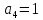
Гурвиц немесе Раус критерийлерін пайдаланып, сызықты жүйенің орнықтылығын анықтаймыз. Есептейлерді нақты жүйенің орнықтылығын анықтаған мысалда қарастырамыз. Жүйенің сызықты бөлімі орнықты болған жағдайда тұтас жүйенің орнықтылығын анықтауға көшеміз.
Түзусызықсыз жүйелердің орнықтылығын анықтау үшін (басқа әдістермен қатар) гармоникалық сызықтандыру (линериализация) әдісі қолданылады.
Гормоникалық сызықтандыру әдісі жуықтау әдіс, ол автотербелістерді туындау жағдайын және параметрлерді анықтауға мүмкіндік береді.
Жүйенің сипаттамалық полиномының реті жоғары болғанда, бұл әдіс едәуір есептеулерді талап етеді. Ал егер жүйенің сызықты бөлімін, яғни реттеулеріне қарасты өздігінен теңесетін біріккен статистикалық нысан болатын бөлімді, тізбектей қосылған бірінші ретті апериодты буынмен және таза кешігу буынымен және таза кешігу буынымен көрсетсек, есебіміз жеңілдейді.
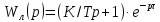(10.40)
мұнда
;
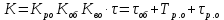
K, T,
- сандық мәндерін нақты нысанның мысалын қарастырғанда анықтаймыз.
Осындай талдап қорытындылау нәтижесінде екіпозициалық реттеуіші және басқару нысаны бар түзусызықсыз жүйені аламыз, ал оны зерттеу үшін гармоникалық сызықтандыру әдісін қолданамыз.
Бұл әдістің мәнісі – елеулі түзусызықсыз элементті тепе-тең (эквивалентті) сызықты буынмен алмастыру.
Тепе-теңдік шарты ретінде тепе-тең буынның шығыстық сигналының амплитудасы мен фазасының нақты түзусызықсыз элементтің шығысындағы сигналдың бірінші гармоникаға теңдігі алынады.
Гармоникалық сызықтандырудың кәдімгі сызықтандырудан принциті айырмашылығы бар, өйткені сызықтандырылған элементтің коэффициенттері тұрақты емес және олар кірістік сигналдың амплитудасына тәуелді.
Гармоникалық сызықтандыру коэффициенттері түзусызықсыз түрлеріне байланысты болады.
Мысалы, сезімталсыз аймақты екіпозициялық реттеуіштің беріліс функциясын мына өрнекпен анықтауға болады:
, (10.41)
мұндағы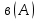
және 
болғандағы сызықтандыру коэффициенттері.
;
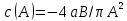(10.42)
мұндағы
және b реттеуіштің (түзусызықсыз элементінің) статистикалық сипаттамасының параметрлері.
Р-ны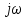
ауыстырып түзусызықсыз элементтің АФЖС үшін өрнек аламыз
(10.43)
Егер жүйенің сызықты бөлімі жоғары ретті теңдеумен сипатталса нмесе кешігуі болса, онда автотербелістің параметрлерін анықтау үшін Найквист критерийі пайдаланылады. Автотербелістердің болу шарты мына теңдікпен анықталады:
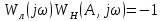(10.44)
немесе
(10.45)
мұндағы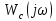
- жүйенің барлық сызықты буындарының АФЖС, ал оң жақтағы – түзусызықсыз элементтің теріс таңбалы кері сипаттамасы.
Бұл теңдеуді графикалық жолмен шешу ыңғайлы болады. Ол үшін сызықты бөлімінің АФЖС және түзусызықсыз элементтің кері сипаттамасын бір координаттық жүйеде тұрғызу керек. Қисық сызықтардың қиылысқан нүктелерінде автотербелістің параметрлерін анықтайды.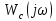 қисығында автотербелістің жиілігін, 
а-ны, ал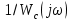 
қисығында автотербелістің амплитудасын Аа-ны анықтайды.
Автотербеліс режимінің орнықтылығы немесе орнықсыздығы фактісі келесі ереже көмегімен табылады: егер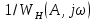
қисығында жатқан қиылысу нүктесіне жақын, бірақ А параметрінің өсу бағытына жылжыған нүкте, 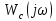сипаттамасымен қамтылса, онда автотербеліс орнықты, ал егер қамтылмаса, автотербеліс орнықсыз.
Реттеуішті баптау параметрлерін есептеу
Реттеу заңын таңдап алып және жүйенің орнықтылығына талдау жүргізгеннен соң реттеуіштің баптау параметрлерін негіздеу керек болады. Бұл есептеулерді жүргізудің бірнеше әдістері бар. Реттеуіштің оңтайлы параметрлерін есептеу оның типіне және жүйедегі өтпелі үрдіске байланысты жүргізіледі. Түзусызықсыз релелік (позициялық) реттеуішті автоматты жүйелердегі өтпелі үрдістің сипаты, релелік элементтің статистикалық сипаттамасымен, нысанның түрімен (статистикалық, астатикалық, кешігумен, кешігусіз) анықталады.
Қарастырылып отырған нысан кешігулі апериодтық буын болып табылады, ал реттеуіш – екіпозициялық сезімталдықсыз аймақты реттеуіш болады. Бұл жағдайда реттелетін шаманың (температураның) ауытқу диапазоны реттеуіштің бірмәнсіздік аймағынан үлкен болады, өйткені реттеуіш реттелетін шаманың нақтылы өзгеруіне кешігуімен әсерлестік көрсетеді.
Автотербелістер амплитудаларының t1 және теріс t2 ұзақтықтарын, олардың периодын Т, реттуіштің ауыстырып қосылу жиілігін n1 реттелетін шаманың берілген мәннен ауытқуының
х1 оң және х2 теріс амплитудаларын, реттелетін шаманың ауытқуы ∆х диапазонын есептеуге арналған өрнектер әдебиеттерде берілген.
Екіпозициялық реттеуіштің беріліс функциясы
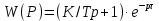(10.45)
болатын статистикалық нысан үшін статистиалық сипаттамаларды келесі өрнектер бойынша есептеуге болады:
1-жағдай
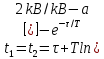
Tk=2t1; n=2/Tk;
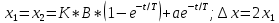
2- жағдай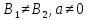
:
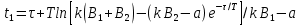
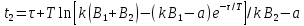
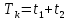
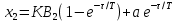
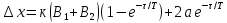
Басқарылатын шаманың берілген мәнге қатысты ауытқуларының амплитудасларының теңдіктеріне, реттеуішті практика жүзінде баптағанда, реттелетін шаманың берілген мәнін дәлдеу арқылы қол жеткізіледі. Реттеуіштің тапсырмасын мынадай шамаға дәлдеу керек.
(10.47)
Қарастырылған өрнектерден мынадай тұжырымдар жасаймыз: бірмәнсіздік аймағы 2а-ның азаюы, тербеліс периодының Тк азаюына және реттеуіштің ауыстырып қосылу санының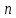
көбеюіне әкеліп соғады.
Ауыстырып қосу санының азаюы, реттеуіш айырып-қосатын энергия көлемі арқылы (электр калорифердің қуаты) азаюы мүмкін. Мұның өзінде ескеретін жәйт, реттеуіштің реттеуші ықпалдары нысанға әсер ететін мүмкін қоздырма ықпалдарды толығымен өтемдеу керек.
Нысанның уақыт тұрақтысының артуы, барлық басқа теңдік жағдайларда тербелістер периодын ұлғайтады және реттеуіштің ауыстырып қосу жиілігін азайтады.
Түзусызықсыз жүйенің өзіндік ерекшелігі болып автотербеліс режимі табылады. Автотербелістер түзусызықсыз жүйелерге орнықты жұмыс режимі болады. Мысалы, түзусызықсыз басқарушы құрылғысы бар температураны автоматты түрде тұрақтандыру жүйесі. Түзусызықсыз жүйелерді талдағанда мынадай міндеттер шешіледі:
− жүйенің мүмкін болатын тепе-теңдік қалыптарын іздестіру және олардың орнықтылығын бағалау;
− автотербеліс параметрлерін және олардың жүйенің параметрлерімен байланысын анықтау.
Әдетте, түзусызықсыз жүйеде бір елеулі түзусызықсыз элемент болады.
Сызықты бөлім өзіне барлық сызықты немесе сызықтандырылған сипаттамалы элементтерді жинастырады және кез келген күрделі құрылымда бола алады.
Қарастырылып отырған жүйеде түзусызықсыз элементіміз температураның екіпозициялық реттеуіші, ал сызықты бөлім реттеуіш органнан (РО), басқару нысанынан (БО) және қабылдаушы органнан (ҚО) құралады.
Жүйенің орнықтылығын талдау
Автоматты басқару жүйесінің ең бір маңызды сипаттамасы, оның орнықтылығы. Орнықсыз жүйе жұмысқа жарамсыз, яғни ол басқару қызметтерін орындауға қабілетсіз және басқарылатын нысанды апаттық жағдайда алып келуі мүмкін. Кез келген практикалық жүйе орнықты болуы керек.
Нақты автоматты басқару жүйелерінің орнықтылық шарттарын А.М.Ляпунов тұжырымдады:
-
Егер сызықты АБЖ орнықсыз болса, онда нақты АБЖ-де орнықты болады, соның өзінде сызықтандыру кезінде алып тасталған қандай да бір мүшелер оның орнықтылығын өзгерте алмайды. -
Егер сызықты АБЖ орнықсыз болса, онда нақты АБЖ-де орнықсыз, соның өзінде сызықтандыру кезенде алып тасталған ешқандай мүшелер оның орнықтылығын өзгерте алмайды.
Осыған байланысты, беріліс функциясы төмендегідей жүйенің, сызықты бөлімінің орнықтылығына көз жеткізу керек.
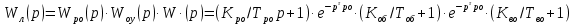(10.31)Таза кешігуі бар екі буынды біріктіргенде алатынымыз:
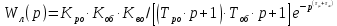(10.32)Басқару жүйесінің контурында кешігу буыны болғанда жүйенің сипаттамалық теңдеуі трансценденттік болады, ал оларды шешу үлкен қиындықтар тудырады. Сондықтан практикалық есептерде трансценденттік беріліс функцияларын Пад қатарына жіктейді. Қатардың екі немесе үш мүшелерін ғана есепке алып, беріліс функциясын шамалап бөлшек рационал функциямен алмастырады
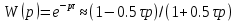(10.33)мұндай ауыстыру қанағаттанарлық жуықтау береді, тек егер кірістегі сигналдың жиілігі
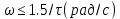(10.34)Кешігу буынын жуықтап апроксимациялаудың басқа тәсілі, оны уақыт тұрақтылары бірдей
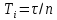бірнеше бірінші ретті инерциялық буындардың тізбектей жалғануы түрінде көрсету. 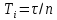(10.35) 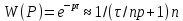(10.36)Қарастырылып отырған жүйеге жоғары дәлдікті аппроксимация керексіздігін ескеріп, кешігу буынын беріліс функциясы төмендегідей бір ғана инерциялық буынмен алмастырамыз:
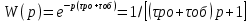(10.37)Тиісінше жүйенің сызықты бөлімінің беріліс функциясының өрнегі:
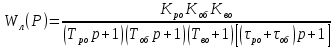(10.38)қосындыны
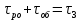, белгілейміз.Сызықты бөлімнің беріліс функциясын стандарттық формада жазамыз:
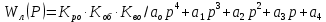(10.39)мұндағы
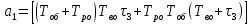
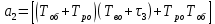
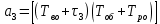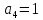
; ; Гурвиц немесе Раус критерийлерін пайдаланып, сызықты жүйенің орнықтылығын анықтаймыз. Есептейлерді нақты жүйенің орнықтылығын анықтаған мысалда қарастырамыз. Жүйенің сызықты бөлімі орнықты болған жағдайда тұтас жүйенің орнықтылығын анықтауға көшеміз.
Түзусызықсыз жүйелердің орнықтылығын анықтау үшін (басқа әдістермен қатар) гармоникалық сызықтандыру (линериализация) әдісі қолданылады.
Гормоникалық сызықтандыру әдісі жуықтау әдіс, ол автотербелістерді туындау жағдайын және параметрлерді анықтауға мүмкіндік береді.
Жүйенің сипаттамалық полиномының реті жоғары болғанда, бұл әдіс едәуір есептеулерді талап етеді. Ал егер жүйенің сызықты бөлімін, яғни реттеулеріне қарасты өздігінен теңесетін біріккен статистикалық нысан болатын бөлімді, тізбектей қосылған бірінші ретті апериодты буынмен және таза кешігу буынымен және таза кешігу буынымен көрсетсек, есебіміз жеңілдейді.
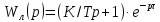(10.40)мұнда
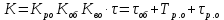
; K, T,
- сандық мәндерін нақты нысанның мысалын қарастырғанда анықтаймыз.Осындай талдап қорытындылау нәтижесінде екіпозициалық реттеуіші және басқару нысаны бар түзусызықсыз жүйені аламыз, ал оны зерттеу үшін гармоникалық сызықтандыру әдісін қолданамыз.
Бұл әдістің мәнісі – елеулі түзусызықсыз элементті тепе-тең (эквивалентті) сызықты буынмен алмастыру.
Тепе-теңдік шарты ретінде тепе-тең буынның шығыстық сигналының амплитудасы мен фазасының нақты түзусызықсыз элементтің шығысындағы сигналдың бірінші гармоникаға теңдігі алынады.
Гармоникалық сызықтандырудың кәдімгі сызықтандырудан принциті айырмашылығы бар, өйткені сызықтандырылған элементтің коэффициенттері тұрақты емес және олар кірістік сигналдың амплитудасына тәуелді.
Гармоникалық сызықтандыру коэффициенттері түзусызықсыз түрлеріне байланысты болады.
Мысалы, сезімталсыз аймақты екіпозициялық реттеуіштің беріліс функциясын мына өрнекпен анықтауға болады:
, (10.41)мұндағы
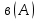және болғандағы сызықтандыру коэффициенттері. ; 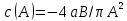(10.42)мұндағы
және b реттеуіштің (түзусызықсыз элементінің) статистикалық сипаттамасының параметрлері.Р-ны
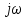ауыстырып түзусызықсыз элементтің АФЖС үшін өрнек аламыз (10.43)Егер жүйенің сызықты бөлімі жоғары ретті теңдеумен сипатталса нмесе кешігуі болса, онда автотербелістің параметрлерін анықтау үшін Найквист критерийі пайдаланылады. Автотербелістердің болу шарты мына теңдікпен анықталады:
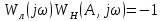(10.44)немесе
(10.45)
мұндағы
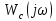- жүйенің барлық сызықты буындарының АФЖС, ал оң жақтағы – түзусызықсыз элементтің теріс таңбалы кері сипаттамасы.Бұл теңдеуді графикалық жолмен шешу ыңғайлы болады. Ол үшін сызықты бөлімінің АФЖС және түзусызықсыз элементтің кері сипаттамасын бір координаттық жүйеде тұрғызу керек. Қисық сызықтардың қиылысқан нүктелерінде автотербелістің параметрлерін анықтайды.
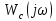қисығында автотербелістің жиілігін, а-ны, ал 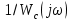қисығында автотербелістің амплитудасын Аа-ны анықтайды.Автотербеліс режимінің орнықтылығы немесе орнықсыздығы фактісі келесі ереже көмегімен табылады: егер
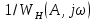қисығында жатқан қиылысу нүктесіне жақын, бірақ А параметрінің өсу бағытына жылжыған нүкте, 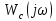сипаттамасымен қамтылса, онда автотербеліс орнықты, ал егер қамтылмаса, автотербеліс орнықсыз.Реттеуішті баптау параметрлерін есептеу
Реттеу заңын таңдап алып және жүйенің орнықтылығына талдау жүргізгеннен соң реттеуіштің баптау параметрлерін негіздеу керек болады. Бұл есептеулерді жүргізудің бірнеше әдістері бар. Реттеуіштің оңтайлы параметрлерін есептеу оның типіне және жүйедегі өтпелі үрдіске байланысты жүргізіледі. Түзусызықсыз релелік (позициялық) реттеуішті автоматты жүйелердегі өтпелі үрдістің сипаты, релелік элементтің статистикалық сипаттамасымен, нысанның түрімен (статистикалық, астатикалық, кешігумен, кешігусіз) анықталады.
Қарастырылып отырған нысан кешігулі апериодтық буын болып табылады, ал реттеуіш – екіпозициялық сезімталдықсыз аймақты реттеуіш болады. Бұл жағдайда реттелетін шаманың (температураның) ауытқу диапазоны реттеуіштің бірмәнсіздік аймағынан үлкен болады, өйткені реттеуіш реттелетін шаманың нақтылы өзгеруіне
кешігуімен әсерлестік көрсетеді.Автотербелістер амплитудаларының t1 және теріс t2 ұзақтықтарын, олардың периодын Т, реттуіштің ауыстырып қосылу жиілігін n1 реттелетін шаманың берілген мәннен ауытқуының
х1 оң және х2 теріс амплитудаларын, реттелетін шаманың ауытқуы ∆х диапазонын есептеуге арналған өрнектер әдебиеттерде берілген.
Екіпозициялық реттеуіштің беріліс функциясы
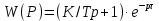(10.45)болатын статистикалық нысан үшін статистиалық сипаттамаларды келесі өрнектер бойынша есептеуге болады:
1-жағдай
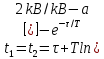
Tk=2t1; n=2/Tk;
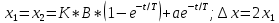
2- жағдай
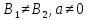
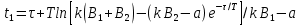
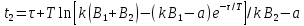
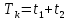
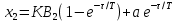
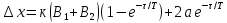
: Басқарылатын шаманың берілген мәнге қатысты ауытқуларының амплитудасларының теңдіктеріне, реттеуішті практика жүзінде баптағанда, реттелетін шаманың берілген мәнін дәлдеу арқылы қол жеткізіледі. Реттеуіштің тапсырмасын мынадай шамаға дәлдеу керек.
(10.47)Қарастырылған өрнектерден мынадай тұжырымдар жасаймыз: бірмәнсіздік аймағы 2а-ның азаюы, тербеліс периодының Тк азаюына және реттеуіштің ауыстырып қосылу санының
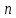көбеюіне әкеліп соғады.Ауыстырып қосу санының азаюы, реттеуіш айырып-қосатын энергия көлемі арқылы (электр калорифердің қуаты) азаюы мүмкін. Мұның өзінде ескеретін жәйт, реттеуіштің реттеуші ықпалдары нысанға әсер ететін мүмкін қоздырма ықпалдарды толығымен өтемдеу керек.
Нысанның уақыт тұрақтысының артуы, барлық басқа теңдік жағдайларда тербелістер периодын ұлғайтады және реттеуіштің ауыстырып қосу жиілігін азайтады.