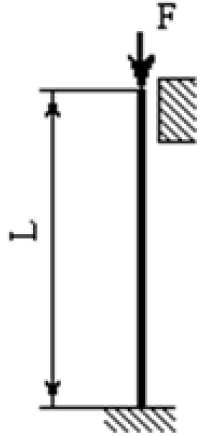
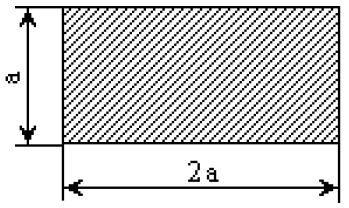
Расчет на устойчивость сжатого стержняИсходные данные: F = 65 кН; l = 3,5 м; [σ] = 10 МПа; Е ; λ_nц=60; способ закрепления – 4; материал – сосна; а= 40 МПа; b=0,203 МПа.На рисунке 1 показана заданная схема закрепления стержня.Рисунок 1 – Заданная схема закрепления стержняНа рисунке 2 показана заданная форма поперечного сечения стержня.Рисунок 2 – Форма поперечного сеченияРешение1 Определяем основные геометрические характеристики сечения стойки.Определяем площадь сечения по формуле:

	(1)

после подстановки численных значений, получим

	(2)

где – коэффициент площади, применяемый при расчете на ЭВМ;-осевой момент инерции сечения вычисляем по формуле

	(3)

подставляя числовые значения, получимгде – коэффициент минимального момента инерции для расчёта на ЭВМ.-минимальный радиус инерции определяем по формуле

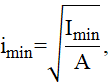(4)

подставляя числовые значения, получим

---

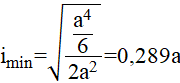
или

	(5)

где – коэффициент минимального радиуса инерции для расчета на ЭВМ.2 Производим проектировочный расчёт размеров сечения методом повторных приближений.I приближение. Задаёмся коэффициентом продольного изгиба .По условию устойчивостиопределяем расчётную площадь по формуле

	(6)

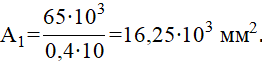
Подставляя числовые значения, получим (при )Используя формулу (2)определим размер поперечного сечения стойки

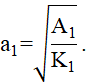(7)

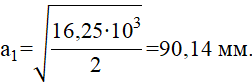
Подставляя числовые значения, получимОпределяем минимальный радиус инерции по формуле (5)Подставляя числовые значения, получимОпределяем расчётную гибкость стержня по формуле

	(8)

---

где – коэффициент приведения длины; для заданной стойки (рисунок 1) ;подставляя числовые значения, получимОпределяем коэффициент продольного изгибаСравнивая с , видим, что эти значения отличаются друг от друга более чем на 5 %, т.е.Аналогично вышеизложенной последовательности проводим расчет по второму приближению. Для этого принимаем коэффициент продольного изгиба, рассчитав его среднее значение по величинам первого приближенияРезультаты расчётов записываем в таблицу 1.Таблица 1 – Результаты расчета 1-7 приближений

Номер приближения		, мм2	, мм	, мм
1	0,4	16,25	90,14	26,05	268,71	0,14
2	0,27	24,07	109,70	31,70	220,82	0,14
3	0,205	31,71	125,92	36,39	192,36	0,14
4	0,1725	37,68	137,26	39,67	176,46	0,14
5	0,1563	41,59	144,20	41,67	167,99	0,14
6	0,1482	43,86	148,09	42,80	163,55	0,14
7	0,1441	45,11	150,18	43,40	161,29	0,14

---

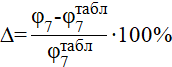
Расхождение результатов расчета коэффициента в седьмом приближении равноиличто меньше 5 %, т.е. является допустимым.Согласно ГОСТ 6636-69 окончательно принимаем , тогда3 Определяем коэффициент запаса устойчивости стержня по формуле

(9)

Здесь критическое напряжение определяем, как для стержней большой гибкости, т.к. выполняется следующее условие:т.е. по формуле Эйлера

	(10)

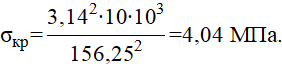
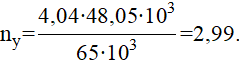
Подставив числовые значения, получимОпределяем коэффициент запаса устойчивости, подставив числовые значения в формулу (9)Таким образом, видим, что коэффициент запаса устойчивости больше единицы, что обусловливает работоспособность стойки по критерию устойчивости.Определим удельный радиус инерции по формуле

(11)

После подстановки, получим

---

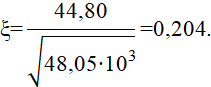
Полученная незначительная величина удельного радиуса инерции (т.е. меньше 1,0) позволяет заключить, что заданное сечение является не целесообразным с позиции теории устойчивости сжатых стержней.

---

Смотрите также файлы

• Учебников Горизонты.docx

• Мкоу Путьильичёвская сош Палласовский муниципальный район.pptx

• Антитеррористическая деятельность Российской Федерации правовые основы, силы и средства.docx

• Стеганография двоичная тайнопись.doc

• Строительство школы на 250 мест.docx