МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИОрдена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования«Московскийтехническийуниверситетсвязииинформатики»Кафедра «Информатика»Лабораторная работа №1«Методы решения нелинейных уравнений»по дисциплине«Численные методы»Выполнил студент гр. БИН2104:Диев Е. С.Проверил: Москва, 2023 г.Содержание.

1. Общее задание.

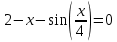
В данной лабораторной работе необходимо исследовать функцию нелинейного уравнения, данную по вариантам. В этом случае будет исследоваться уравнение 6-го варианта:В этом уравнении необходимо найти корни уравнение двумя методами:

1. 
   методом хорд;
   
2. 
   методом половинного деления.
   

Также необходимо проверить погрешность и написать программу для анализа уравнения.

2. Ход работы.

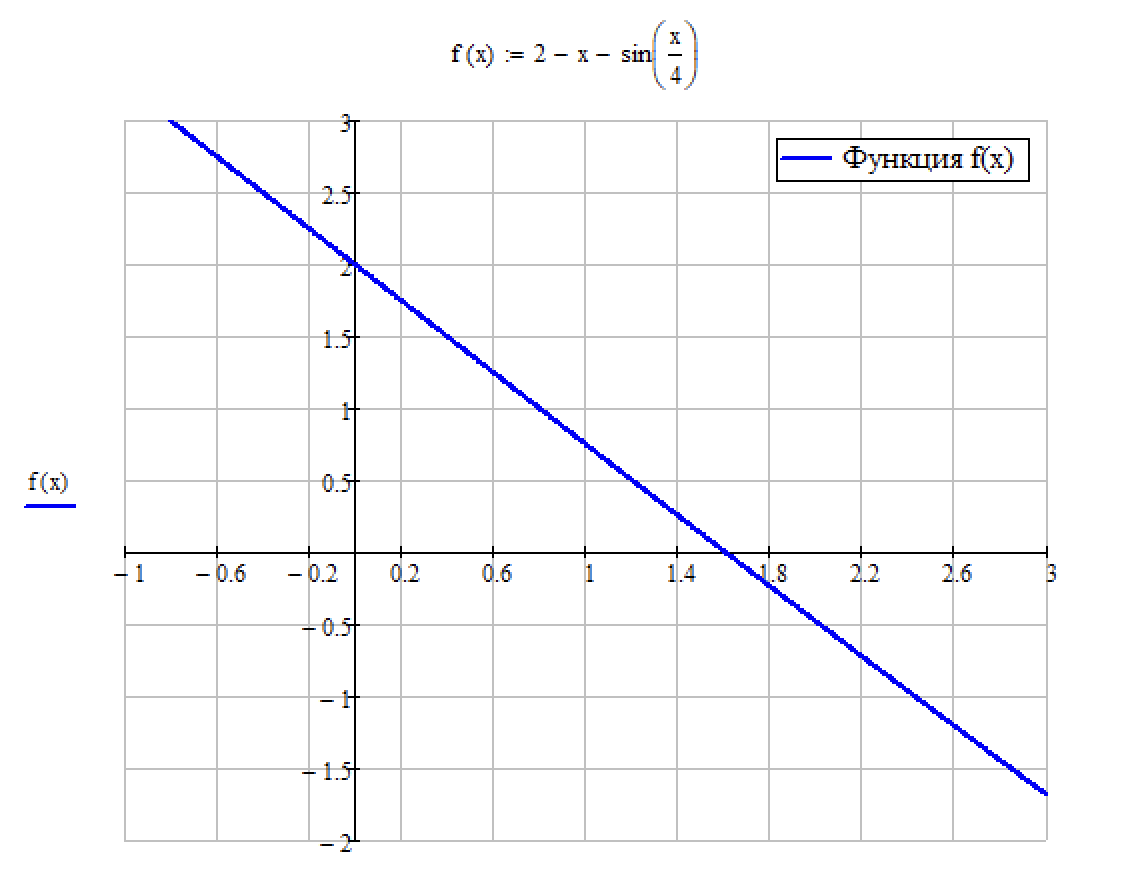
Вся работа будет производится в математическом пакете Mathcad 15. Первым делом переносим данную функцию и строим её график (рис. 1)Рисунок 1. – График функции 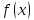(графический метод отделения корня .

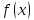3. Этап отделения корней.

Переходим к этапу отделения корней. Для этого необходим как графический метод, так и аналитический. График уже построен выше (рис. 1), а аналитический метод представлен ниже (рис. 2).

---

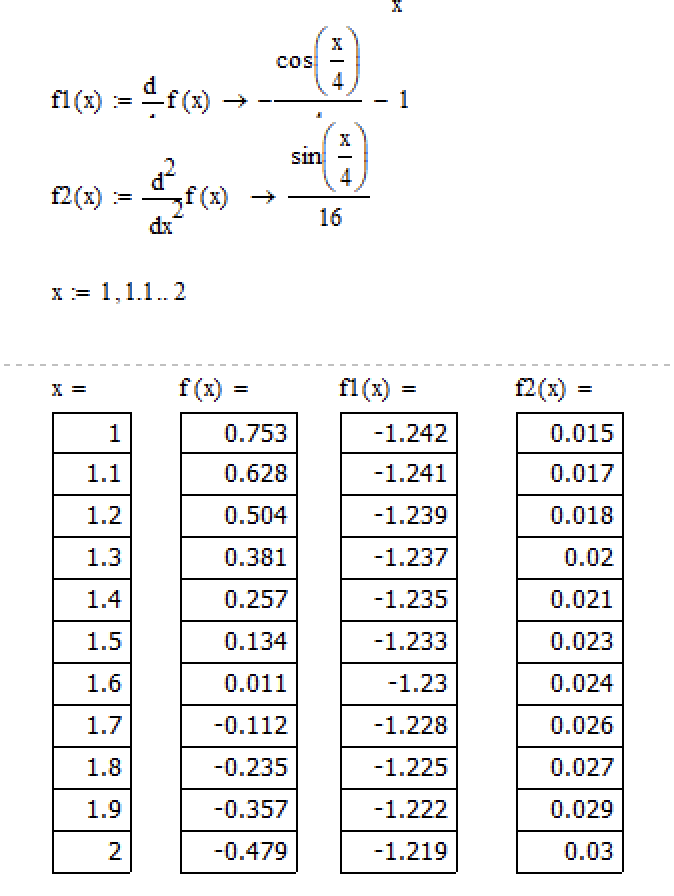
Рисунок 2. – Аналитический метод отделения корня , таблица первых и вторых производных функции , её значения и значения 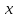.На графике функции видно, что корень один (там, где он пересекает ось абсцисс). Это промежуток 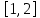.Для аналитического метода понадобится таблица первых и вторых производных функции , её значения и значения 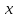(рис. 2) Выбранный шаг – 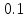, поэтому 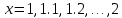. Можно заменить, что значение меняет свой знак на значении 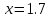из чего можно сделать вывод, что в промежутке 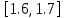существует единственный корень данного уравнения.Значения первой производной 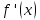, не меняется на протяжении всего промежутка 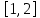, т. к. функция всегда убывает. Можно сделать вывод, что убывает всегда, хоть это и не совсем корректно.Значения первой производной 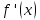и второй производной 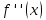будут использоваться в дальнейшем в методе хорд.

4. Этап уточнения корней (метод хорд).

Необходимые и достаточные условия сходимости для метода хорд:

1. 
   непрерывна на 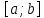и ;
   
2. 
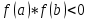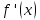   и 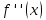отличны от нуля и сохраняют знаки для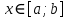
   

---

Проверим условия сходимости на промежутке (рис. 3).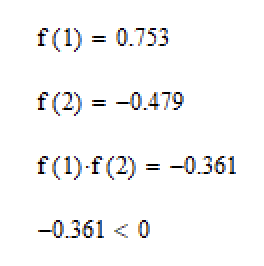Рисунок 3. – Проверка условия сходимости. Видно, что условие выполняется. Второе требование может быть проверено по полученной нами ранее таблице (рис. 2) где видно, что и отличны от нуля и сохраняют знаки для . Условия сходимости выполняются.Для вычисления методом хорд воспользуемся следующей рекуррентной формулой: 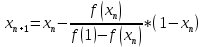;Расчёт в Mathcad 15 показан ниже (рис. 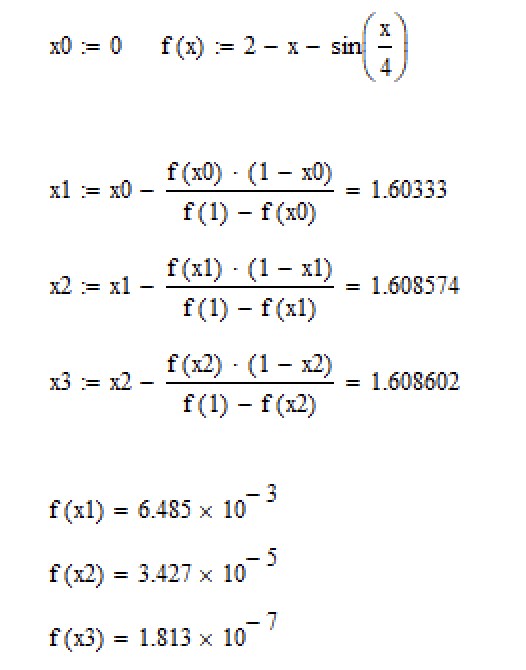4).Рисунок 4. – Расчёт метода трёх хорд в Mathcad. Построим таблицу по полученным данным (табл. 1).Таблица 1. – Результаты расчёта методом трёх хорд в Mathcad.

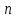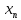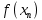0	0	2
1	1.60333	0.006485
2	1.608574	0.00003427
3	1.608602	0.0000001813

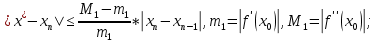
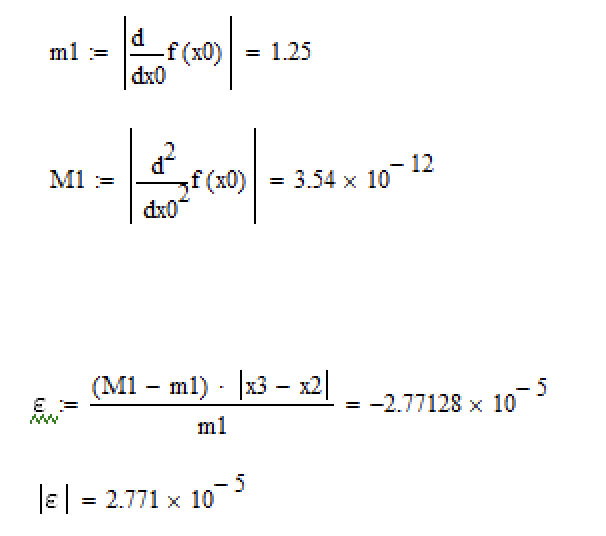
Оценим погрешность этих вычислений по этой формуле:Расчёт в Mathcad 15 показан ниже (рис. 5).Рисунок 5. – Расчёт погрешности в Mathcad.Полученная погрешность 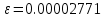, что достаточно мало.

1. Этап уточнения корней (метод половинного деления).

---

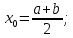
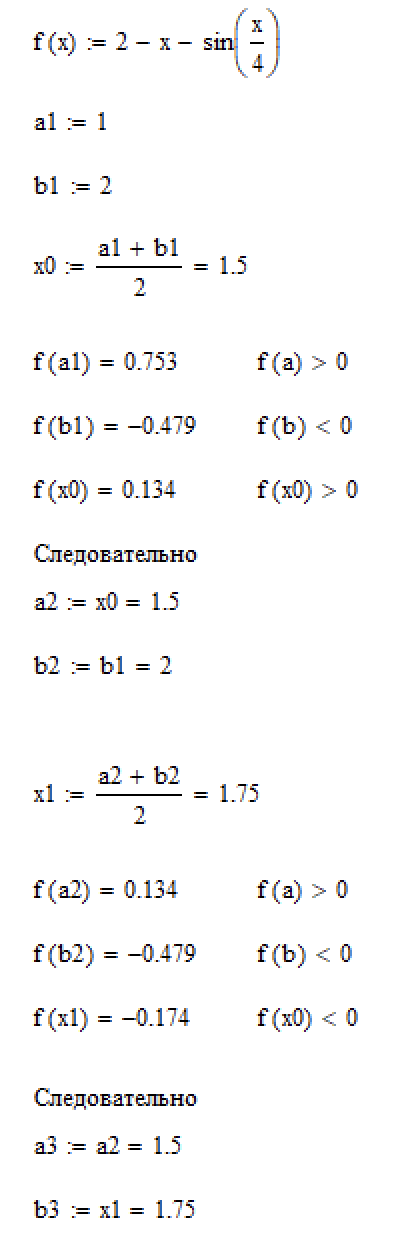
Необходимое и достаточное условие сходимости для метода половинного деления одно: если на отрезке существует только один корень. Это действительно так, так что условие сходимости уже доказано.Выбираем начальное приближение. Это делается по следующей формуле:Приближаем так три раза. Все расчёты из Mathcad 15 представлены ниже (рис. 6.1 и рис. 6.2)Рисунок 6.1. 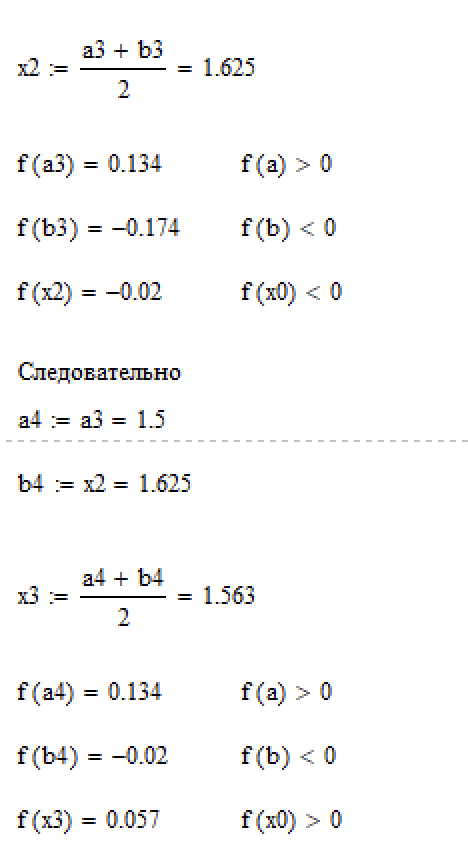– Расчёт первых двух итераций метода половинного деления в Mathcad.Рисунок 6.2. – Расчёт последней итераций метода половинного деления в Mathcad.Из последней итерации видно, что корень уравнения 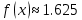. Число схоже с первым методом хорд, но гораздо менее точное. Внесём все результаты в таблицу (см. таблицу 2).Таблица 2. – Результаты расчёта методом половинного деления в Mathcad.

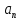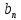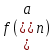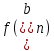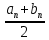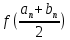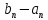0	1	2	0.753	-0.479	1.5	0.134	-1
1	1.5	2	0.134	-0.479	1.75	-0.174	-0.5
2	1.5	1.75	0.134	-0.174	1.625	-0.174	-0.25
3	1.5	1.625	0.134	-0.02	1.5625	-0.02	-0.125

---

Реализуем данный метод с помощью языка программирования C++. Программный код представлен ниже (см. листинг 1).#include

#include
double fx(double x)

{

double function = 2 - x - sin(x/4);

return function;

};
int main()

{

double a, b, c, e;

std::cout << "[a] Введите нижнюю границу промежутка > ";

std::cin >> a;

std::cout << "[b] Введите верхнюю границу промежутка > ";

std::cin >> b;

std::cout << "[e] Задайте точность (чем меньше число, тем точнее) > ";

std::cin >> e;

while (b - a > e)

{

c = (a + b)/2;

if (fx(b) * fx(c) < 0)

{

a = c;

}

else

{

b = c;

}

}

std::cout << (a + b)/2 << "\n";

return 0;

}

Листинг 1. – Программный код для реализации метода половинного деления на языке C++.
Данная программа получает на вход три значения: 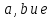. 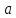и 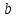– переменные, обозначающие верхний и нижний пределы промежутка, а 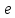– точность, с которой вычисляется корень уравнения.
В ручном расчёте точность можно вычислить по формуле:

;

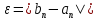Исходя из выше полученных данных (табл. 1) точность расчёта третий итерации равна .
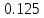Проверим программу на работоспособность, написав туда необходимые значения ( 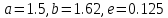). Вывод программы показан ниже (рис. 7).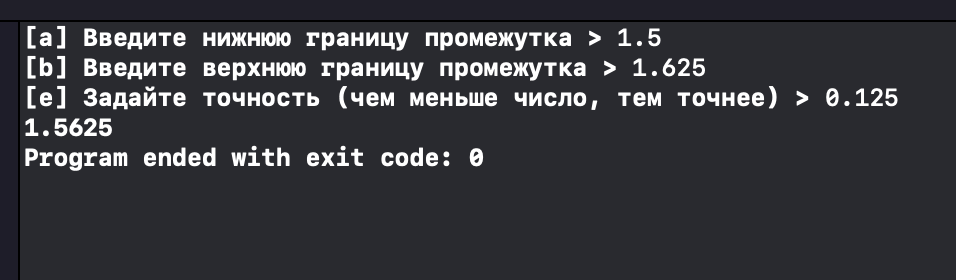


Рисунок 7. – Вывод программы.
Значение совпадает с тем, которое было получено ручным счётом, что говорит о правильности написания программы.

5. Вывод.

Были выполнены все необходимые задания, поставленные в лабораторной работе, корни уравнения были отделены графическим и аналитическим методами и найдены методами хорд и половинного деления.

---

Смотрите также файлы

• Информационные компьютерные модели.pdf

• Теории возникновения государства.doc

• Введение в экономику организации.docx

• Время отдыха.docx

• Воспитания и социализации.docx