ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 317
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
5 и правилу 1 введения квантора общности.
Так доказана истинность формулы x(P3(x)(P2(x))).
На рис. 12 приведен граф, иллюстрирующий процесс дедуктивного вывода.
x( P1(x)( P2(x)))
x(P3 (x)P1 (x))


(P1 (t)( P2 (t)))
P3 (t) P1 (t)
(P3 (t)( P2 (t)))
x(P3(x)(P2(x)))
Рис. 12. Граф вывода заключения
Пример: Доказать истинность заключения
 x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))); x(P3(x))
x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))); x(P3(x))
x(P3(x))xy(P21.(x; y)(P2(y))).
1) F1=x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))) - посылка;
2) F2= x(P3(x)) -посылка;
3) F3=x(P3(x)) - заключение no формуле F2 и правилу 5) смены кванторов (закон де Моргана);
4) F4=P3 (t) - заключение по формуле F3 и правилу 2) удаления квантора общности;
5) F5=P3(t)P24.(x;t) - заключение по формуле F4 и правилу 4) исчисления высказываний;
6) F6=y(P3(y)(P24 (x; y))) - заключение по формуле F5 и правилу 1) введения квантора общности;
7) F7=y(P3(y)P24 (x; y)) - заключение по формуле F6 и правилу смены кванторов (закон де Моргана);
8) F8=y(P21.(t; y)P2(y)y(P3(y)P24.(t; y)) - заключение по формуле F1 и правилу 2) удаления квантора общности;
9) F9= y(P21.(t; y)P2(y)) - заключение пo формулам F7 и F8 при условии t=x и правилу modus tollens;
10) F10=y( P21.(t; y)P2(y)) - заключение по формуле F9 и правилу смены кванторов (закон де Моргана);
11) F11=y(P21. (t; y) (P2
(y)) - заключение пo формуле F10 и эквивалентным преобразованиям алгебры предикатов;
12) F12=xy(P21. (x; y) (P2 (y)) - заключение по формуле F11 и правилу 1) введения квантора общности;
13) x(P3(x))xy(P21.(x; y)( P2(y))) – заключение по формулам F2 и F12 и правилу modus ponens. Что и требовалось доказать.
x(P3(x))
x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y)))
На рис. 13 приведен граф вывода этой задачи.

x(P3(x))
y(P21.(t; y)P2(y)y(P3(y)P24.(t; y))




P3 (t)
y(P21.(t; y)P2(y))

P3(t)P24.(x;t)
y( P21.(t; y)P2(y))


y(P21. (t; y) (P2 (y))
y(P3(y)(P24 (x; y)))

y(P3(y)P24 (x; y))
xy(P21. (x; y) (P2 (y))

x(P3(x))xy(P21.(x; y)( P2(y)))

рис. 13 Граф вывода заключения
Пример. Доказать истинность заключения
 x(P1(x)y(P2(y)P24.(x; y))); x(P1(x)y(P3(y)P24.(x; y)))
x(P1(x)y(P2(y)P24.(x; y))); x(P1(x)y(P3(y)P24.(x; y)))
x(P2(x)P3(x)).
1) F1=x(P1(x)y(P2(y)P24.(x; y))) - посылка;
2) F2=x(P1(x)y(P3(y)P24 (x; y))) - посылка;
3) F3=P1(а)y(P2(y)P24.(a; y))-заключение по формуле F1, правилу формирования ССФ;
4) F4=P1(a)- заключение по формуле F3 и правилу удаления конъюнкции исчисления высказываний
5) F5=y(P2(y) P24.(a; y)) - заключение пo формуле F3 и правилу удаления конъюнкции исчисления высказываний;
6) F6=P2(t) P24.(a; t) - заключение по формуле F5 и правилу 2) удаления квантора общности;
7) F7=P1(t)y(P3(y)P24 (t; y)) - заключение по формуле F2 и правилу 2) удаления квантора общности;
8) F8=y(P3(y) P24 (a; y)) - заключение по формулам F3 и F7 при t=a и правилу modus ponens;
9) F9=P3(t)P24.(a; t) - заключение по формуле F8 и правилу 2) удаления квантора общности;
10) F10=P24.(a; t)P3(t) - заключение по формуле F9 и закону контрапозиции (правило 8) исчисления высказываний);
11) F11=P2(t)P3(t) - заключение по формулам F6 и F10 и закону силлогизма (правило 11) исчисления высказываний);
12) F12=x( P2 (x)P3(x)) - заключение по формуле F11 и правилу 1) введения квантора x. Что требовалось доказать.
На рис. 14 приведен граф вывода этой задачи.
x(P1(x)y(P2(y)P24 (x; y)))
x(P1(x)y(P3(y)P24.(x; y)))

 x=a
x=a
P1(а)y(P2(y)P24.(a; y))
P1(t )y(P3(y)P24 (t; y))


P1(a)
y(P2(y) P24.(a; y))
P1(a )y(P3(y)P24 (a; y))


y(P3(y) P24 (a; y))
P2(t) P24.(a; t)
P3(t)P24.(a; t)
P24.(a; t)P3(t)



P2(t)P3(t)
x( P2 (x)P3(x))
Рис. 14. Граф вывода заключения
2.2.4 Принцип резолюции
Если матрица формулы в результате приведения к виду ПНФ не будет содержать свободных переменных и сколемовских функций, то для вывода заключения полностью пpuменим алгоритм принципа резолюции, рассмотренный в исчислении высказываний. Этот алгоритм основывается на том, что если две формулы состоящие из дизъюнкции атомов (в дальнейшем такие формулы будем называть дизъюнктами ) связаны конъюнкцией, и в них имеются два одинаковых или приводимых к одинаковым (унифицируемых ) атома с разными знаками, то из них можно получить третий дизъюнкт , который будет логическим следствием первых двух, и в нем будут исключены эти два атома. Однако, если в результате приведения к виду ССФ аргументы атомов содержат сколемовские функции, то для поиска контрарных атомов необходимо выполнить подстановки термов вместо предметных переменных и получить новые формулы дизъюнктов, которые допускают их унификацию при формировании контрарных пар. Множество подстановок нужно формировать последовательно, просматривая каждый раз только одну предметную переменную.
Например, если даны два дизъюнкта (P1(x)P2(x)) и (P1(f(x))P3(y)), то для получения контрарной пары атомов возможна подстановка
xf(х)(P1(x)P2(x))=(P1(f(x))P2(f(x))) и
xf(х)(P1(f(x))P3(y))= (P1(f(x))P3(y)).
В результате склеивания этих дизъюнктов может быть получена резольвента: (P1(f(x))P2(f(x)))(P1(f(x))P3(y))= (P2(f(x)) P3(y)).
Если пара дизъюнктов имеет вид (P1(f1(x))P2(x)) и (P1(f2(x))P3(y)), то никакая подстановка не позволит сформировать резольвенту.
Пример: Даны две формулы P3(a;x;f(q(y))) и P3(z;f(z);f(u)).
Выполнить унификацию контрарных атомов.
1) za P3(z;f(z);f(u))=P3(a;f(a);f(u));
2) xf(a) P3(a;x;f(q(y)))=P3(a;f(a);f(q(y)));
3) uq(y) P3(a;f(a);f(u))=P3(a;f(a);f(q(y))).
В результате получены два контрарных атома: P3(a;f(a);f(q(y))) и P3(a;f(a);f(q(y))). Если в эти формулы атомов вместо предметной переменной y сделать подстановку предметной постоянной b, т.е.
ybP3(a;f(a);f(q(y)))=P3(a;f(a);f(q(b))) и
ybP3(a;f(a);f(q(y)))= P3(a;f(a);f(q(b))),
то получим два контрарных высказывания.
Пример. Даны две формулы P3(x;a;f(q(a))) и P3(z;y;f(u)).
Выполнить унификацию контрарных формул.
1) xbP3(x;a;f(q(a)))=P3(b;a;f(q(a)));
2) ya P3(z;y;f(u))=P3(z;a;f(u));
3) yaP3(z;a;f(u))=P3(b;a;f(u));
4) uq(a)P3(b;a;f(u))=P3(b;a;f(q(a))).
В результате получены две контрарных формулы: P3(b;a;f(q(a))) и P3(b;a;f(q(a))).
Принцип резолюции может быть усилен линейным выводом, упорядочением атомов в дизъюнкте и использованием информации о резольвируемых атомах.
Линейным выводом из множества дизъюнктов K называется последовательность дизъюнктов D1, D2,...Dn, где каждый член DiK, а каждый Di+1 является резольвентой центрального дизъюнкта (или предшествующей резольвенты) и бокового дизъюнкта из множества K.
Упорядоченным дизъюнктом называется дизъюнкт с заданной последовательностью атомов. Атом Pj
Так доказана истинность формулы x(P3(x)(P2(x))).
На рис. 12 приведен граф, иллюстрирующий процесс дедуктивного вывода.
x( P1(x)( P2(x)))
x(P3 (x)P1 (x))


(P1 (t)( P2 (t)))
P3 (t) P1 (t)
(P3 (t)( P2 (t)))
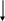
x(P3(x)(P2(x)))
Рис. 12. Граф вывода заключения
Пример: Доказать истинность заключения
 x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))); x(P3(x))
x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))); x(P3(x)) x(P3(x))xy(P21.(x; y)(P2(y))).
1) F1=x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y))) - посылка;
2) F2= x(P3(x)) -посылка;
3) F3=x(P3(x)) - заключение no формуле F2 и правилу 5) смены кванторов (закон де Моргана);
4) F4=P3 (t) - заключение по формуле F3 и правилу 2) удаления квантора общности;
5) F5=P3(t)P24.(x;t) - заключение по формуле F4 и правилу 4) исчисления высказываний;
6) F6=y(P3(y)(P24 (x; y))) - заключение по формуле F5 и правилу 1) введения квантора общности;
7) F7=y(P3(y)P24 (x; y)) - заключение по формуле F6 и правилу смены кванторов (закон де Моргана);
8) F8=y(P21.(t; y)P2(y)y(P3(y)P24.(t; y)) - заключение по формуле F1 и правилу 2) удаления квантора общности;
9) F9= y(P21.(t; y)P2(y)) - заключение пo формулам F7 и F8 при условии t=x и правилу modus tollens;
10) F10=y( P21.(t; y)P2(y)) - заключение по формуле F9 и правилу смены кванторов (закон де Моргана);
11) F11=y(P21. (t; y) (P2
(y)) - заключение пo формуле F10 и эквивалентным преобразованиям алгебры предикатов;
12) F12=xy(P21. (x; y) (P2 (y)) - заключение по формуле F11 и правилу 1) введения квантора общности;
13) x(P3(x))xy(P21.(x; y)( P2(y))) – заключение по формулам F2 и F12 и правилу modus ponens. Что и требовалось доказать.
x(P3(x))
x(y(P21.(x; y)P2(y))y((P3(y) P24.(x; y)))
На рис. 13 приведен граф вывода этой задачи.

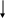
x(P3(x))
y(P21.(t; y)P2(y)y(P3(y)P24.(t; y))
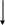




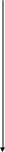
P3 (t)
y(P21.(t; y)P2(y))

P3(t)P24.(x;t)
y( P21.(t; y)P2(y))


y(P21. (t; y) (P2 (y))
y(P3(y)(P24 (x; y)))

y(P3(y)P24 (x; y))
xy(P21. (x; y) (P2 (y))

x(P3(x))xy(P21.(x; y)( P2(y)))

рис. 13 Граф вывода заключения
Пример. Доказать истинность заключения
 x(P1(x)y(P2(y)P24.(x; y))); x(P1(x)y(P3(y)P24.(x; y)))
x(P1(x)y(P2(y)P24.(x; y))); x(P1(x)y(P3(y)P24.(x; y))) x(P2(x)P3(x)).
1) F1=x(P1(x)y(P2(y)P24.(x; y))) - посылка;
2) F2=x(P1(x)y(P3(y)P24 (x; y))) - посылка;
3) F3=P1(а)y(P2(y)P24.(a; y))-заключение по формуле F1, правилу формирования ССФ;
4) F4=P1(a)- заключение по формуле F3 и правилу удаления конъюнкции исчисления высказываний
5) F5=y(P2(y) P24.(a; y)) - заключение пo формуле F3 и правилу удаления конъюнкции исчисления высказываний;
6) F6=P2(t) P24.(a; t) - заключение по формуле F5 и правилу 2) удаления квантора общности;
7) F7=P1(t)y(P3(y)P24 (t; y)) - заключение по формуле F2 и правилу 2) удаления квантора общности;
8) F8=y(P3(y) P24 (a; y)) - заключение по формулам F3 и F7 при t=a и правилу modus ponens;
9) F9=P3(t)P24.(a; t) - заключение по формуле F8 и правилу 2) удаления квантора общности;
10) F10=P24.(a; t)P3(t) - заключение по формуле F9 и закону контрапозиции (правило 8) исчисления высказываний);
11) F11=P2(t)P3(t) - заключение по формулам F6 и F10 и закону силлогизма (правило 11) исчисления высказываний);
12) F12=x( P2 (x)P3(x)) - заключение по формуле F11 и правилу 1) введения квантора x. Что требовалось доказать.
На рис. 14 приведен граф вывода этой задачи.
x(P1(x)y(P2(y)P24 (x; y)))
x(P1(x)y(P3(y)P24.(x; y)))

 x=a
x=aP1(а)y(P2(y)P24.(a; y))
P1(t )y(P3(y)P24 (t; y))


P1(a)
y(P2(y) P24.(a; y))
P1(a )y(P3(y)P24 (a; y))


y(P3(y) P24 (a; y))
P2(t) P24.(a; t)
P3(t)P24.(a; t)
P24.(a; t)P3(t)



P2(t)P3(t)
x( P2 (x)P3(x))
Рис. 14. Граф вывода заключения
2.2.4 Принцип резолюции
Если матрица формулы в результате приведения к виду ПНФ не будет содержать свободных переменных и сколемовских функций, то для вывода заключения полностью пpuменим алгоритм принципа резолюции, рассмотренный в исчислении высказываний. Этот алгоритм основывается на том, что если две формулы состоящие из дизъюнкции атомов (в дальнейшем такие формулы будем называть дизъюнктами ) связаны конъюнкцией, и в них имеются два одинаковых или приводимых к одинаковым (унифицируемых ) атома с разными знаками, то из них можно получить третий дизъюнкт , который будет логическим следствием первых двух, и в нем будут исключены эти два атома. Однако, если в результате приведения к виду ССФ аргументы атомов содержат сколемовские функции, то для поиска контрарных атомов необходимо выполнить подстановки термов вместо предметных переменных и получить новые формулы дизъюнктов, которые допускают их унификацию при формировании контрарных пар. Множество подстановок нужно формировать последовательно, просматривая каждый раз только одну предметную переменную.
Например, если даны два дизъюнкта (P1(x)P2(x)) и (P1(f(x))P3(y)), то для получения контрарной пары атомов возможна подстановка
xf(х)(P1(x)P2(x))=(P1(f(x))P2(f(x))) и
xf(х)(P1(f(x))P3(y))= (P1(f(x))P3(y)).
В результате склеивания этих дизъюнктов может быть получена резольвента: (P1(f(x))P2(f(x)))(P1(f(x))P3(y))= (P2(f(x)) P3(y)).
Если пара дизъюнктов имеет вид (P1(f1(x))P2(x)) и (P1(f2(x))P3(y)), то никакая подстановка не позволит сформировать резольвенту.
Пример: Даны две формулы P3(a;x;f(q(y))) и P3(z;f(z);f(u)).
Выполнить унификацию контрарных атомов.
1) za P3(z;f(z);f(u))=P3(a;f(a);f(u));
2) xf(a) P3(a;x;f(q(y)))=P3(a;f(a);f(q(y)));
3) uq(y) P3(a;f(a);f(u))=P3(a;f(a);f(q(y))).
В результате получены два контрарных атома: P3(a;f(a);f(q(y))) и P3(a;f(a);f(q(y))). Если в эти формулы атомов вместо предметной переменной y сделать подстановку предметной постоянной b, т.е.
ybP3(a;f(a);f(q(y)))=P3(a;f(a);f(q(b))) и
ybP3(a;f(a);f(q(y)))= P3(a;f(a);f(q(b))),
то получим два контрарных высказывания.
Пример. Даны две формулы P3(x;a;f(q(a))) и P3(z;y;f(u)).
Выполнить унификацию контрарных формул.
1) xbP3(x;a;f(q(a)))=P3(b;a;f(q(a)));
2) ya P3(z;y;f(u))=P3(z;a;f(u));
3) yaP3(z;a;f(u))=P3(b;a;f(u));
4) uq(a)P3(b;a;f(u))=P3(b;a;f(q(a))).
В результате получены две контрарных формулы: P3(b;a;f(q(a))) и P3(b;a;f(q(a))).
Принцип резолюции может быть усилен линейным выводом, упорядочением атомов в дизъюнкте и использованием информации о резольвируемых атомах.
Линейным выводом из множества дизъюнктов K называется последовательность дизъюнктов D1, D2,...Dn, где каждый член DiK, а каждый Di+1 является резольвентой центрального дизъюнкта (или предшествующей резольвенты) и бокового дизъюнкта из множества K.
Упорядоченным дизъюнктом называется дизъюнкт с заданной последовательностью атомов. Атом Pj