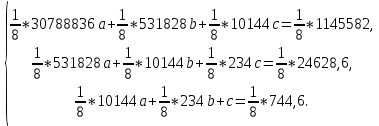
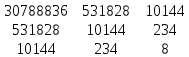
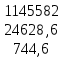
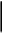
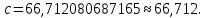
y



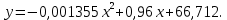
х


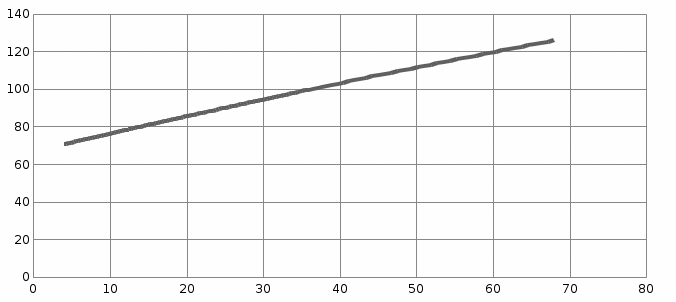
Рис.3.

3.

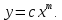
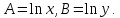
A	1,386	2,303	2,708	3,045	3,367	3,584	3,932	4,22
B	4,263	4,335	4,389	4,451	4,532	4,599	4,733	4,829

---

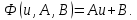
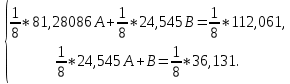
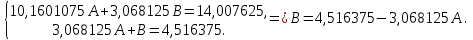
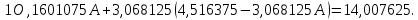
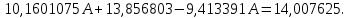
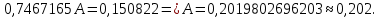
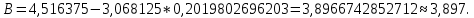
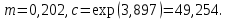
y



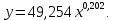
х


Рис.4.


y
4. Объединим для наглядности графики всех функций.


х


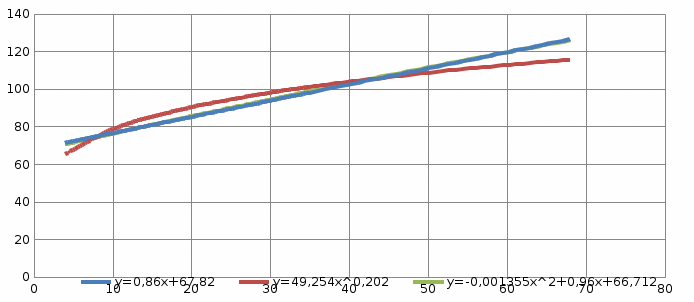
Рис.5.

5. Для сравнения качества приближений вычислим суммы квадратов уклонений.

x	y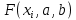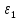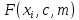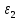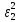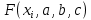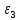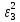
4	71	71,26	0,26	0,0676	65,171	5,829	33,977	70,53	0,47	0,221
10	76,3	76,42	0,12	0,0144	78,423	2,123	4,507	76,177	0,123	0,015
15	80,6	80,72	0,12	0,0144	85,116	4,516	20,394	80,807	0,207	0,043
21	85,7	85,88	0,18	0,0324	91,102	5,402	29,182	86,274	0,574	0,329
29	92,9	92,76	0,14	0,0196	97,24	4,34	18,836	93,412	0,512	0,262
36	99,4	98,78	0,62	0,3844	101,581	2,181	4,757	99,516	0,116	0,013
51	113,6	111,68	1,92	3,6864	108,986	4,614	21,289	112,148	1,452	2,108
68	125,1	126,3	1,2	1,44	115,507	9,593	92,026	125,726	0,626	0,392
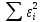		5,6592			224,968			3,383

---

Как следует из таблицы, сумма квадратов уклонений для линейной функции – 5,6592, для степенной – 224,968, для квадратного трёхчлена – 3,383. Сравнивая качество приближений, находим, что приближение в виде квадратного трёхчлена в данном случае предпочтительнее.

---

Смотрите также файлы

• ыса мерзімді саба жоспары Тексерілді.docx

• Основы моральнополитической готовности сотрудников к выполнению поставленных задач по предназначению.doc

• Жусан иісі (Сайын Мратбеков).docx

• Методические указания по выполнению практических и самостоятельных работ для бакалавров направления.docx

• Рефера т История древнего египта Содержание.docx